一行代码击败 100% 用户,leetcode 尼姆问题求解
大家好,我是小浩哥。
记得还是初中时期,就和同学玩过这样一个游戏。和对手轮流从一堆棋子中取走一个或者多个,最后不能再取的就是输家。

多年以后才知道,这一类游戏被称为尼姆游戏,是一种两个人玩的回合制数学战略游戏。
那这一类问题,我们该如何用代码进行求解?
01、题目示例
| 第292题:Nim 游戏 |
|---|
| 你和你的朋友,两个人一起玩 Nim 游戏:桌子上有一堆石头,每次你们轮流拿掉 1 - 3 块石头。拿掉最后一块石头的人就是获胜者。你作为先手。你们是聪明人,每一步都是最优解。编写一个函数,来判断你是否可以在给定石头数量的情况下赢得游戏。 |
示例:
输入: 4
输出: false
解释: 如果堆中有 4 块石头,那么你永远不会赢得比赛;
因为无论你拿走 1 块、2 块 还是 3 块石头,最后一块石头总是会被你的朋友拿走。
02、题目分析
这种问题,如果没有思路,可以先自己找个纸写写画画,找找规律。
首先如果石头数小于 4 个,那么因为你是先手,一把拿走,肯定会赢。
如果石头恰好是 4 个。那不管你是拿了1,2,3个,最后一个都可以被你的对手拿走,所以怎么样都赢不了。这应该是很好理解。

继续分析至 8 个石头:
对于 5、6、7 而言,你只需要对应的拿走 1、2、3,然后留下4个,则对方必输。
但是如果你要面对的是 8,不管先拿(1、2、3)个,另一个人都可以通过 8 - (1、2、3) ,使得你面对 4 个石头,则你必输无疑。
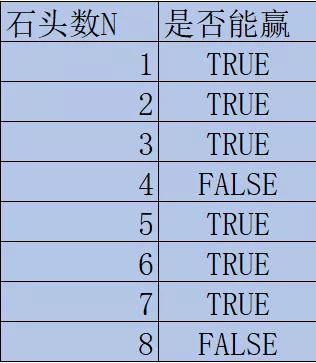
通过观察,我们发现,好像是只要 N 是 4的倍数,我们就必输无疑。
尝试性的写下代码:
//go
func canWinNim(n int) bool {
return n % 4 != 0
}难以想象这么简单:

03、证明过程
首先需要说下的是,这个问题属于博弈论。一个非常典型的尼姆游戏。
回到本题,假若对于先手有N个石头,那么后手的可能性有 N-1,N-2,N-3 三种。只有当后手的这三种可能性都必胜时,N 才会必败。因为题目说了,我是聪明人(博弈论前提条件),那如果后手的三种可能性中,有哪一种必败,作为先手,我们一定会走出这种可能性。那这种可能性是什么,其实就是让对方去面对 4 的倍数。如果先手我们遇到一个不是 4 的倍数的值 x,有:
N 一定处于两个 4 的倍数之间,因为 N 本身不是 4 的倍数,那 N 距离最近的 4 的倍数的值最大为 3。所以,只要我们不是面对 4 的倍数,作为先手,我们一定可以取走(1、2、3),使剩余的值变成 4 的倍数,则后手必输无疑。
欢迎关注微信公众号:互联网全栈架构,收取更多有价值的信息。
