深入浅出聚类分析

1
如何选择聚类分析算法
聚类算法有几十种之多,聚类算法的选择,主要参考以下因素:
如果数据集是高维的,那么选择谱聚类,它是子空间划分的一种。
如果数据量为中小规模,例如在100万条以内,那么K均值将是比较好的选择;
如果数据量超过100万条,那么可以考虑使用Mini Batch KMeans。
如果数据集中有噪点(离群点),那么使用基于密度的DBSCAN可以有效应对这个问题。
如果追求更高的分类准确度,那么选择谱聚类将比K均值准确度更好。
2
KMeans算法
1.原理
K-Means算法的思想很简单,对于给定的样本集,按照样本之间的距离大小,将样本集划分为K个簇。让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大。
如果用数据表达式表示,假设簇划分为(C1,C2,...Ck),则我们的目标是最小化平方误差E:

其中μi是簇Ci的均值向量,有时也称为质心,表达式为:

首先我们看看K-Means算法的一些要点:
(1)对于K-Means算法,首先要注意的是k值的选择,一般来说,我们会根据对数据的先验经验选择一个合适的k值,如果没有什么先验知识,则可以通过交叉验证选择一个合适的k值。
(2)在确定了k的个数后,我们需要选择k个初始化的质心,就像上图b中的随机质心。
由于我们是启发式方法,k个初始化的质心的位置选择对最后的聚类结果和运行时间都有很大的影响,因此需要选择合适的k个质心,最好这些质心不能太近。
好了,现在我们来总结下传统的K-Means算法流程:
(1)输入是样本集D={x1,x2,...xm},聚类的簇树k,最大迭代次数N
(2)输出是簇划分C={C1,C2,...Ck}
(3)从数据集D中随机选择k个样本作为初始的k个质心向量:{μ1,μ2,...,μk}
(4)对于n=1,2,...,N
将簇划分C初始化为Ct=∅t=1,2...k
对于i=1,2...m,计算样本xi和各个质心向量μj(j=1,2,...k)的距离:dij=||xi−μj||22,将xi标记最小的为dij所对应的类别λi。此时更新Cλi=Cλi∪{xi}
对于j=1,2,...,k,对Cj中所有的样本点重新计算新的质心μj=1|Cj|∑x∈Cjx
如果所有的k个质心向量都没有发生变化,则转到步骤3
(5)输出簇划分C={C1,C2,...Ck}
2.代码实例
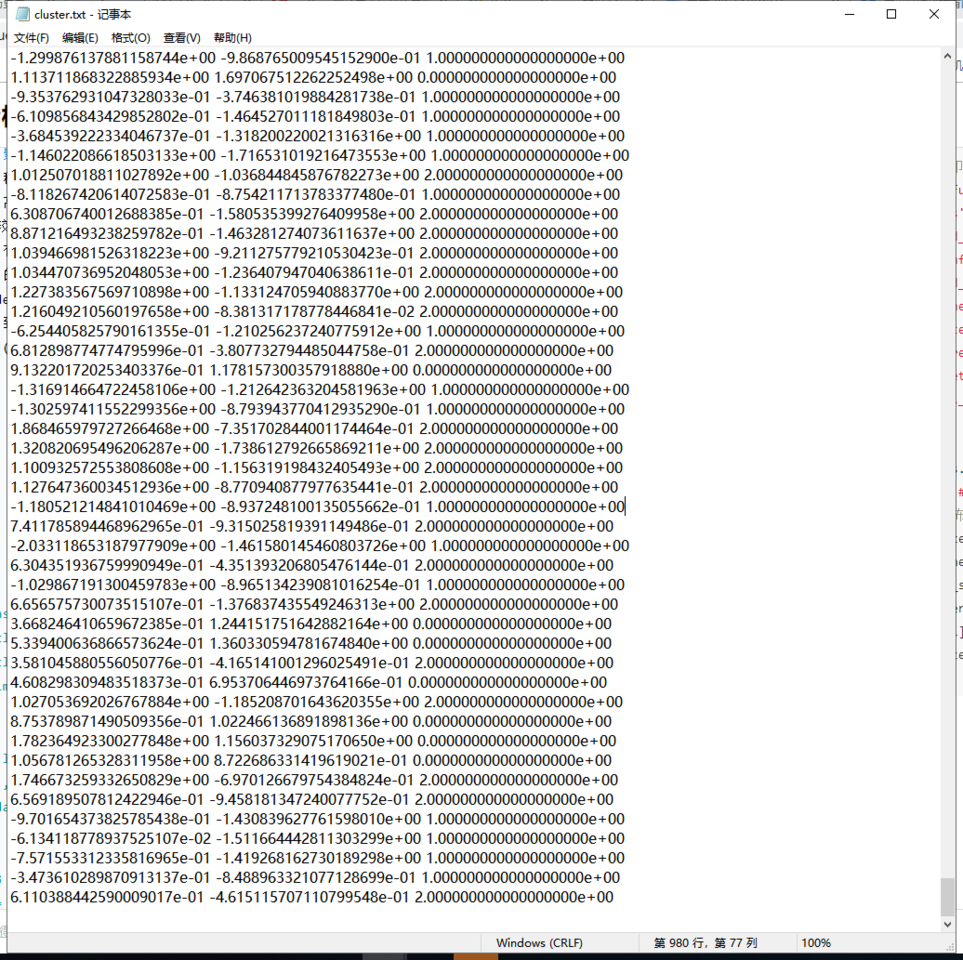
(1)原始数据 Sklearn中有专门的聚类库cluster,在做聚类时只需导入这个库,便可使用其中多种聚类算法,例如K均值、DBSCAN、谱聚类等。
本示例模拟的是对一份没有任何标签的数据集做聚类分析,以得到不用类别的特征和分布状态等,主要使用Sklearn做聚类、用Matplotlib 做图形展示。数据源文件命名为clustring.txt。
(2)代码实现
# 导入库
import numpy as np # 导入numpy库
import matplotlib.pyplot as plt # 导入matplotlib库
from sklearn.cluster import KMeans # 导入sklearn聚类模块
from sklearn import metrics # 导入sklearn效果评估模块
# 数据准备
raw_data = np.loadtxt('./cluster.txt') # 导入数据文件
X = raw_data[:, :-1] # 分割要聚类的数据
y_true = raw_data[:, -1]
# 训练聚类模型
n_clusters = 3 # 设置聚类数量
model_kmeans = KMeans(n_clusters=n_clusters, random_state=0) # 建立聚类模型对象
model_kmeans.fit(X) # 训练聚类模型
y_pre = model_kmeans.predict(X) # 预测聚类模型
# 模型效果指标评估
n_samples, n_features = X.shape # 总样本量,总特征数
inertias = model_kmeans.inertia_ # 样本距离最近的聚类中心的总和
adjusted_rand_s = metrics.adjusted_rand_score(y_true, y_pre) # 调整后的兰德指数
mutual_info_s = metrics.mutual_info_score(y_true, y_pre) # 互信息
adjusted_mutual_info_s = metrics.adjusted_mutual_info_score(y_true, y_pre) # 调整后的互信息
homogeneity_s = metrics.homogeneity_score(y_true, y_pre) # 同质化得分
completeness_s = metrics.completeness_score(y_true, y_pre) # 完整性得分
v_measure_s = metrics.v_measure_score(y_true, y_pre) # V-measure得分
silhouette_s = metrics.silhouette_score(X, y_pre, metric='euclidean') # 平均轮廓系数
calinski_harabaz_s = metrics.calinski_harabaz_score(X, y_pre) # Calinski和Harabaz得分
print('总样本量: %d \t 总特征数: %d' % (n_samples, n_features)) # 打印输出样本量和特征数量
print(70 * '-') # 打印分隔线
print('ine\tARI\tMI\tAMI\thomo\tcomp\tv_m\tsilh\tc&h') # 打印输出指标标题
print('%d\t%.2f\t%.2f\t%.2f\t%.2f\t%.2f\t%.2f\t%.2f\t%d' % (
inertias, adjusted_rand_s, mutual_info_s, adjusted_mutual_info_s, homogeneity_s, completeness_s,
v_measure_s,
silhouette_s, calinski_harabaz_s)) # 打印输出指标值
print(70 * '-') # 打印分隔线
print('简写 \t 全称') # 打印输出缩写和全名标题
print('ine \t 样本距离最近的聚类中心的总和')
print('ARI \t 调整后的兰德指数')
print('MI \t 互信息')
print('AMI \t 调整后的互信息')
print('homo \t 同质化得分')
print('comp \t 完整性得分')
print('v_m \t V-measure得分')
print('silh \t 平均轮廓系数')
print('c&h \t Calinski和Harabaz得分')
# 模型效果可视化
centers = model_kmeans.cluster_centers_ # 各类别中心
colors = ['#4EACC5', '#FF9C34', '#4E9A06'] # 设置不同类别的颜色
plt.figure() # 建立画布
for i in range(n_clusters): # 循环读类别
index_sets = np.where(y_pre == i) # 找到相同类的索引集合
cluster = X[index_sets] # 将相同类的数据划分为一个聚类子集
plt.scatter(cluster[:, 0], cluster[:, 1], c=colors[i], marker='.') # 展示聚类子集内的样本点
plt.plot(centers[i][0], centers[i][1], 'o', markerfacecolor=colors[i], markeredgecolor='k',
markersize=6) # 展示各聚类子集的中心
plt.show() # 展示图像结果:
总样本量: 1000 总特征数: 2
----------------------------------------------------------------------
ine ARI MI AMI homo comp v_m silh c&h
300 0.96 1.03 0.94 0.94 0.94 0.94 0.63 2860
----------------------------------------------------------------------
简写 全称
ine 样本距离最近的聚类中心的总和
ARI 调整后的兰德指数
MI 互信息
AMI 调整后的互信息
homo 同质化得分
comp 完整性得分
v_m V-measure得分
silh 平均轮廓系数
c&h Calinski和Harabaz得分
3. 效果评估
通过不同的指标来做聚类效果评估。
(1)样本距离最近的聚类中心的总和
inertias:inertias是K均值模型对象的属性,表示样本距离最近的聚类中心的总和,它是作为在没有真实分类结果标签下的非监督式评估指标。
该值越小越好,值越小证明样本在类间的分布越集中,即类内的距离越小。
(2)调整后的兰德指数
adjusted_rand_s:调整后的兰德指数(Adjusted Rand Index),兰德指数通过考虑在预测和真实聚类中在相同或不同聚类中分配的所有样本对和计数对来计算两个聚类之间的相似性度量。
调整后的兰德指数通过对兰德指数的调整得到独立于样本量和类别的接近于0的值,其取值范围为[-1,1],负数代表结果不好,越接近于1越好意味着聚类结果与真实情况越吻合。
(3)互信息
mutual_info_s:互信息(Mutual Information,MI),互信息是一个随机变量中包含的关于另一个随机变量的信息量,在这里指的是相同数据的两个标签之间的相似度的量度,结果是非负值。
(4)调整后的互信息
adjusted_mutual_info_s:调整后的互信息(Adjusted MutualInformation,AMI),调整后的互信息是对互信息评分的调整得分。
它考虑到对于具有更大数量的聚类群,通常MI较高,而不管实际上是否有更多的信息共享,它通过调整聚类群的概率来纠正这种影响。
当两个聚类集相同(即完全匹配)时,AMI返回值为1;随机分区(独立标签)平均预期AMI约为0,也可能为负数。
(5)同质化得分
homogeneity_s:同质化得分(Homogeneity),如果所有的聚类都只包含属于单个类的成员的数据点,则聚类结果将满足同质性。
其取值范围[0,1]值越大意味着聚类结果与真实情况越吻合。
(6)完整性得分
completeness_s:完整性得分(Completeness),如果作为给定类的成员的所有数据点是相同集群的元素,则聚类结果满足完整性。
其取值范围[0,1],值越大意味着聚类结果与真实情况越吻合。
(7)V-measure得分
v_measure_s:它是同质化和完整性之间的谐波平均值,v=2*(均匀性*完整性)/(均匀性+完整性)。
其取值范围[0,1],值越大意味着聚类结果与真实情况越吻合。
(8)轮廓系数
silhouette_s:轮廓系数(Silhouette),它用来计算所有样本的平均轮廓系数,使用平均群内距离和每个样本的平均最近簇距离来计算, 是一种非监督式评估指标。
其最高值为1,最差值为-1,0附近的值表示重叠的聚类,负值通常表示样本已被分配到错误的集群。
(9)群内离散与簇间离散的比值
calinski_harabaz_s:该分数定义为群内离散与簇间离散的比值,它是一种非监督式评估指标。
3
基于RFM的用户价值度分析
1.案例背景
用户价值细分是了解用户价值度的重要途径,而销售型公司中对于订单交易尤为关注,因此基于订单交易的价值度模型将更适合运营需求。
对于用户价值度模型而言,由于用户的状态是动态变化的,因此一般需要定期更新,业务方的主要需求是至少每周更新一次。
由于要兼顾历史状态变化,因此在每次更新时都需要保存历史数据,不同时间点下的数据将通过日期区分。
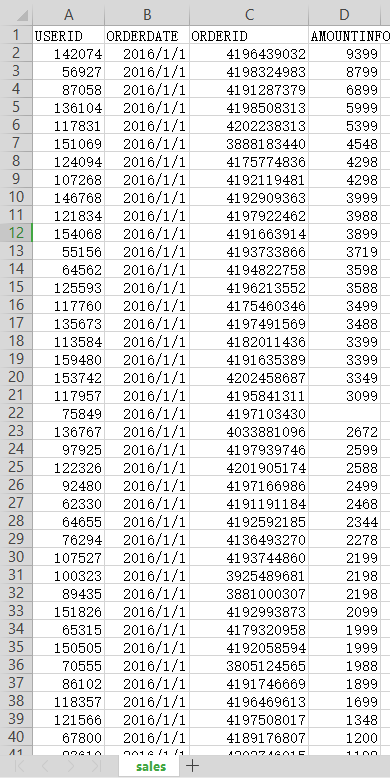
输入源数据score.csv:
2.代码实现
(1)读取数据
# 导入库
import time # 导入时间库
import numpy as np # 导入numpy库
import pandas as pd # 导入pandas库
# 读取数据
dtypes = {'ORDERDATE': object, 'ORDERID': object, 'AMOUNTINFO': np.float32} # 设置每列数据类型
raw_data = pd.read_csv('sales.csv', dtype=dtypes, index_col='USERID') # 读取数据文件
# 数据审查和校验
# 数据概览
print('Data Overview:')
print(raw_data.head(4)) # 打印原始数据前4条
print('-' * 30)
print('Data DESC:')
print(raw_data.describe()) # 打印原始数据基本描述性信息
print('-' * 60)结果:
Data Overview:
ORDERDATE ORDERID AMOUNTINFO
USERID
142074 2016-01-01 4196439032 9399.0
56927 2016-01-01 4198324983 8799.0
87058 2016-01-01 4191287379 6899.0
136104 2016-01-01 4198508313 5999.0
------------------------------
Data DESC:
AMOUNTINFO
count 86127.000000
mean 744.762939
std 1425.194336
min 0.500000
25% 13.000000
50% 59.000000
75% 629.000000
max 30999.000000(2)缺失值审查
# 缺失值审查
na_cols = raw_data.isnull().any(axis=0) # 查看每一列是否具有缺失值
print('NA Cols:')
print(na_cols) # 查看具有缺失值的列
print('-' * 30)
na_lines = raw_data.isnull().any(axis=1) # 查看每一行是否具有缺失值
print('NA Recors:')
print('Total number of NA lines is: {0}'.format(na_lines.sum())) # 查看具有缺失值的行总记录数
print(raw_data[na_lines]) # 只查看具有缺失值的行信息
print('-' * 60)结果:
NA Cols:
ORDERDATE True
ORDERID False
AMOUNTINFO True
dtype: bool
------------------------------
NA Recors:
Total number of NA lines is: 10
ORDERDATE ORDERID AMOUNTINFO
USERID
75849 2016-01-01 4197103430 NaN
103714 NaN 4136159682 189.0
155209 2016-01-01 4177940815 NaN
139877 NaN 4111956196 6.3
54599 2016-01-01 4119525205 NaN
65456 2016-01-02 4195643356 NaN
122134 2016-09-21 3826649773 NaN
116995 2016-10-24 3981569421 NaN
98888 2016-12-06 3814398698 NaN
145951 2016-12-29 4139830098 NaN(3)异常值处理
# 数据异常、格式转换和处理
# 异常值处理
sales_data = raw_data.dropna() # 丢弃带有缺失值的行记录
sales_data = sales_data[sales_data['AMOUNTINFO'] > 1] # 丢弃订单金额<=1的记录
# 日期格式转换
sales_data['ORDERDATE'] = pd.to_datetime(sales_data['ORDERDATE'], format='%Y-%m-%d') # 将字符串转换为日期格式
print('Raw Dtypes:')
print(sales_data.dtypes) # 打印输出数据框所有列的数据类型
print('-' * 60)
# 数据转换
recency_value = sales_data['ORDERDATE'].groupby(sales_data.index).max() # 计算原始最近一次订单时间
frequency_value = sales_data['ORDERDATE'].groupby(sales_data.index).count() # 计算原始订单频率
monetary_value = sales_data['AMOUNTINFO'].groupby(sales_data.index).sum() # 计算原始订单总金额结果:
Raw Dtypes:
ORDERDATE datetime64[ns]
ORDERID object
AMOUNTINFO float32
dtype: object(4)计算RFM得分
# 计算RFM得分
# 分别计算R、F、M得分
deadline_date = pd.datetime(2017, 0o1, 0o1) # 指定一个时间节点,用于计算其他时间与该时间的距离
r_interval = (deadline_date - recency_value).dt.days # 计算R间隔
r_score = pd.cut(r_interval, 5, labels=[5, 4, 3, 2, 1]) # 计算R得分
f_score = pd.cut(frequency_value, 5, labels=[1, 2, 3, 4, 5]) # 计算F得分
m_score = pd.cut(monetary_value, 5, labels=[1, 2, 3, 4, 5]) # 计算M得分
# R、F、M数据合并
rfm_list = [r_score, f_score, m_score] # 将r、f、m三个维度组成列表
rfm_cols = ['r_score', 'f_score', 'm_score'] # 设置r、f、m三个维度列名
rfm_pd = pd.DataFrame(np.array(rfm_list).transpose(), dtype=np.int32, columns=rfm_cols,
index=frequency_value.index) # 建立r、f、m数据框
print('RFM Score Overview:')
print(rfm_pd.head(4))
print('-' * 60)结果:
RFM Score Overview:
r_score f_score m_score
USERID
51220 4 1 1
51221 2 1 1
51224 3 1 1
51225 4 1 1(5)计算RFM总得分
# 计算RFM总得分
# 方法一:加权得分
rfm_pd['rfm_wscore'] = rfm_pd['r_score'] * 0.6 + rfm_pd['f_score'] * 0.3 + rfm_pd['m_score'] * 0.1
# 方法二:RFM组合
rfm_pd_tmp = rfm_pd.copy()
rfm_pd_tmp['r_score'] = rfm_pd_tmp['r_score'].astype(np.str)
rfm_pd_tmp['f_score'] = rfm_pd_tmp['f_score'].astype(np.str)
rfm_pd_tmp['m_score'] = rfm_pd_tmp['m_score'].astype(np.str)
rfm_pd['rfm_comb'] = rfm_pd_tmp['r_score'].str.cat(rfm_pd_tmp['f_score']).str.cat(
rfm_pd_tmp['m_score'])
# 打印输出和保存结果
# 打印结果
print('Final RFM Scores Overview:')
print(rfm_pd.head(4)) # 打印数据前4项结果
print('-' * 30)
print('Final RFM Scores DESC:')
print(rfm_pd.describe())
# 保存RFM得分到本地文件
rfm_pd.to_csv('sales_rfm_score.csv') # 保存数据为csv结果:
Final RFM Scores Overview:
r_score f_score m_score rfm_wscore rfm_comb
USERID
51220 4 1 1 2.8 411
51221 2 1 1 1.6 211
51224 3 1 1 2.2 311
51225 4 1 1 2.8 411
------------------------------
Final RFM Scores DESC:
r_score f_score m_score rfm_wscore
count 59676.000000 59676.000000 59676.000000 59676.000000
mean 3.299970 1.013439 1.000134 2.384027
std 1.402166 0.116017 0.018307 0.845380
min 1.000000 1.000000 1.000000 1.000000
25% 2.000000 1.000000 1.000000 1.600000
50% 3.000000 1.000000 1.000000 2.200000
75% 5.000000 1.000000 1.000000 3.400000
max 5.000000 5.000000 5.000000 5.0000003.效果评估
由于在RFM划分时,将区间划分为5份,因此可以将这5份区间分别定义了:高、中、一般、差和非常差5个级别,分别对应到R、F、M中的5/4/3/2/1。
基于RFM得分业务方得到这样的结论:
公司的会员中99%以上的客户消费状态都不容乐观,主要体现在消费频率低R、消费总金额低M。经过分析,这里主要由于其中有一个用户(ID为74270)消费金额非常高,导致做5分位时收到最大值的影响,区间向大值域区偏移。
公司中有一些典型客户的整个贡献特征明显,重点是RFM得分为555的用户(ID为74270),该用户不仅影响了订单金额高,而且其频率和购买新鲜度和消费频率都非常高,应该引起会员管理部门的重点关注。
本周表现处于一般水平以上的用户的比例(R、F、M三个维度得分均在3以上的用户数)相对上周环比增长了1.3%。这种良好趋势体现了活跃度的提升。
本周低价值(R、F、M得分为111以上)用户名单中,新增了1221个新用户,这些新用户的列表已经被取出。
猜你喜欢
