NetworkX使用手册-技术圈

介绍

NetworkX是一款Python的软件包，用于创造、操作复杂网络，以及学习复杂网络的结构、动力学及其功能。有了NetworkX你就可以用标准或者不标准的数据格式加载或者存储网络，它可以产生许多种类的随机网络或经典网络，也可以分析网络结构，建立网络模型，设计新的网络算法，绘制网络等等。如果在此之前你还不太了解Python，戳这里——>

安装

其实如果要用NetworkX来进行复杂网络的编程还离不开许多相关的其他Python库，我们可以去官网根据需求一一安装，有详细的安装说明。这里推荐一种超级方便实用的方法，即安装Anaconda，Anaconda包含了许多实用的常用Python库，你就不需要再一一自己安装了。请参考。（Anaconda是跨平台的Windows和Linux都支持）

基本使用

（下面实验如果没有特殊说明，都是在Ubuntu下使用Visual Studio Code实验的）

创建一个图首先创建一个空的图
```
import networkx as nx
G = nx.Graph()
```
根据图的定义，一个图包含一个节点集合和一个边集。在NetworkX中，节点可以是任何哈希对象，像一个文本字符串，一幅图像，一个XML对象，甚至是另一个图或任意定制的节点对象。（注意，Python中的None对象是不可以作为节点的类型的。）
节点图G可以通过好几种方式生成。NetworkX包含了许多图的产生函数和一些读写图的工具。我们可以通过一些简单的操作开始最简单的我们一次添加一个节点：
```
`G.add_node(1)`
```
也可以从一个list中添加节点：
```
`G.add_nodes_from([2, 3])`
```
或者从**nbunch**中添加节点，nbunch是任何可迭代的节点容器（如list、set、graph、file等），nbunch本身不是图中的一个节点。
```
H=nx.path_graph(10) #H是一个有10个节点的链状图，即有n个节点n-1条边的连通图
G.add_nodes_from(H) #或者G.add_nodes_from(H.nodes())
```
此时图G中就包含了图H中的10个节点。作为比较，我们可以使图H作为图G的一个节点：
```
`G.add_node(H)`
```
现在图G就包含了一个节点H,即该节点是一个图。可以看到这种灵活性是非常强大的，它允许图的图，文件的图，函数的图等等。因此我们应该好好思考如何构建我们的应用程序才能使我们的节点是有用的实体。当然我们可以在图中使用一个唯一的标识符或者使用一个不同的字典的键来标识节点信息。（如果该hash依赖于它的内容，则我们不应该改变节点对象）
边一个图G可以通过一次添加一条边来构成：
```
G.add_edge(1,2)
```
#等价于
e=(1,2) #e是一个元组 G.add_edge(*e) #这是python中解包裹的过程
也可以通过添加list来添加多条边：
```
G.add_edges_from([(1,2),(1,3)])
```
或者通过添加任何ebunch来添加边，一个ebunch是任何可迭代的边的元组，一个边的元组可以是两个节点之间的一个2元组（无权值的边）或者3元组（3元组还有一个元素是边的权值，比如(1,2,{‘weight’:100})）。下面将进一步讨论边的属性：
```
G.add_edges_from(H.edges()) #不能写作G.add_edges_from(H)
```
我们可以用类似的方法拆除图：G.remove_node(),G.remove_nodes_from(),G.remove_edge(),G.remove_edges_from() 比如：
```
G.remove_node(H)
```
如果你添加的节点和边是已经存在的，是不会报错的。比如，我们先将图G里的所有节点和边删除：
```
G.clear()
```
然后我们新的节点和边，NetworkX会自动忽略掉已经存在的边和节点的添加：
```
G.add_edges_from([(1,2),(1,3)])
G.add_node(1)
G.add_edge(1,2)
G.add_node("spam")       #添加节点"spam"
G.add_nodes_from("spam") #添加节点's' 'p' 'a' 'm'
```
此时图G一共有8个节点和2条边。我们可以通过如下函数查看：
```
print G.number_of_nodes()
print G.number_of_edges()
```
此时对应的网络G的图形为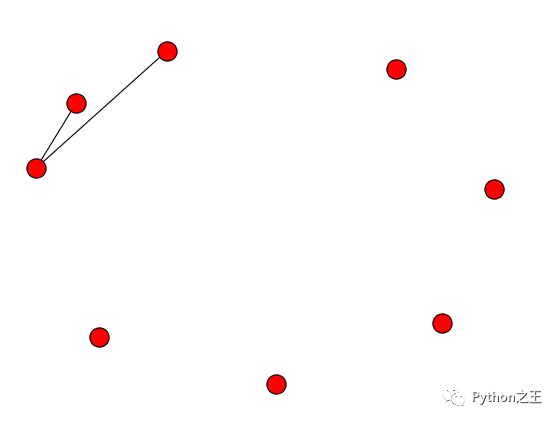：我们还可以查阅当前图G的实际情况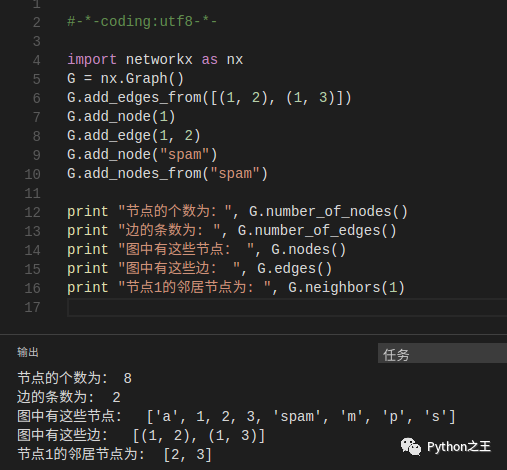：当我们通过某一种图类创建一个图形结构的实例时，我们可以指定好几种不同格式的数据: 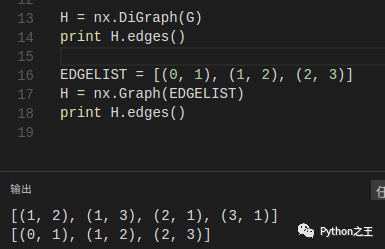可以看到将图G转化为有向图赋给H之后，有向图H由无向图G中的两条无向边转变为4条有向边。后面一个例子是将list直接传到类Graph中，创建由list中的边组成的无向图H。
- 节点和边的使用你可能已经注意到在NetworkX中节点和边并没有被指定一个对象，因此你就可以自由地指定节点和边的对象。最常见的对象是数值和字符串，但是一个节点可以是任意hash对象（除了None对象），一条边也可以关联任意的对象x，比如：G.add_edge(a,b,object=x)。举个关于边关联对象的例子，加入a和b是两个人，而他们两个人之间的联系（边），可以是一个概率，即边的对象是一个概率值，表示这两个人之间每天通电话的可能性。可以看到这是十分强大而且有用的，但是如果你滥用该方法将会导致意想不到的后果，除非你对Python真的很熟悉。如果你不是很确定，你可以考虑使用conver_node_label_to_integers()，他可以将一个图的所有节点按顺序转化为整数对象赋给另一个图。- 访问边除了上面的提到的那些访问节点和边的方法以外（ eg: Graph.nodes(),Graph.edges(),Graph.neighbors()…），当你只是想想要遍历它们时，迭代的版本(eg: Graph.edges_iter())可以省去返回它们时创建如此很大的一个表去存储它们。快速直接的访问图的数据结构可以通过下表来实现。（注意：不要去改变返回的字典，因为它是图数据结构中的一部分，直接的操作可能导致图处于一个不一致的状态。）
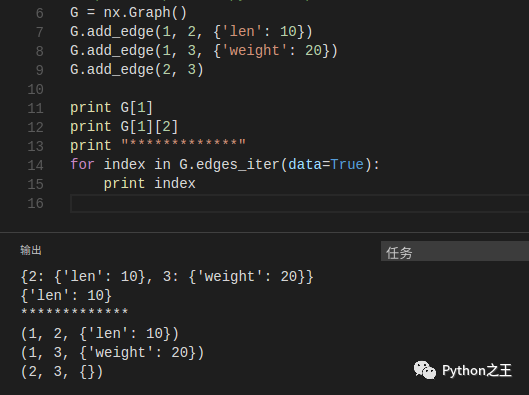
但是我们可以很安全的去改变一条已存在的边的属性（权值）：
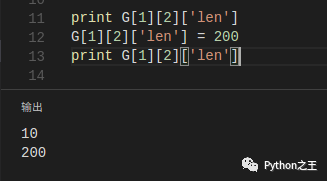
如果想要快速遍历每一条边，我们可以使用邻接迭代器实现，对于无向图，每一条边相当于两条有向边：
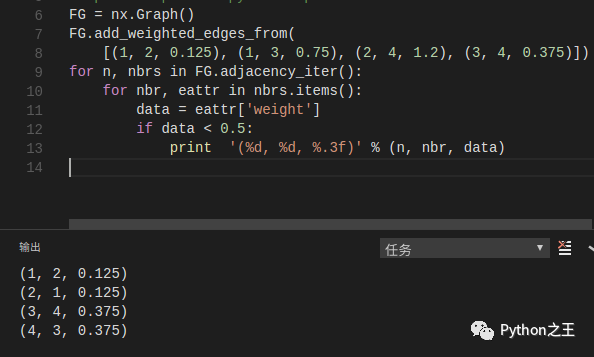
(add_weight_edges_from函数的作用是通过一个ebunch添加一些节点和边，边默认其属性为”weight”) 说明：其实FG.adjacency_iter()返回的是一个所有节点的二元组(node, adjacency dict)的迭代器，比如上述代码中对于节点1返回的是:（1，{2：{0.125}，3：{0.75}}）。一种方便的访问所有边的方法:
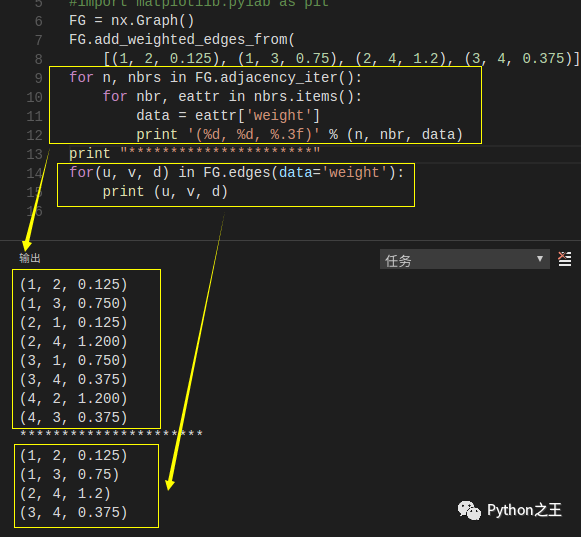
给图、节点和边添加属性属性诸如weight,labels,colors,或者任何对象，你都可以附加到图、节点或边上。对于每一个图、节点和边都可以在关联的属性字典中保存一个（多个）键-值对。默认情况下这些是一个空的字典，但是我们可以增加或者是改变这些属性通过使用add_edge,add_node或者字典操作这些属性字典，比如G.graph,G.node或者G.edge。
- 通过读取存储在文件中的一些标准图形格式，例如边表，邻接表，GML，GraphML，pickle，LEAD或者其他的一些格式：
- 使用随机图发生器
- 使用一些图形生成器
- 使用典型的图形操作：subgraph(G, nbunch) - 产生nbunch节点的子图 union(G1,G2) - 结合图 disjoint_union(G1,G2) - 假设所有节点都不同，然后结合图 cartesian_product(G1,G2) - 返回笛卡尔乘积图 compose(G1,G2) - 结合两个图并表示两者共同的节点 complement(G) - 图G的补图 create_empty_copy(G) - 返回同一类图的无边副本 convert_to_undirected(G) - 返回G的无向图 convert_to_directed(G) - 返回G的有向图- 调用经典的小图
- - 图的属性可以在创建图时分配图的属性：
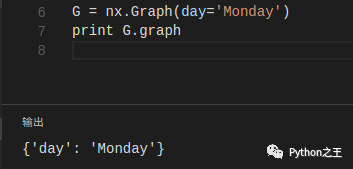
- 你也可以修改已有的属性：
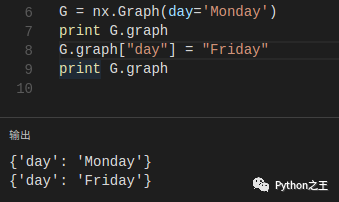
- 你也可以随时添加新的属性到图中：
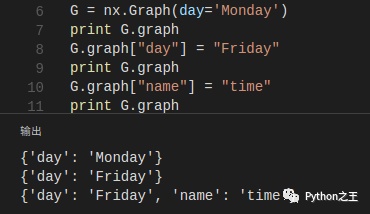
- - 节点的属性通过add_node(),add_nodes_from给节点添加属性或者G.node[][]来修改属性（前面两种在添加的是已存在的节点时，也可以看做是修改节点属性）：
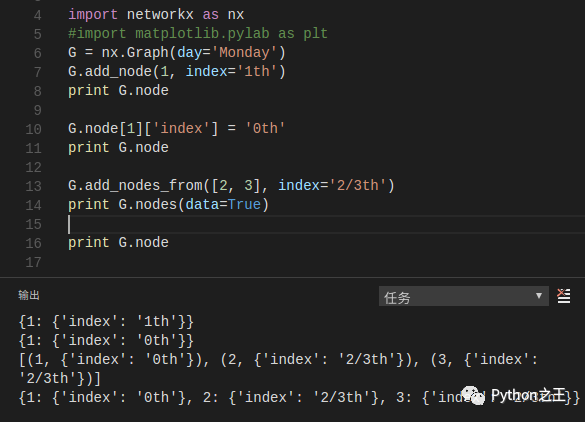
- 注意添加一个节点是G.add_node而不是G.node。- 边点的属性通过add_edge(),add_edges_from()来添加边的属性,下表或者G.edge[][][]来修改属性。
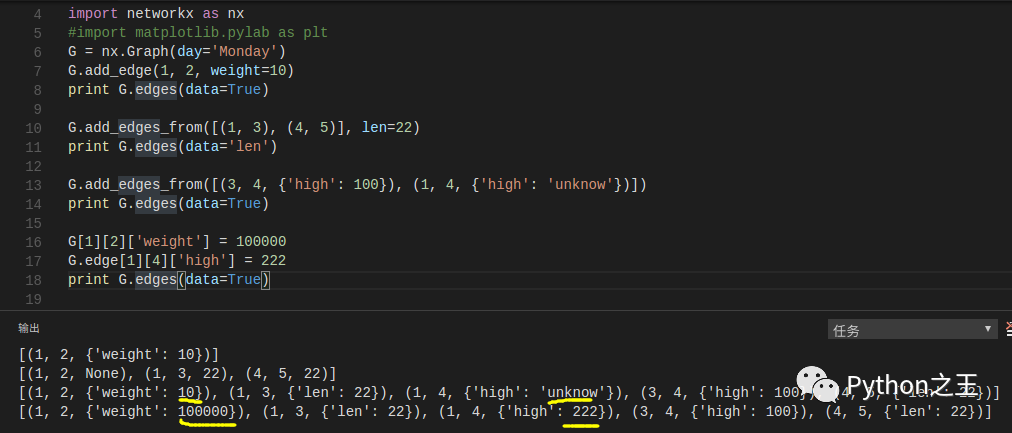
- 注意：注意什么时候使用‘=’，什么时候使用‘:’；什么时候有引号什么时候没有引号。特殊属性weight应该是一个数值型的，并且在算法需要使用weight时保存该数值。有向图 DiGraph类提供了许多有向图中的额外算法，比如DiGraph.out_edges(),DiGraph.in_degree(),DiGraph.predecessors(),DiGraph.successors()等。为了让算法可以在两类图中都可以工作，无向图中的neighbors()和degree()分别等价于有向图中的successors()和有向图中的in_degree()和out_degree()的和。虽然这样有时候会让我们感觉不太一致。

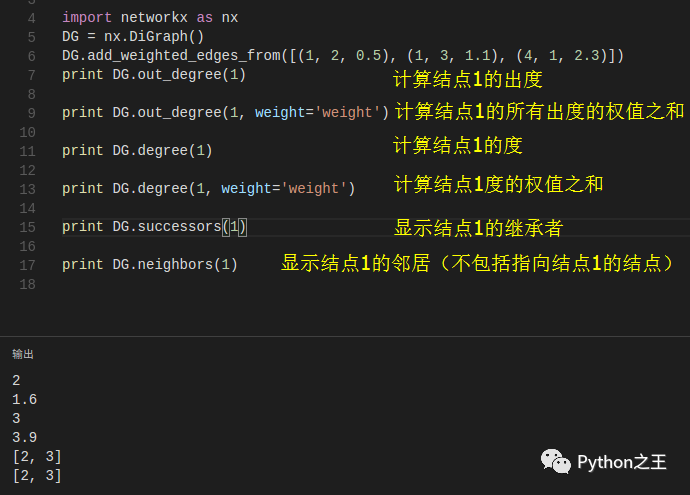
有些算法只能在有向图中使用，而有些图并没有为有向图定义。确实将有向图和无向图混在在一起是很危险的一件事情，所以，如果有些实验你想把一个有向图看做一个无向图，你可以将有向图转化为无向图，通过：

H=DG.to_undirected()

#或者

H=nx.Graph(DG)

多图(Multigraphs) NetworkX提供了一个类，它可以允许任何一对节点之间有多条边。类MultiGraph和类MultiDiGraph允许添加相同的边两次，这两条边可能附带不同的权值。对于有些应用程序这是非常有用的类，但是许多算法不能够很好的在这样的图中定义，比如最短路径算法，但是像MultiGraph.degree这种算法又可以很好的被定义。否则你应该为了很好的定义测量，而将图转化为标准的图。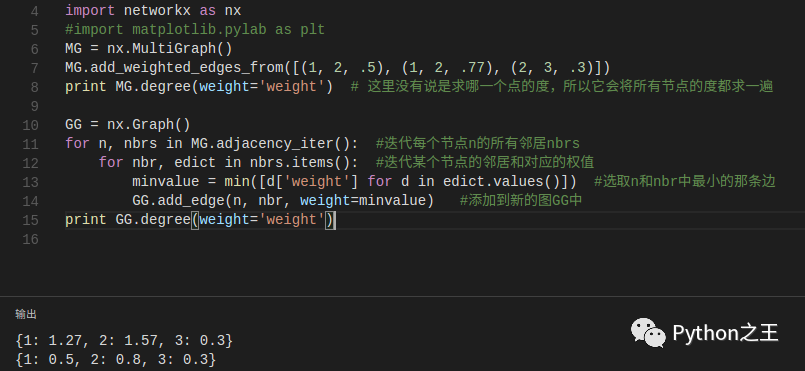

图的生成器和图的操作除了通过节点和边生成图，也可以通过以下方法产生：

petersen=nx.petersen_graph()
tutte=nx.tutte_graph()
maze=nx.sedgewick_maze_graph()
tet=nx.tetrahedral_graph()

K_5=nx.complete_graph(5)
K_3_5=nx.complete_bipartite_graph(3,5)
barbell=nx.barbell_graph(10,10)
lollipop=nx.lollipop_graph(10,20)

er=nx.erdos_renyi_graph(100,0.15)
ws=nx.watts_strogatz_graph(30,3,0.1)
ba=nx.barabasi_albert_graph(100,5)
red=nx.random_lobster(100,0.9,0.9)

nx.write_gml(red,"path.to.file")
mygraph=nx.read_gml("path.to.file")

详细的图的格式请参考官网：详细的图的产生函数请参考官网：

分析图图G的结构可以通过各种图论的函数来分析，例如：

&gt;&gt;&gt; G=nx.Graph()
&gt;&gt;&gt; G.add_edges_from([(1,2),(1,3)])
&gt;&gt;&gt; G.add_node("spam")       # adds node "spam"

&gt;&gt;&gt; nx.connected_components(G)
[[1, 2, 3], ['spam']]

&gt;&gt;&gt; sorted(nx.degree(G).values())
[0, 1, 1, 2]

&gt;&gt;&gt; nx.clustering(G)
{<!-- -->1: 0.0, 2: 0.0, 3: 0.0, 'spam': 0.0}

返回节点属性的函数是通过返回一个以节点为键的字典来实现的：

&gt;&gt;&gt; nx.degree(G)
{1: 2, 2: 1, 3: 1, 'spam': 0}

对于一些特定节点的值，我们可以提供该特定节点（集）的nbunch作为函数参数。如果被指定的是单个节点，则返回一个对应的单一的值，如果被指定的是一个nbunch,则返回一个字典：

&gt;&gt;&gt; nx.degree(G,1)
2
&gt;&gt;&gt; G.degree(1)
2
&gt;&gt;&gt; G.degree([1,2])
{<!-- -->1: 2, 2: 1}
&gt;&gt;&gt; sorted(G.degree([1,2]).values())
[1, 2]
&gt;&gt;&gt; sorted(G.degree().values())
[0, 1, 1, 2]

绘制图 NetworkX并不是专门用来绘图的包，但是Matplotlib以及一些接口却提供了很好的绘图功能。Python3.0以上的版本可能不能很好的兼容NetworkX中的绘图包。

首先我们导入Matplotlib的plot接口（pylab也可以）

import matplotlib.pyplot as plt

#或者

import matplotlib.pylab as plt

你可能会发现使用“ipthon -pylab”q去交互测试代码是很有用的，它提供了强大的ipython和matplotlib，也提供了一个方便的交互模式。

测试networkx.drawing是是否导入成功，可以通过：

nx.draw(G)
nx.draw_random(G)
nx.draw_circular(G)
nx.draw_spectral(G)

你要将这个图形绘制到屏幕，你可能需要Matplotlib:

plt.show()

如果你不需要显示，那你可以将图像保存到一个文件：

nx.draw(G)
plt.savefig("path.png")

最基础的NetworkX的介绍和使用说明到这里就先结束了，后期还会继续学习更深入的NetworkX和复杂网络相结合的相关用法。

Python“宝藏级”公众号【Python之王】专注于Python领域，会爬虫，数分，C++，tensorflow和Pytorch等等。

近 2年共原创 100+ 篇技术文章。创作的精品文章系列有：

Python从入门到大师
Python爬虫专栏
数据分析
机器学习
AI基础

日常收集整理了一批不错的 Python 学习资料，有需要的小伙可以自行免费领取。

获取方式如下：公众号回复资料。领取Python等系列笔记，项目，书籍，直接套上模板就可以用了。资料包含算法、python、算法小抄、力扣刷题手册和 C++ 等学习资料！