人有悲欢离合,月有阴晴圆缺【GLSL】
原文链接: https://juejin.cn/post/7005904041448308749
效果图(静图+动图)

注意:建议在手机 app 端看动图,PC 浏览器上压缩得没法看

虽人有悲欢离合,月有阴晴圆缺,此事古难全。但愿各位读者在中秋佳节来临之际,身边都能有亲人相伴。即使独在异乡为异客,在学习工作之余,也都要平安健康,这样才能与他/她们一起共享这美好的月光。
思路与对应着色器代码
一、构造球体
首先我们以屏幕中心为原点构造三维的坐标
vec3 pos = vec3(fragCoord.xy - iResolution.xy / 2.0, 0.0);
然后依照球体的公式进行计算
float z = r * r - dot(pos, pos);
得到如下所示的效果

为了之后对球内外层的大气光晕做效果,所以我们需要在这里先将球内层和球外层的 z 坐标范围区分出来
float z_in = z > 0. ? sqrt(z) : eps;
float z_out = z < 0. ? sqrt(-z) : -eps;
球内层效果如下(为了方便可视化,对值进行了一些处理):

函数示意图如下:
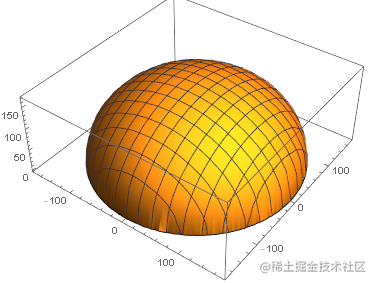
球外层效果如下:

函数示意图如下:
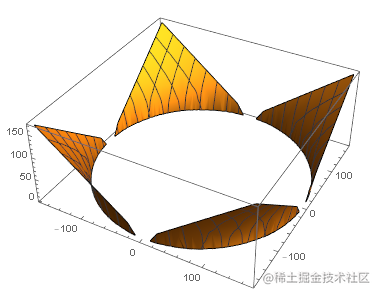
二、营造月球表面的凹凸感
有了球内层的 z 坐标范围,我们就可以构造出它的法线向量
vec3 norm = vec3(0.);
/// @note 法线
if (z_in > eps)
norm = normalize(vec3(pos.x, pos.y, z_in)); ///< 球内层的法线
可视化后的效果如下所示

接下来我们对它进一步的扰动,来营造出月球表面的 “凹凸感”
float nx = fbm(vec3(norm.x + e, norm.y, norm.z )) * 0.5 + 0.5; // x 方向上的法线置换
float ny = fbm(vec3(norm.x, norm.y + e, norm.z )) * 0.5 + 0.5; // y 方向上的法线置换
float nz = fbm(vec3(norm.x, norm.y, norm.z + e)) * 0.5 + 0.5; // z 方向上的法线置换
norm = normalize(norm * vec3(nx, ny, nz));
则我们可以得到如下所示的法线效果

这张图可能效果不是很明显,那么就让我们来看看变换前后的法线向量之差的效果(为了可视化适当的放大):

加了光照的效果则更明显一些(静图+动图)


FBM 噪声的妙用
在营造 “凹凸感” 那节中用到了 Simplex 噪声的 FBM 叠加,来营造月球表面的凹凸感 相关的函数定义如下:
float noise3D(vec3 p)
{
...
}
float simplex3D(vec3 p)
{
...
}
float fbm(vec3 p)
{
...
}
由于它代码量较多,限于篇幅,噪声的详细相关介绍可以参考我的另一篇文章 《ShaderJoy —— 噪声之美,大家一起 “噪” 起来 【GLSL】》
该噪声除了用于以上,还被用于制作月球表面的固有色
/// @note 进一步根据(扰动过的)法线得到月球表面的纹理
float n = 1.0 - (fbm(norm) * 0.5 + 0.5);
其效果如下:

大气的氤氲光晕
通过对球内层和球外层的 z 坐标范围取倒数来实现该效果
/// @note 大气
float z_in_atm = (r * in_outer) / z_in - in_inner; ///< 内层
float z_out_atm = (r * out_inner) / z_out - out_outer; ///< 外层
z_in_atm = max(0.0, z_in_atm);
z_out_atm = max(0.0, z_out_atm);
其中大气氤氲光晕的强度定义如下
/// @note 内外围大气光晕强度
float in_inner = 0.2;
float in_outer = 0.2;
float out_inner = 0.2;
float out_outer = 0.4;
其中内层和外层的光晕效果分别如下所示:

函数示意图如下:
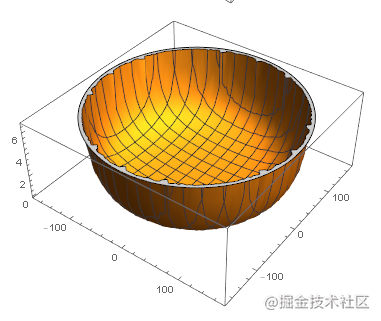

函数示意图如下:
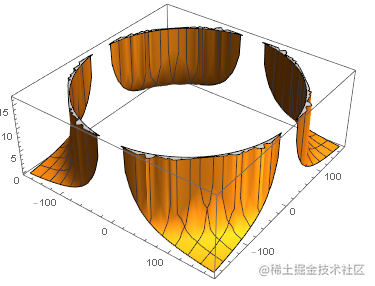
光照的计算
这里的光照计算相当简单,仅仅是将法线和光照方向的点乘计算出的散射光,只不过大气的内外层都需要算一次,还有一次是球体本身的光照计算。
/// @note Diffuse 光照计算
float diffuse = max(0.0, dot(norm, l));
float diffuse_out = max(0.0, dot(norm_out, l) + 0.3);
...
... = n * diffuse ...
为了让月球产生 “阴晴圆缺” 的效果,我们让光照方向随时间而变化,即
// @note 光线 3D 方向向量
vec3 l = normalize(vec3(sin(time), sin(time * 0.5), (cos(time))));
综合起来,光照计算代码如下
fragColor = vec4(vec3(n * diffuse +
z_in_atm * diffuse +
z_out_atm * diffuse_out), 1.0);
至此,我们就得到了开头的效果

完整代码
#define time iTime
/// @note 内外围大气光晕强度
float in_inner = 0.2;
float in_outer = 0.2;
float out_inner = 0.2;
float out_outer = 0.4;
/// -------------------- FBM 噪声相关 --------------------
float noise3D(vec3 p)
{
return fract(sin(dot(p, vec3(12.9898, 78.233, 128.852))) * 43758.5453) * 2.0 - 1.0;
}
float simplex3D(vec3 p)
{
float f3 = 1.0 / 3.0;
float s = (p.x + p.y + p.z) * f3;
int i = int(floor(p.x + s));
int j = int(floor(p.y + s));
int k = int(floor(p.z + s));
float g3 = 1.0 / 6.0;
float t = float((i + j + k)) * g3;
float x0 = float(i) - t;
float y0 = float(j) - t;
float z0 = float(k) - t;
x0 = p.x - x0;
y0 = p.y - y0;
z0 = p.z - z0;
int i1, j1, k1;
int i2, j2, k2;
if (x0 >= y0)
{
if (y0 >= z0)
{
i1 = 1; // X Y Z order
j1 = 0;
k1 = 0;
i2 = 1;
j2 = 1;
k2 = 0;
}
else if (x0 >= z0)
{
i1 = 1; // X Z Y order
j1 = 0;
k1 = 0;
i2 = 1;
j2 = 0;
k2 = 1;
}
else
{
i1 = 0; // Z X Z order
j1 = 0;
k1 = 1;
i2 = 1;
j2 = 0;
k2 = 1;
}
}
else
{
if (y0 < z0)
{
i1 = 0; // Z Y X order
j1 = 0;
k1 = 1;
i2 = 0;
j2 = 1;
k2 = 1;
}
else if (x0 < z0)
{
i1 = 0; // Y Z X order
j1 = 1;
k1 = 0;
i2 = 0;
j2 = 1;
k2 = 1;
}
else
{
i1 = 0; // Y X Z order
j1 = 1;
k1 = 0;
i2 = 1;
j2 = 1;
k2 = 0;
}
}
float x1 = x0 - float(i1) + g3;
float y1 = y0 - float(j1) + g3;
float z1 = z0 - float(k1) + g3;
float x2 = x0 - float(i2) + 2.0 * g3;
float y2 = y0 - float(j2) + 2.0 * g3;
float z2 = z0 - float(k2) + 2.0 * g3;
float x3 = x0 - 1.0 + 3.0 * g3;
float y3 = y0 - 1.0 + 3.0 * g3;
float z3 = z0 - 1.0 + 3.0 * g3;
vec3 ijk0 = vec3(i, j, k);
vec3 ijk1 = vec3(i + i1, j + j1, k + k1);
vec3 ijk2 = vec3(i + i2, j + j2, k + k2);
vec3 ijk3 = vec3(i + 1, j + 1, k + 1);
vec3 gr0 = normalize(vec3(noise3D(ijk0), noise3D(ijk0 * 2.01), noise3D(ijk0 * 2.02)));
vec3 gr1 = normalize(vec3(noise3D(ijk1), noise3D(ijk1 * 2.01), noise3D(ijk1 * 2.02)));
vec3 gr2 = normalize(vec3(noise3D(ijk2), noise3D(ijk2 * 2.01), noise3D(ijk2 * 2.02)));
vec3 gr3 = normalize(vec3(noise3D(ijk3), noise3D(ijk3 * 2.01), noise3D(ijk3 * 2.02)));
float n0 = 0.0;
float n1 = 0.0;
float n2 = 0.0;
float n3 = 0.0;
float t0 = 0.5 - x0 * x0 - y0 * y0 - z0 * z0;
if (t0 >= 0.0)
{
t0 *= t0;
n0 = t0 * t0 * dot(gr0, vec3(x0, y0, z0));
}
float t1 = 0.5 - x1 * x1 - y1 * y1 - z1 * z1;
if (t1 >= 0.0)
{
t1 *= t1;
n1 = t1 * t1 * dot(gr1, vec3(x1, y1, z1));
}
float t2 = 0.5 - x2 * x2 - y2 * y2 - z2 * z2;
if (t2 >= 0.0)
{
t2 *= t2;
n2 = t2 * t2 * dot(gr2, vec3(x2, y2, z2));
}
float t3 = 0.5 - x3 * x3 - y3 * y3 - z3 * z3;
if (t3 >= 0.0)
{
t3 *= t3;
n3 = t3 * t3 * dot(gr3, vec3(x3, y3, z3));
}
return 96.0 * (n0 + n1 + n2 + n3);
}
float fbm(vec3 p)
{
float f;
f = 0.50000 * (simplex3D( p )); p = p * 2.01;
f += 0.25000 * (simplex3D( p )); p = p * 2.02;
f += 0.12500 * (simplex3D( p )); p = p * 2.03;
f += 0.06250 * (simplex3D( p )); p = p * 2.04;
f += 0.03125 * (simplex3D( p )); p = p * 2.05;
f += 0.015625 * (simplex3D( p ));
return f;
}
/// -------------------- FBM 噪声相关 --------------------
/// @note 月球半径
/// r 默认值为 iResolution.y / 3.0
#iUniform float r = 170. in {0., 512.}
/// @note 控制月球表面凹凸感
#iUniform float e = 0.05 in {0., .6}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec3 pos = vec3(fragCoord.xy - iResolution.xy / 2.0, 0.0); // 以屏幕中心为原点
// @note 光线 3D 方向向量
vec3 l = normalize(vec3(sin(time), sin(time * 0.5), (cos(time))));
/// @note 球体并区分内外
float eps = 1e-3;
float z = r * r - dot(pos, pos);
float z_in = z > 0. ? sqrt(z) : eps;
float z_out = -z > 0. ? sqrt(-z) : -eps;
/// @note 法线
vec3 norm = vec3(0.);
vec3 norm_out = vec3(0.);
if (z_in > eps)
norm = normalize(vec3(pos.x, pos.y, z_in)); ///< 球上的法线
// if (z_out > sqrt(e))
norm_out = normalize(vec3(pos.x, pos.y, z_out)); ///< 球外的法线
/// @note 营造凹凸感
float nx = fbm(vec3(norm.x + e, norm.y, norm.z )) * 0.5 + 0.5; // x 方向上的法线置换
float ny = fbm(vec3(norm.x, norm.y + e, norm.z )) * 0.5 + 0.5; // y 方向上的法线置换
float nz = fbm(vec3(norm.x, norm.y, norm.z + e)) * 0.5 + 0.5; // z 方向上的法线置换
norm = normalize(norm * vec3(nx, ny, nz));
/// @note 根据法线得到的噪声纹理
float n = 1.0 - (fbm(norm) * 0.5 + 0.5);
/// @note 大气
float z_in_atm = (r * in_outer) / z_in - in_inner; // 内光晕
float z_out_atm = (r * out_inner) / z_out - out_outer; // 外光晕
z_in_atm = max(0.0, z_in_atm);
z_out_atm = max(0.0, z_out_atm);
// @note Diffuse 光照计算
float diffuse = max(0.0, dot(norm, l));
float diffuse_out = max(0.0, dot(norm_out, l) + 0.3);
/// @note 总体光照
fragColor = vec4(vec3(n * diffuse +
z_in_atm * diffuse +
z_out_atm * diffuse_out), 1.0);
}
-- END --
推荐:
