算法工程师到底是做什么的？

大数据文摘授权转载自龙心辰

作者：龙心辰

其实这是一个不太好解释的问题，因为并没有一个完备的定义。

笔者在算法领域遇到了不少同行，发现各自的工作重点甚至思维方式都很不同。

为了给入门的朋友一个清晰的梳理，这里就简单串一串12个常见的算法。

首先，全景图镇楼。

01 算法与非算法的区别

一般来说，可以把编程工作分为两种，一种是面向实现的，一种是面向优化的。

前者如实现一个功能、搭建一个服务、实现一种展现交互方式等。更关注的是如何实现功能，如何对于各种复杂甚至小众的场景都不出错。互联网中典型的后端、前端、平台、网络工程师的主要工作是这一类。

如果一些功能已经实现了，你主要需要优化它，那这类工作一般比较偏向算法。

其中一个关键是你的优化目标要是客观可量化的。比如一些代码优化的工作是提升代码的可维护性、可读性和可扩展性。

这个优化目标具备比较强的主观性，难以形成量化的指标，属于设计模式主要关注的问题，一般不纳入算法范畴。

另一个区分算法与非算法工作的重要特征是一般涉及数学知识较多的编程工作更偏向算法。

比如对于面向优化的编程工作，为了很好地衡量可量化的目标，其数学定义往往比较明确，相应引入的数学知识会比较多。

那么如果面向实现的编程工作也依赖大量数学知识时是否算作算法呢？

其中一个例子是可计算性理论，它涉及到可判定性问题、数理逻辑等问题都需要大量复杂的数学知识。

这种情况下，它其实更关心何种问题原则上是否可用算法解决，在实际工程领域中并没有大量的岗位与之相匹配，所以本文暂不将其纳入算法工程师考虑的范围。

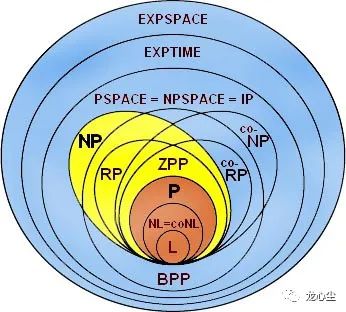
另一个例子是加密算法。加密算法的目标是保证数据的安全通信，保证其加密性、完整性和身份唯一确认。

看起来是面向实现的。但换一个视角，加密算法设计的指导思想是提高其解密成本，也可以算是面向优化的。

02 不同种类算法之间的区别

如果你的优化目标是要降低程序的时间复杂度与空间复杂度，它们都是能够比较严格地量化定义的，就属于经典的“数据结构与算法”中关注的“算法”的问题。

LeetCode中大部分Algorithm的题目都属于此类，也是互联网面试中的高频考点，如常见的分治、递归、动态规划等。

在实际工作中，特别是一些架构师相关的角色，会着重关注这类问题，比如提升增删改查的速度、降低其内存消耗等。相应的数学理论是计算复杂性理论，依赖的数学知识包括离散数学、组合数学、图论等。

如果你的优化目标是要降低在未见过的case上的预测误差，这是典型的机器学习中的算法问题。

这里面涉及到一些核心的概念，包括：泛化误差、训练误差、过拟合、欠拟合、偏差等。相应的算法岗位非常多，图像算法、语音算法、自然语言处理算法、搜索推荐算法等。

机器学习算法还可以根据优化目的的不同进行进一步的细分。如果训练数据带有标签，优化目标是降低预测标签的误差则是最常见的有监督学习。如果训练数据不带标签，则是无监督学习。而如果此时又非要预测对应的标签，则有降维和聚类两种算法。如果仅仅是为了拟合训练数据的分布，那就是生成式算法。

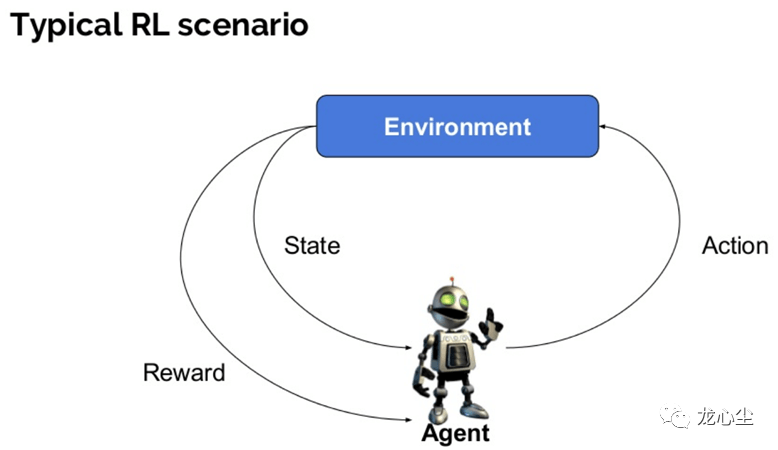
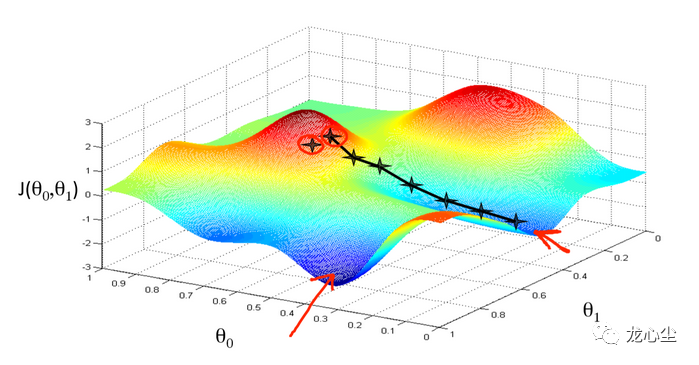
机器学习算法的数学理论是计算学习理论，依赖的数学知识包括概率与统计、最优化理论、线性代数与矩阵论等。

当然，最优化本身就是一种算法。稍微严格一点的表述是在一定的约束条件下控制自变量达到目标函数最优的问题。

最优化问题也叫作运筹学，在工程界应用非常广泛。典型的如外卖骑手调度、网约车调度、航班调度、物流路径调度、广告/补贴金额投放等。

最优化算法的种类也比较多，以自变量是否连续可分为连续最优化和组合优化。很多计算复杂度优化算法可以看做一种广义的组合优化问题。

机器学习算法一般是连续最优化问题。

03 不同算法思路的相互组合

其他一些的高阶算法可以理解为以上多种算法的组合。

比如强化学习算法可以理解成有监督学习算法与最优化决策算法的组合。

也就是智能体根据其对当前环境下长期最大收益进行决策（最优化），而这个收益的函数是需要通过大量样本统计（有监督学习）才能得到，并且智能体的当下决策往往影响周围的环境状态进而进一步影响下一步自身的决策。

其典型应用场景是基于用户实时行为的个性化推荐与搜索，外卖骑手路径优化与订单分配的在线优化等。其实，“强人工智能”如果可行的话，强化学习是其绕不开的学习思路。

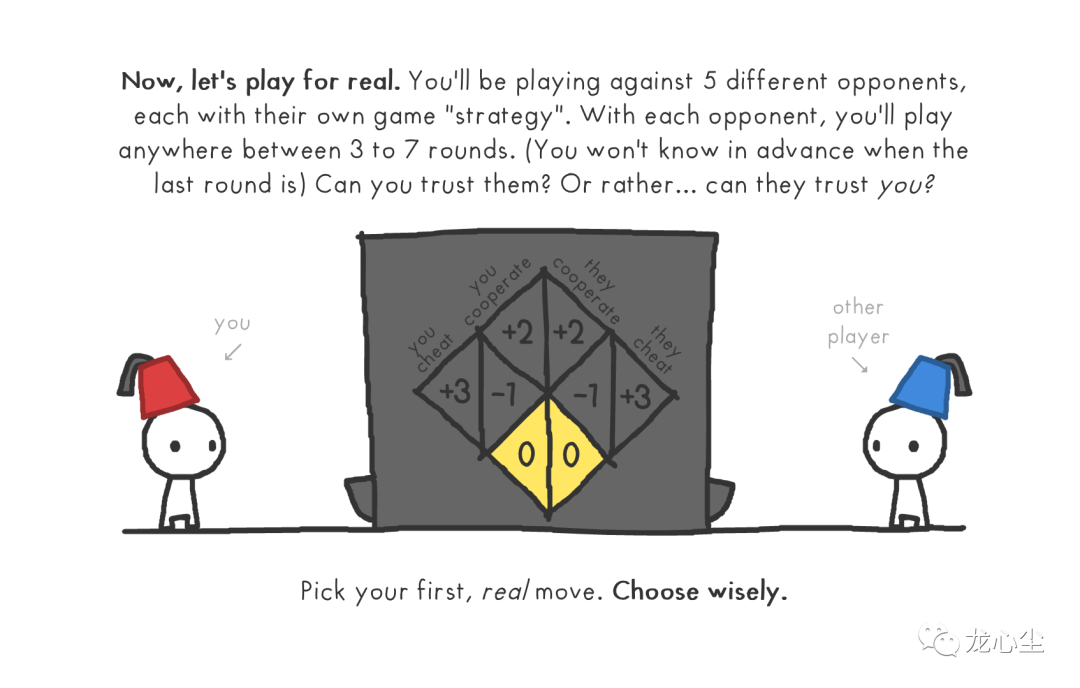
以上介绍的优化算法都是基于单智能体的，而博弈论就将其拓展到多个智能体的最优化，视野一下就打开了。

多个智能体的优化策略是会相互影响的。也就是说它们各自基于自身的优化函数进行优化，并且各自的优化行动可以影响其他智能体优化策略的过程。

博弈论算法典型的应用场景是拍卖竞价策略。

在ACG文化中的《大逃杀》、《赌博默示录》、《弥留之国的爱丽丝》甚至《JOJO》等作品中都充满了大量的博弈论场景。有一个小程序的游戏叫作《信任的进化》，简单玩一下就能够体会到博弈论的有趣之处。

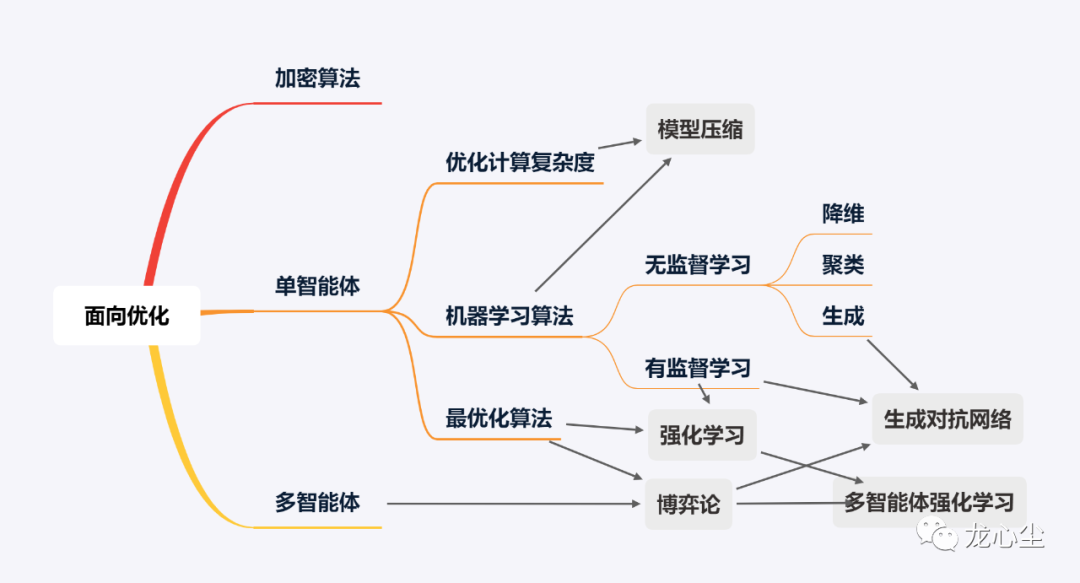
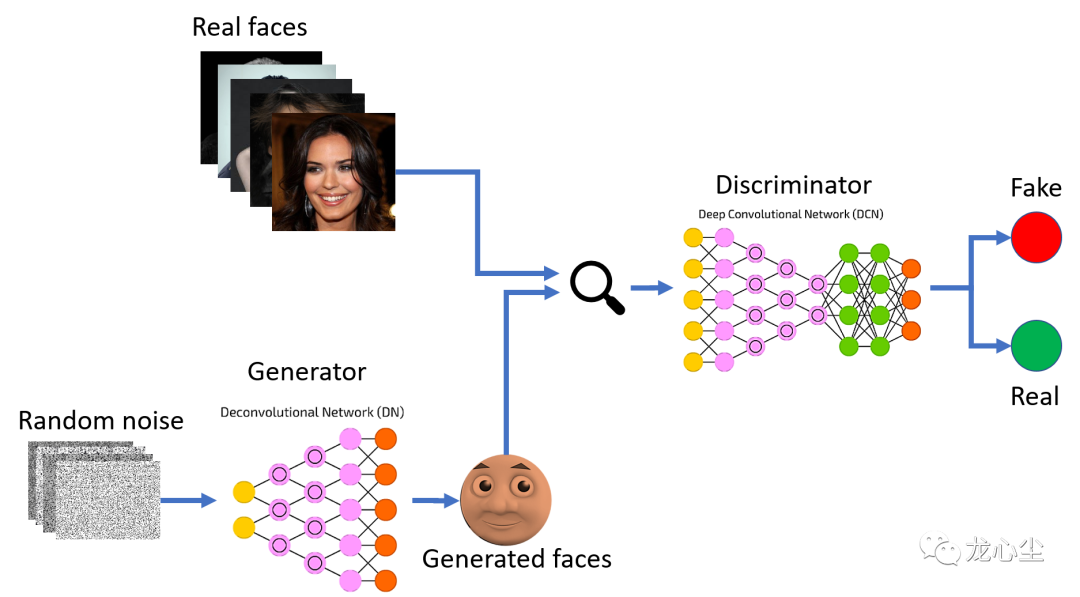
多智能体强化学习则是多个智能体的强化学习得到最优策略，并且各自的最优策略会影响对方智能体的下一步优化策略的过程。

或者理解成其认为博弈论收益函数是不确定的，需要对通过大量样本统计(长期收益的有监督学习)。典型的案例是AlphaGo、AlphaZero之类。

生成对抗网络(GANs)有点特殊，可以理解成有监督学习与无监督生成式算法的组合，前者（判别器）的优化目标是降低生成样本与真实样本的区分难度，后者（生成器）的优化目标是提升他们的区分难度。

而这两个目标是相互对立的，这又借鉴了博弈论的思路。这类算法在图像生成、图像修复、风格迁移等场景有非常多的应用。

另外，模型压缩算法可以理解成机器学算法与优化计算复杂度算法组合，在一定的误差容忍范围下显著降低模型的空间复杂度和推断时间复杂度。其典型应用场景是模型的实时运算加速、边缘部署压缩等。

04 小结一下

这里主要从面向优化的角度上串讲了以下12种思维方式不同的算法：加密算法、计算复杂度优化算法、最优化算法、有监督学习、无监督学习（降维、聚类、生成）、强化学习、博弈论、多智能体强化学习、生成对抗网络、模型压缩算法等。

因为是科普向，很多细节没展开，特别是机器学习算法和优化计算复杂度算法的各个流派没有探讨。

我们将在接下来的文章中进行更加详细的介绍。

点「在看」的人都变好看了哦！