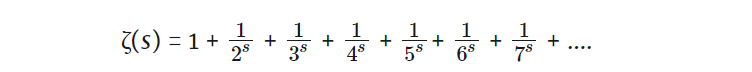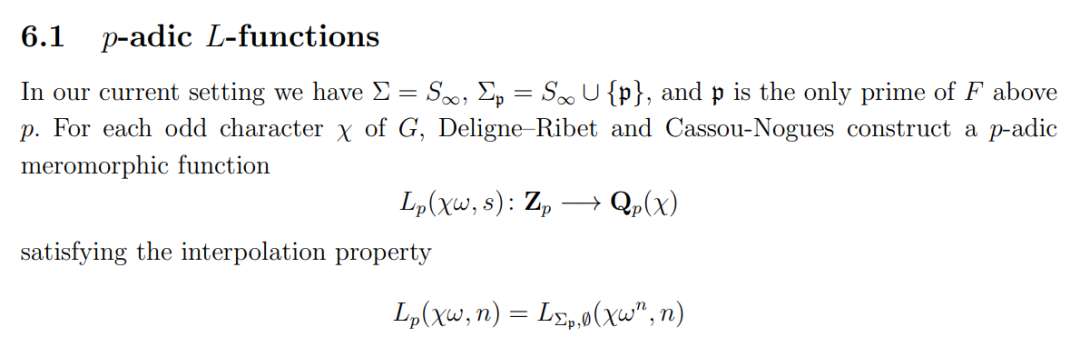本文约4300字,建议阅读10分钟
在解决希尔伯特第12个问题的过程中,计算机程序发挥了重要作用。
[ 摘要 ] 德国数学家大卫 · 希尔伯特提出的 23 个问题对二十世纪现代数学的发展起了非常积极的推动作用。这 23 个问题涉及了基础数学、数论、代数和几何以及数学分析等多方面,其中的大多数已经得到圆满或部分解决。其中未解决的第 12 个问题「一般代数数域的阿贝尔扩张」终于在百年之后得到了解决,还是以一种意想不到的方式解决。
德国数学家大卫 · 希尔伯特(David Hilbert)是二十世纪最伟大的数学家之一,被后人称为「数学世界的亚历山大」。他对数学领域做出了广泛和重大的贡献,研究领域涉及代数不变式、代数数域、几何基础、变分法、积分方程、无穷维空间以及物理学和数学基础等。1899 年出版的《几何基础》成为近代公理化方法的代表作,且由此推动形成了「数学公理化学派」。1900 年 8 月 8 日,在法国巴黎举办的第二届国际数学家大会上,大卫 · 希尔伯特提出了新世纪数学家应当努力解决的 23 个问题。这 23 个问题统称为「希尔伯特问题」,共分属四大块:1 至 6 属于基础数学问题,7 至 12 属于数论问题,13 至 18 属于代数和几何问题,19 至 23 属于数学分析问题。这些问题成为了后世数学家们努力攻克的难关,并对现代数学的研究和发展产生了积极和深刻的影响。一个多世纪过去了,这些问题中的大多数得到了圆满解决或部分解决,但有些依然未能解决,其中包括第十二个问题「一般代数数域的阿贝尔扩张(Abelian extension)」。就其定义而言,阿贝尔扩张是一类重要的域扩张,设 K 是域 F 的伽罗瓦扩域,若其伽罗瓦群 G(K/F) 为一阿贝尔群,则称此扩张为阿贝尔扩张,此时,K 称为 F 上阿贝尔扩域。1912 年,德国数学家埃里希 · 赫克使用希尔伯特模形式研究了实二次域的情形,虚二次域的情形用复乘理论已基本解决。一般情况下的阿贝尔扩张则尚未解决。其实,在希尔伯特提出他的 23 个问题清单前不久,数学家们就发现了一些与有理数相关的特定数字的构建块,其中这些有理数可以使用整数比例来表示。巧合的是,这一发现是解决第 12 个问题的基础,要求寻找与有理数以外的数字系统相关的构建块。经过数学家们数十年不断的研究探索,今年 3 月初发表在 arXiv 上的论文《Brumer–Stark Units and Hilbert’s 12th Problem 》终于描述出了希尔伯特 100 多年前寻找的用于广泛数字系统的构建块,但是得出的答案依赖一些非常现代的观点。论文地址:https://arxiv.org/pdf/2103.02516.pdf论文作者分别是杜克大学数学系教授 Samit Dasgupta(左)和印度科学研究院数学系教授 Mahesh Kakde(右)对于这项研究,美国数学家、加州大学圣地亚哥分校和哈佛大学名誉教授 Benedict Gross 表示:「这是我们期待已久的事情,他们确实取得了一项重大突破。虽然与希尔伯特的想法完全不同,但这就是数学的魅力。你永远无法预测以何种方式解决问题。」在解读这两位数学家的研究成果和方法前,我们首先来了解下希尔伯特第 12 个问题的数论基础以及百年来数学家们在此问题上做出的种种努力和尝试。希尔伯特第 12 个问题是建立在数论基础上,是研究数字的基本算术性质,包括多项式表达式的解,比如 x^3 + 2x − 3。特别地,数学家经常研究这些表达式的根,使多项式等于零的 x 的值。数论家经常根据多项式的系数类型来分类多项式。以有理数为系数的系数相对简单,是研究的共同目标。「我们从有理数开始,」杜克大学的数学家 Samit Dasgupta 说,他是这项最新研究的作者之一,还有一位合作者是来自印度科学研究院数学系教授 Mahesh Kakde。并表示道:「这是数论的基本系统。」有时有理系数多项式的根本身就是有理数,但情况并非总是如此。这意味着数学家想要找到所有有理数多项式的根,需要在一个展开的数系统中寻找:复数,包括所有有理数和实数,加上虚数 i。当在复平面上绘制多项式的根时,实数沿着 x 轴,纯虚数沿着 y 轴,某些对称性就会出现。这些对称性可以用来重新排列这些点,排列它们的位置。如果你能以任何顺序应用对称性得到相同的结果,那么多项式是阿贝尔式的。但是如果你应用对称性的顺序改变了结果,那么这个多项式是非阿贝尔式的。数论家对阿贝尔多项式最感兴趣,同样是因为它们的简单性,但它们很难区分。例如,x^2− 2 是阿贝尔式的, x^3 − 2 则不是。来自俄勒冈大学的 Ellen Eischen 说:「要想得到非阿贝尔式,你不必走得很远。」除了这些对称性之外,阿贝尔多项式还有一个显著的特点,那就是试图用简单而准确的术语来描述多项式的根。例如,很容易准确地描述多项式 x^2−3 的根:多项式的根是正负根 3。但是对于指数较大的复杂多项式来说,要写出它的根是很困难的。当然,也有变通的办法,「你可以用数字来近似『多项式的根』,」Eischen 说。但如果你想用一种明确的方式写下来,只能用有限的方式来写。然而,具有有理系数的阿贝尔多项式是特殊的:总是可以从固定的构建块集合中精确地计算它们的根。这个发现被证明是如此的强大,它启发了希尔伯特提出了他的第 12 个问题,而这一切都归功于一组被称为单位根的数字。单位根是一个看似简单却非常重要的概念。数值上,它们是多项式的解,其中,变量的幂被设为 1。比如, x^5 = 1 或者 x^8 = 1。这些解是复数,它们由指数中的数字表示。例如,5 次单位根就是 x^5 = 1 的五个解。但是单位根也可以用几何来描述,而不用方程。如果把它们画在复平面上,这些点都在一个半径为 1 的圆上。如果你把圆看作一个时钟,那么在 3 点钟指向,你总会有一个单位根,其中 x=1,因为 1 对任何幂仍然是 1。剩下的单位根在圆的周围等间距分布。19 世纪,在希尔伯特提出数学问题清单之前,数学家们发现,单位根可以作为他们想要研究的特定数字集合的「构建块」:具有有理系数的阿贝尔多项式的根。如果你把单位根简单地组合(用有理数加、减、乘)起来,你就能描述出所有这些期望的根。例如,5 的平方根是阿贝尔多项式 x^2-5 的根,并且可以表示为不同五次单位根的和。这与素数构建整数块的方式类似。因此,单位根需要精确的构造块,你需要用有理系数完美地描述阿贝尔多项式的根。另一方面,任何单位根的组合都会产生一个数,这个数是某个有理系数阿贝尔多项式的根。这两者有着千丝万缕的联系。希尔伯特在提出他的第 12 个问题时,想要让数学家们找到阿贝尔多项式根的构造块,它的系数来自有理数以外的数系统。换言之,对于其他数系统单位根有什么相似之处?这是一个雄心勃勃的问题,这也是它出现在希尔伯特清单上的原因。他猜想这个问题是可以回答的,因为他在提出这个问题时,就对另一种数字系统(称为虚二次域)组成构建块的描述方式有一个构想——大体上,该系统仅包含有理数和负数的平方根。几十年后,他的猜测被证明是正确的。伦敦帝国理工学院的 Alice Pozzi 说:「该问题有两种情况:『有理』情况和虚二次域情况。」希尔伯特希望以与这两种已知情况相似的方式描述其他数字系统的基本组成。这意味着要使用复分析(一种研究复函数的数学理论)。但是在 20 世纪 70 年代,希尔伯特的第 12 个问题已经提出几十年之后,数学家 Harold Stark 猜想可以借助 L 函数破解这个问题。L 函数是一类重要的复变数函数,通常以无穷级数表示,它是黎曼ζ函数的推广,黎曼ζ函数如下:
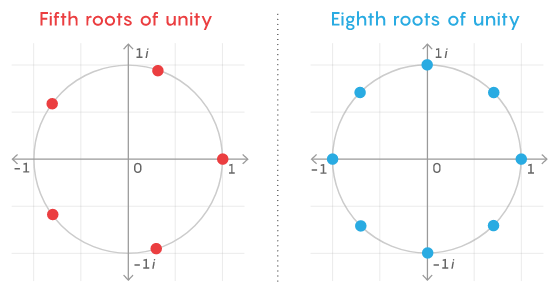
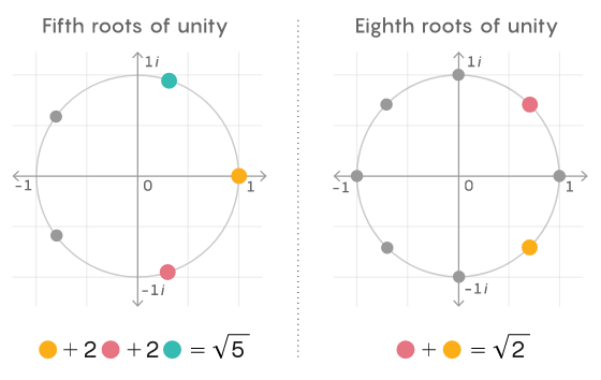
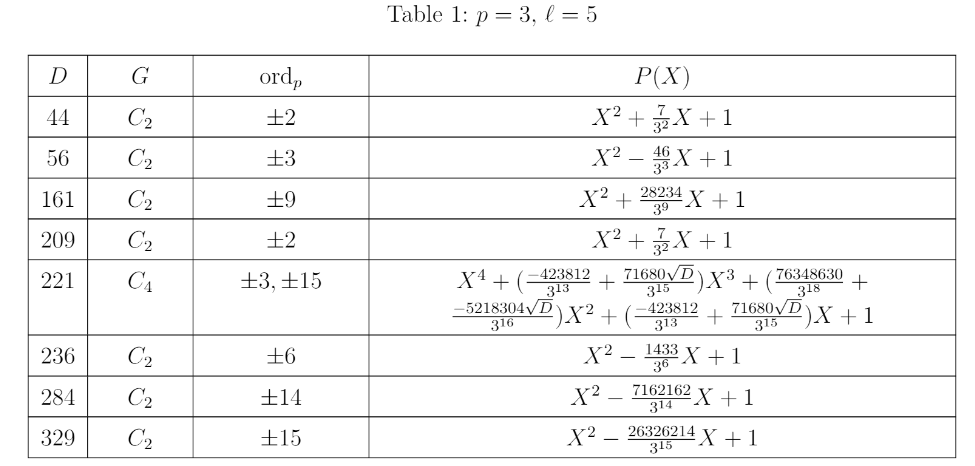
几个世纪以来,数学家都知道 L 函数是神秘并且极有意义的,它们给出了π等重要常数的无穷级数表示法。在这种直觉的基础上,Stark 能够使用 L 函数来模拟其他数字系统的单位根。然而,尽管数学家认为 Stark 的猜想是正确的,并且已经使用计算机分析法对其进行了广泛的测试,但他们并没有获得任何成功的证明。Darmon 说:「据我们所知,要证明 Stark 的猜想真的很困难,五十年来几乎没有任何进展。」因此,Stark 的猜想只是提供了一个简单的思路,他猜想可以使用 L 函数从其他数字系统找出含系数阿贝尔多项式的根的构建块,但是没人知道如何证明这一点。更糟糕的是,Stark 的方案只提供了实际描述组成构件块所需要的一半信息。就像要在地图上寻找一个位置,只提供了经度,还需要纬度才能找到特定的地点。20 世纪 80 年代,Benedict Gross 发表了 Stark 方案的修改版本来继续这项数学研究。希尔伯特和 Stark 都曾考虑使用复数,而 Gross 使用了 p 进数(p-adic numbers)。这两种方法都是标准数字的替代方案,标准数字使用不同的方法来确定两个数字是否接近。利用 p 进数可以重写数学中的许多概念,其中包括 L 函数。实际上在现代数论中,p - 进 L 函数与复 L 函数的关系非常密切。即便如此,起初 Gross 将复数转换为 p 进数似乎却没有让 Stark 猜想的证明问题更进一步。在随后的几十年中,随着数字理论领域 p 进数数论的发展,Gross 的 p 进数猜想变得容易了一些。Darmon 说:「借助 p 进数分析能够得到许多有趣的结果。」事实证明,相比于复数,使用 p 进数更容易解决数学中一些重要的问题,希尔伯特的第 12 个问题恰恰如此。今年 3 月,杜克大学教授 Samit Dasgupta 和印度科学研究院教授 Mahesh Kakde 发表的这篇论文首次使用 p - 进数 L 函数回答了希尔伯特关于独立大型数字系统的问题。这些数字系统被称为「全实域(totally real field)」,是有理数的延伸,并包含给定多项式的一个根。p - 进数 L 函数。两位教授通过 Deligne–Ribet 和 Cassou-Nogues 构造了一个 p 进数亚纯函数,并满足插值性。2004 年,Dasgupta 在其博士论文中首次提出了所需要的最终公式——对 Gross 的猜想进行了改进。此后的十年里,利用 p 进数数字理论的发展,他又先后发表两篇论文并最终证明了 Gross 的猜想。但这还不足以解决希尔伯特的第 12 个问题,因为与 Stark 猜想一样,Gross 的猜想只提供了精确描述构建块所需的两个数字之一。在过去的三年里,Dasgupta 和 Kakde 合作想要证明能够提供构建块所需的两个数字的 Gross 猜想,尽管看起来可能无法实现。Kakde 曾说道:「我们两人都非常乐观。有时会遇到难以解决的障碍,但幸运的是,我们一直在取得进展。」直到 2020 年,他们终于有了突破,证明了与全实域相关的精确构建块的确存在。换言之,他们知道自己想要实现的东西就在某个地方,并指引他们朝着正确的方向前进。他们得到了用以证明完整描述构建块的精确公式存在的关键方程式。为了验证正确性,Dasgupta 的两名学生编写了一个计算机程序,由此生成了用于给定数字系统的构建块,并展示了工作原理。除了理论证明之外,这个计算机程序还帮助证明了 Dasgupta 和 Kakde 提出的公式的正确性,这是解决此类抽象问题的一个重要因素。此外,这个计算机程序在 GitHub 上有一个项目,名为「Computation-of-Elliptic-Units」,主要计算「生成实二次域希尔伯特类域所需的椭圆形单位和多项式」。下表 1 为一部分计算结果:项目地址:https://github.com/liuyj8526/Computation-of-Elliptic-Units希尔伯特的第 12 个问题要求精确描述阿贝尔多项式的根的构造块,类似于单位根,Dasgupta 和 Kakde 的研究给出了一系列数字系统的构造块,尽管是以 p - 进 L 函数的形式,具有明显的现代性。但还有最后一个问题:既然希尔伯特明确地写道,构建块应该由复数组成,那么这个解偏离希尔伯特最初的指令,这显示了数学的通用性。使用 p 进数分析为希尔伯特的问题提供了答案,但使用复分析的原始问题仍需未来的数学家探索。可能有很多方法来描述构建块,未来也许能够使用复数来描述它们,从而满足希尔伯特的最初要求。正如 Gross 所说:「这是一场接力赛,当你精疲力尽时把接力棒传给下一个人。」参考链接:https://www.quantamagazine.org/mathematicians-find-polynomial-building-blocks-hilbert-sought-20210525/






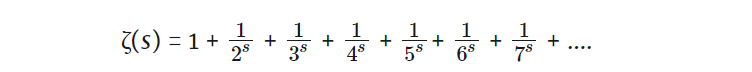

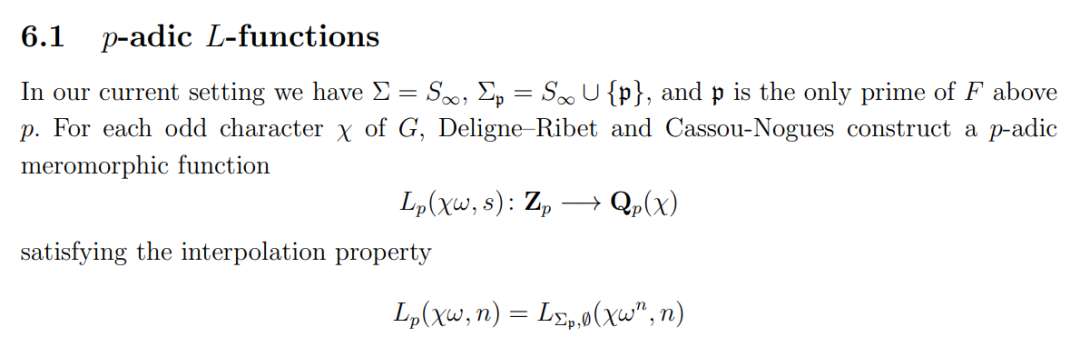

 下载APP
下载APP