骰子、量子力学与宇宙天体：一个随机数的诞生

全文4660字，阅读约需10分钟

文｜油醋

来源｜品玩

ID：pinwancool

题图｜Pixabay

滑落、滚动、不停微颤，直到恢复静止。

没有人不曾见过骰子落下那一刻的场景。

第一颗骰子在一座公元前24世纪的中东坟墓里被发现，这成为人类寻找随机数列的最早印记。

生于18世纪法国的著名天文学家拉普拉斯相信后者，他认为自然界和人类社会普遍存在客观规律和因果联系，宇宙中的任何事物或事件都是，并永远是自然规律的结果。换句话说，万事万物，有因必有果。

机械决定论笼罩了经典力学，直到量子力学理论出现，表明宇宙中的基本粒子在观测的一刻坍缩到概率波的一个确定位置上，这个“位置”的确定被认为是真正意义上的随机事件。

但是爱因斯坦仍然相信，现出纯碎随机性的量子力学只是另一种更高维度的确定性理论的一个局部。作为反驳，世人记住了一句“上帝不会掷骰子”。

故事又回到骰子。

事实上，哪怕把骰子从物理世界中抽象出来，变成一个质量均匀，形态趋近于完美球体的无限多面体，它也无法成为突破机械决定论的反例。但即便如此，这也并不妨碍很少有一个结构如此简单的物体会具备这样深邃的形而上学含义。

它本身是一个不完美的随机数生成器。

图源：Techspective

时至今日，从现代密码学、工业设计再到人工智能学科，对随机数的需要无处不在。随着经典计算机的发展与量子计算机的出现，更多的随机数生成器不断出现，然后又在更强大的算力下暴露出规律，失去效用。寻找更接近完美的随机数发生器这件事，与前沿科技的突破一直并行向前。

澳洲国家天文台的科研团队近日在ELSEVIER上公布了一项最新研究。一种全新的随机数捕获方法出现并通过了NSP800标准，这个随机数生成器的位置距离地球510光年，是一颗脉冲星。

脉冲星，会成为那个完美的骰子吗？

脉冲星制造随机数

脉冲星是一种高速旋转的中子星，因不断地发出电磁脉冲信号而得名。因为极快的自转速度（毫秒脉冲星转速可达每秒1000转）以及极高的天体密度（可达10亿吨每立方厘米级别），使其具备地球上的实验室所无法复现的极端物理性质。

最为人熟知的特性之一是，脉冲星的自转具有非常稳定的周期性，是自然界最精准的天文时钟。虽然其消耗自转能弥补向外辐射能量的过程会导致自转逐渐放慢，但是这种变慢速度非常微小，周期稳定度可以达到达到10的负19次方——换句话说，一颗脉冲星的自转周期相隔3170亿年左右会出现1秒的变化，这比目前最稳定的氢原子钟还要高1万倍以上。

图源：space.com

除此之外，脉冲星辐射的许多特性表现出明显的随机性，这些随机特征可以被分为两类，第一类需要在一个较长的时间尺度上观察，比如一年后脉冲星自转周期的不规则变化；另一类则可以被直接观察到的，比如每一次脉冲辐射的亮度变化或两次脉冲辐射之间脉冲形状或相位的变化。

每一次脉冲的通量密度——即单位时间、单位面积，单位频率或单位波长所接收到的辐射能——是可以直接单次观察到的脉冲星特性之一。

此前的研究证明，绝大多数脉冲星的通量密度分布遵循对数正态分布或幂律分布，但当前并不存在可以准确预测单次脉冲通量密度的物理学理论。也就是说，根据脉冲通量密度所形成数列的随机性，具有很好的随机性潜力。

澳洲国家天文台的科研团队利用了这一点，将脉冲星的脉冲通量密度作为一个全新的随机数生成器。

这次试验选定了510光年之外，自转周期0.00575秒的脉冲星PSR J0437-4715作为观测主体。

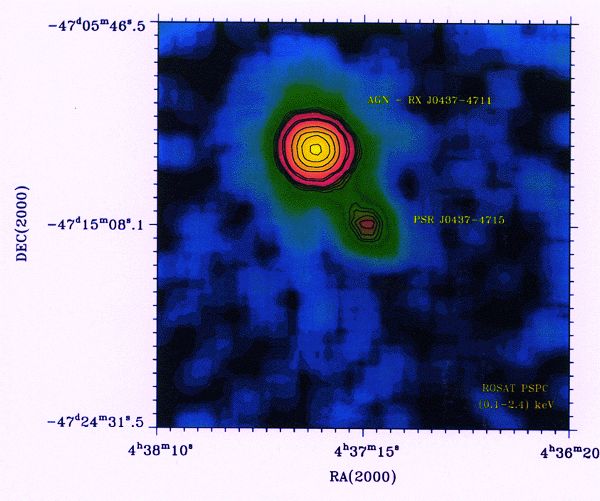
脉冲星PSR J0437-4715。图源：HEASARC

对于这颗脉冲星在一个时间段内通量密度的获取，由位于澳大利亚新南威尔士州的帕克斯射电天文台独立完成。团队在论文中透露了与观测相关的具体细节，数据获取的时间在2020年3月30日凌晨，团队使用了256MHz频带上的512个频道进行记录，中心观测频率达到1369 MHz。

获取到的随机序列通过三种不同的数据处理方式处理，再放入一个随机数列测试中验证是否达到真正的随机数标准。当一个数列越长，其随机性被验证的可信度也越高，这次观测的总时长达到两个小时，相当于收集了这颗脉冲星连续发出的120万次脉冲信号。

团队选择了SP800-22作为随机数的测试标准。这套由美国国家标准技术学会（NIST）公布的标准是目前世界上对于随机数列接受度最高的判断标准之一。通过同时计算多个比特数据来考察被检测序列是否满足随机序列在周期性、相关性和分布特性等方面的特征，以判断此序列是否随机。

最终的数据表现十分理想，脉冲星通量密度所形成的随机数列顺利通过了SP800-22的测试标准。

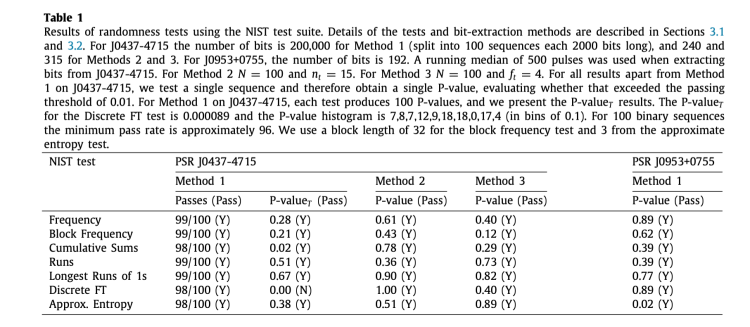
观测生成的随机数列顺利通过了SP800-22标。图源：论文《Physical publicly verifiable randomness from pulsars》

借助宇宙天体来获取随机数，这是通过物理现象获得随机数的方式之一，与骰子、扑克一样，脉冲星或可以被称为一个物理性随机数生成器。研究团队在论文开篇就强调了这一点。而在脉冲星与随机数产生关联的背面则是另一场担忧。

随机性通常被认为是安全、隐私、信任以及公平的基础。一旦随机数的生成机制被攻破，任何加密方法也会显得不堪一击。

几年前，美国爱荷华州彩票公司被曝出一位负责曾负责设计和维护计算机摇奖机的安全部门主管在近十年间依靠篡改摇奖机程序，购买彩票非法领取奖金超过200美金。这其中的“计算机摇奖机”，就是一个用于生成彩票号码的随机数生成器。

纪录片《The Importance of Being E.R.N.I.E.》片段

在这种局面下，PVR协议（可公开验证的随机性）作为当下面临多方环境的解决方法出现，当前最先进的 PVR 系统往往建立在被认为普通算力难以解决的数学问题之上，比如分解大整数或者寻找离散对数。但随着超级计算机的算力在近几十年的飞跃式增长，随机数生成器的规律被找到已经从天方夜谭变成隐忧。在超级计算机之后，在算力上对前者来说无异于降维打击的量子计算机正在入场。

“只要是基于数论，一切对于量子计算机来说就不成问题。”

随机数的真伪之争

基于真实的物理世界，或者基于计算机与数学模型，两者将随机数划分出“真伪”。

伪随机数指的是生成于计算机内部的随机数，比如下面这个谷歌所提供的伪随机数生成器。

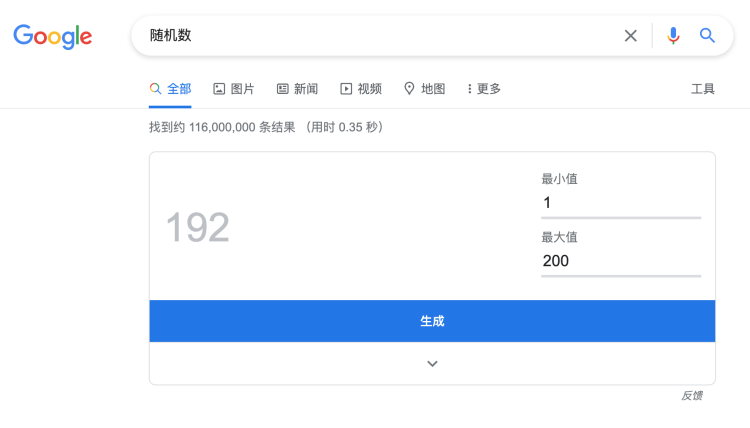图源：Google

在这个体系内，来自计算机主板上的定时或计数器在内存中的记数值被选定为“种子”，作为让这个运算开始并产生随机数列的第一块多米诺骨牌。但这里的问题在于，生成随机数列的递推公式是可预见的，这意味着当输入的随机数种子相同，其所输出的随机数列会对应一致，这种随机伴随着一种紧密的映射关系。

真随机数则指的是物理世界中出现的随机数。与伪随机数生成器相比，真随机数生成器需要满足一层凌驾于算法实现的要求——不可复现。即当生成器接收到两次相同的输入操作，也仍然会生成两组不相同的随机序列。

骰子是我们最容易理解的真随机数发生器之一。如果粗糙的将“投掷骰子”作为一个相同的输入值，连续投掷十次为一个随机序列，一个人投掷三组（大概率）会得到三组不同的随机序列，这既是不可复现。

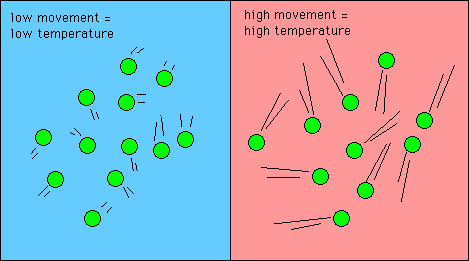
物理世界中，利用原子的热运动是寻找真随机数的可靠方法之一。

图源：Google

温度高于绝对零度的原子都存在热运动，这些热运动的副产品之一，是其会在电路中产生噪声。噪声会引发电路中的电压产生微弱波动，CPU里内置的真随机数生成器就是通过放大这些电路中的热噪音来产生随机数。

相比完全基于算法的伪随机数生成器，真随机数生成器所处的物理环境更加复杂，涉及的变量更多，这导致其具有更优越的随机性。但即使如此，在经典力学的范围内，只要所有变量的初始状态确定，这个系统其实依然在按照一种确定性的原理运行，由此而得出的随机序列自然也是可以预测的。

换句话说，基于热噪声的随机数发生器被从“伪”随机数中区分出来，很大程度上是因为这个综合的“输入值”太难测量了，这仍然不是最理想的随机序列。以最严苛的假设环境来看，最理想的真随机数生成器只能在经典物理之外具有内禀随机性的量子力学中去找。

另一层意义：跨越PVR

从这个角度上来看，当人类能够完全掌握脉冲星的天体特性，后者理论上也不会是完美的真随机数发生器，而这又不免走向了拉普拉斯的决定论——如果在这一刻，你知道宇宙中所有基本粒子的位置和速度，你就知道了宇宙的所有的将发生的事情。

拉普拉斯

因此，研究团队对于用脉冲星来捕获随机数满足了通过了NSP800之外，有另一层更现实的考虑。研究团队试图利用遥远的脉冲星来完全跨越PVR的协议标准，脉冲星或许是最简单直白的可公开验证的随机数生成器。

随机数产生中的“可公开验证的随机性”可以被分为五方面的要求：

可得性：没有任何一方可以封锁信号源，并且任何人都可以在任何时间使用这个信号源。

不可预测性：没有任何一方可以预测未来的随机序列。

不可变性：没有任何一方可以影响未来的随机序列。

可公开验证性：任何一方都可以核对已经生成的随机序列的正确性。

无第三方：不需要另外的可信服务器来启动或管理随机数生成器。

之前已经提及，脉冲星单次脉冲通量密度无法预测，并且地球上的研究者都无法对几百亿光年外的脉冲星产生影响或者遮蔽脉冲信号。于是最重要的一点就落在其中的“可公开验证性”上。

研究团队在测试试验中设置了另一颗脉冲星PSR J0953+ 0755，这颗脉冲星就是为了验证“可公开验证性”，即同一个随机数生成器上生成的同一段随机数列，是否可以由两台观测设备在不同方位得出。与帕克斯天文台形成参照的另一台射电望远镜，则是8000公里外，位于中国贵州的天眼FAST。

从实验结果来看，同一时刻的两台射电望远镜指向了相近的观测结果。

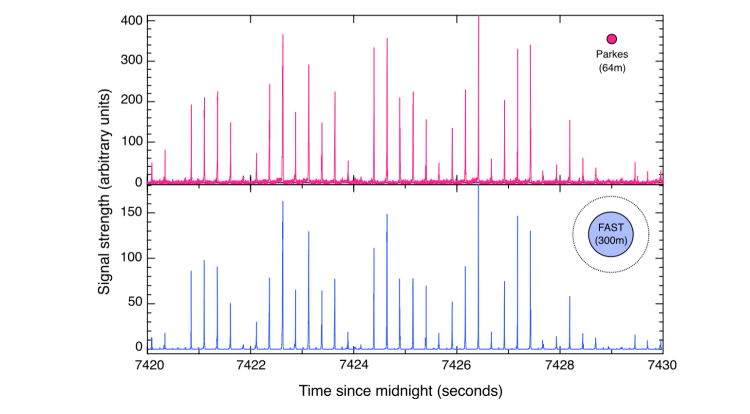
帕克斯天文台（上）与“中国天眼”FAST对于脉冲星PSR J0953+ 0755的脉冲信号观测结果。图源：论文《Physical publicly verifiable randomness from pulsars》

从1964年冯·诺依曼发明了平方取中法开始，人类在寻找随机序列时先选定一个随机数种子，再经过复杂算法生成数列的逻辑就没有变过。到了1997年，来自硅谷的一个团队发明了LavaRand——一款硬件随机数生成器，与之前依靠计算机的逻辑不同，LavaRand用一个网络摄像头来对着熔岩灯拍照。从摄像头中过来的图片数据是一个真实的熵源，可以以165kb/s的速率生成随机数，随机数生成器开始接入真实的物理世界。

统计学家 Francis Galton在1890年的《Nature》杂志中表达了对骰子的钟爱，“在所有的产生随机数的事物中，没有什么能够比骰子更加优越了”。

统计学家 Francis Galton在1890年的《Nature》上的文章

“当它们在容器中不断地摇晃，互相碰撞，与容器壁剧烈的相抵，它们在容器中的样子是完全不可预见的，此时再摇晃一下，一切又重新打乱。”

130年之后，对宇宙的探索不断带来新的启发，人类第一次将寻找完美骰子的目光聚焦到脉冲星上。此次的研究表明，即使通过研究单一的可观测特性，已经可以为随机序列的研究提供了很多选择。未来研究团队可能会尝试改变观测的目标特性，将到达时间抖动（arrival time jitter）、噪音等其他脉冲星的特性也纳入测试。

这个无垠的骰盅里，透进的光亮还太少，因此每一次主动发起的探索都格外迷人。

*参考资料：Physical publicly verifiable randomness from pulsars

本文由品玩授权亿欧发布，申请文章授权请联系原出处。