从头开始编写一个时间序列数据库

作者 | Ryo Nakao

译者 | 王雪迎   责编 | 张红月

出品 | CSDN（ID：CSDNnews）

本文翻译自Ryo Nakao 的个人博客（https://corecursive.com/066-sqlite-with-richard-hipp/）主要告诉大家如何实现一个时间序列数据库引擎。它是作者的经验之谈，是我在从头开始编写一个轻量级时间序列数据库引擎中所学到的。

虽然本引擎用Go语言编写，但文中所涉及的绝大部分内容与编程语言无关。

动机

我一直在研究一些处理海量时间序列数据的工具。其中之一名为Ali（https://github.com/nakabonne/ali），是一个负载测试工具，可以在客户端实时绘制度量值。它请求执行特定的查询，并将每个查询的结果，如延迟或任何其它度量，进行无休止地写入。换句话说，这有点像在一台主机上创建一个带有简单查询功能的推送监视系统。

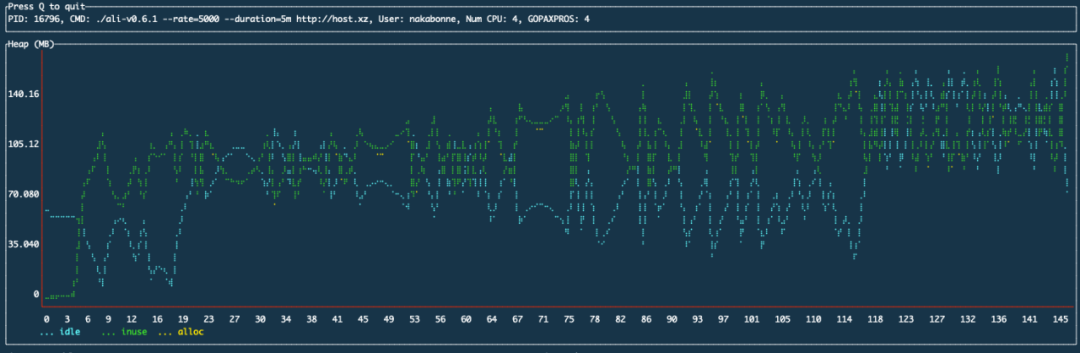
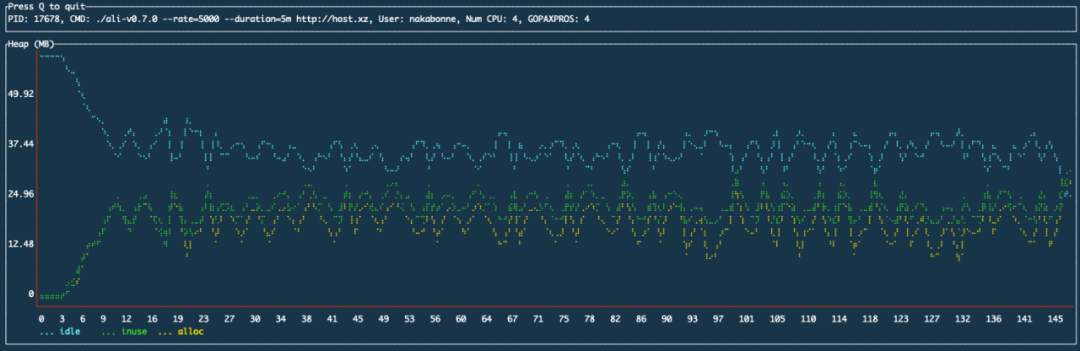
在以前的实现中，它只是将数据点追加到堆上的变长数组中。这种做法自然会导致一个问题，即随着时间的推移，内存使用量将不断增加：

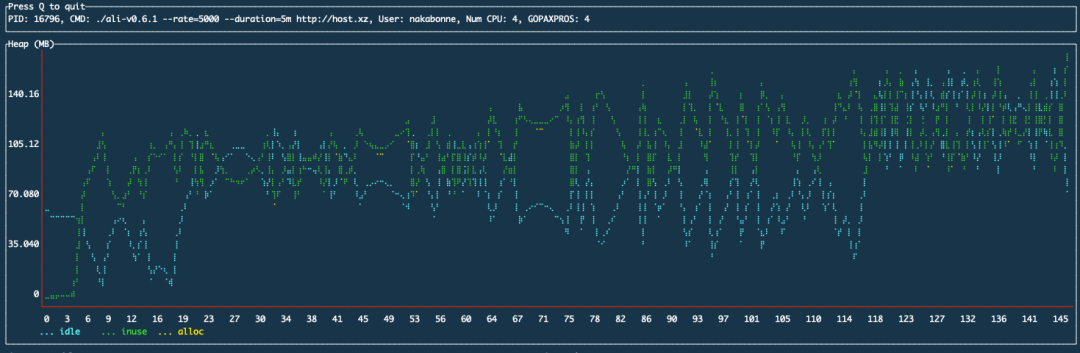
由nakabonne/gosivy测量的Ali堆使用量

为了解决这个问题，我尝试开发了一个存储引擎，可以被用作Go程序库。

时间序列数据的特征

我们首先要了解时间序列数据，以便理清需要解决的问题。

时间序列数据是具有时间戳的多个值的集合。它一般被用于观察随时间变化的数据。每个时间序列数据都被称为数据点，通常表示为一个带有时间戳和值的元组。时间序列数据具有以下特征：

1.数据量巨大

由于时间序列数据的性质，单个数据点很少有意义，只有在收集了大量数据之后，它才会变得有效。在金融行业里，数据捕获要求超过1000000/s次的情况并不少见，因为数据通常是在短时间内写入的。

在Ali的用例中，用户指定的请求速率与写性能需求直接相关（尽管文件描述符数量的上限基本上是瓶颈）。

为了处理海量数据，我们需要集中精力尽量优化数据写入过程，还需要尽可能减少磁盘空间的消耗。

2.只追加

每个数据点都是不变的。而且，通常会对较老的数据执行批量删除操作，而不指定特定数据点。

3.按时间排序

由于数据按时间戳排序存储，因此可以将其视为已按时间索引。利用这一性质你可以在没有任何开销的情况下建立索引。

4.批量访问

在读出数据时，主要是通过指定一个时间段来检索具有连续时间戳的多个数据点。你可以利用此特性来提升数据读取时的局部性。

5.最近优先

在许多用例中，我们倾向于读取和使用最近的数据点。这可能会影响缓存算法的选择。

6.高基数

时间序列数据往往具有更高的基数。例如，在系统监控环境中尤其如此。云原生时代，我们得到了更多的机会来监控动态变化的主机和网络等环境。

从这个意义上说，几乎没有完全相同的度量标准；为每个度量创建一个文件将导致各种问题，例如inode限制。

现有解决方案

总体来说，我们发现对时间序列数据的操作是写密集型，并且很多情况下是在一个时间范围内顺序读/写数据。

Google的LevelDB是一个众所周知的键-值存储引擎，并已发布了一些Go语言的实现。LevelDB是基于LSM树实现的，它只对尾部进行顺序写入，适用于只追加的时间序列数据。按键排序也使它适合于基于时间戳的时间序列数据。事实上，早期的Prometheus和InfluxDB存储引擎也是基于LevelDB的。

然而有一些东西被浪费了。我们将在后面看到，时间序列数据是单向的，可以利用此特性将其编码成更小的尺寸。我们希望利用这一点，因为要处理的是海量的时间序列数据。

另外，由于所有数据点都是不可变的，无需更新过程，因此所有写操作都可以按顺序进行。尽管如此，我还是有点担心，在执行诸如合并SSTables等操作时会发生写放大。

tstorage

有鉴于此，我决定自己编写一个数据库引擎库，命名为tstorage。

它是一个使用本地磁盘的轻量级引擎，完全用纯Go语言编写。

本文介绍了我是如何实现tstorage的，并解释了创建它所需的知识。

什么是数据库引擎

典型的DBMS处理来自客户端的请求，并控制节点之间的通信以进行集群。它还解析查询，制定执行计划，并根据这些计划从磁盘读/写数据。数据库引擎是只执行最后读/写部分的组件，也是下图中存储引擎的一部分。

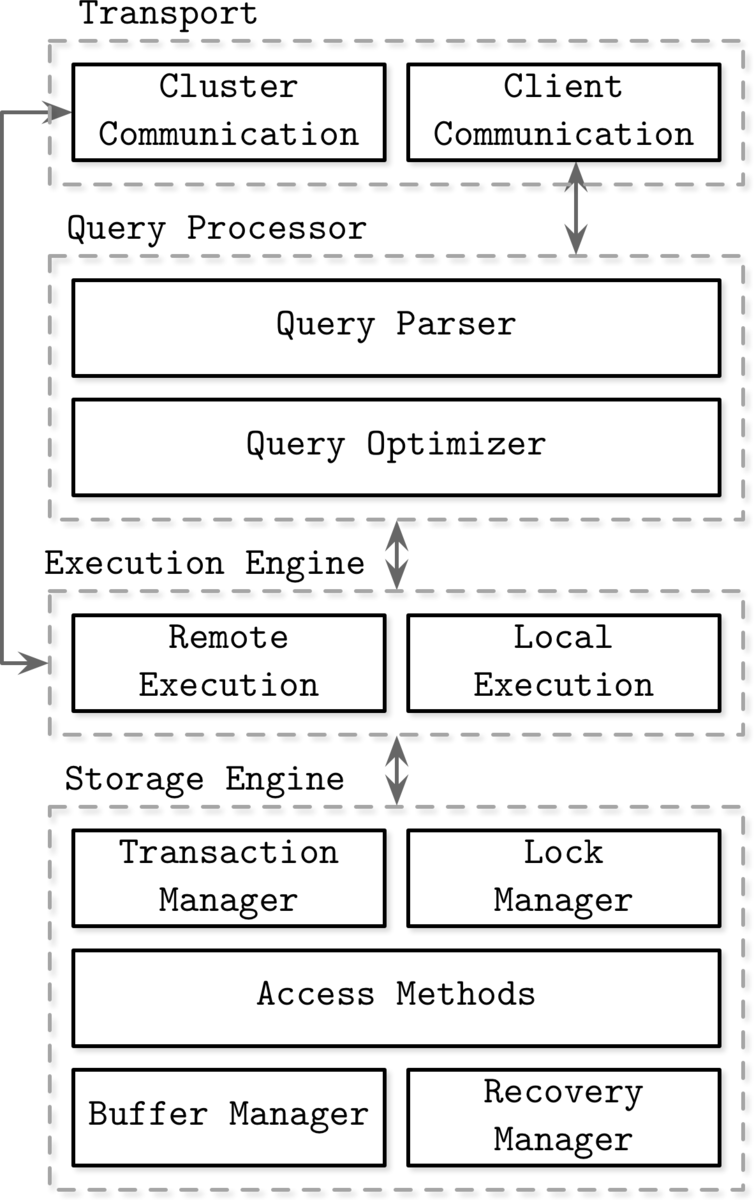
数据库内部结构，Alex Petrov，2019，第1章，图1-1。数据库管理系统架构

数据库引擎对磁盘/内存上的数据结构进行抽象，为图中所示的执行引擎提供API，并提供了事务和恢复功能。

数据模型

基于这些特性，tstorage采用了一种按时间划分数据点的线性数据模型结构。每个分区充当一个完全独立的数据库，包含其时间范围内的所有数据点。

  │                 │Read              Write  │                 │  │                 V  │      ┌───────────────────┐ max: 1600010800  ├─────>   Memory Partition  │      └───────────────────┘ min: 1600007201  │  │      ┌───────────────────┐ max: 1600007200  ├─────>   Memory Partition  │      └───────────────────┘ min: 1600003601  │  │      ┌───────────────────┐ max: 1600003600  └─────>   Disk Partition         └───────────────────┘ min: 1600000000

受LSM树的轻微影响，Prometheus的V3存储也使用了一种非常近似的模型

只有头和下一个分区在堆上并且是可写的。这称为内存分区。在内存分区中，数据在写入之前会先被追加到预写日志的末尾，以防止数据丢失（如果不需要这样的持久性，可以将其关闭）。

旧分区会写入磁盘上的单个文件。这称为磁盘分区，是只读的。写入磁盘的文件通过mmap（2）内核透明地缓存，后面将解释这点。

你可以为分区设置一个时间段，在这段时间之后，新的内存分区将被自动添加到堆头，旧的内存分区将被刷新到磁盘。

这种模式有许多优点。首先，读取时可以完全忽略指定范围之外的分区。这种尽可能缩小搜索范围的想法，是受到了LevelDB中使用的布隆过滤器的启发。另外，因为最新的数据点缓存在堆中，所以大多数都能被快速读取。

除此之外，由于tstorage被设计成将一个分区写入一个文件：

所有的写操作都只能追加，而不会发生任何写放大，因为它只按顺序写入一个文件。

文件的数量不依赖于基数（度量类型的数量）。

如前所述，读取操作通常指定一个时间段并获取相邻的数据点，因此提升了局部性。

以下部分描述每种分区实现中的关键点。

内存分区

1.数据点列表

数据点列表被表示为堆上的一个数组（从技术上讲，它有点像Go语言中指向名为Slice的基数组的指针列表）。这是一个包含无限多个要写入的数据点的列表，因此乍一看，链表似乎是最佳选择，因为它能使用O（1）复杂度添加元素。然而，内存中元素相邻排列的数组将受益于高速缓存的空间局部性。此外，由于时间序列数据总是预先排序的，因此可以很容易地实现二分搜索等经典搜索算法。

2.无序数据点

在实际应用中，由于网络延迟或时钟同步等问题，数据点出现无序的情况并不少见。写入时应考虑到这一点，分区中的数据点应始终保持有序。

但是要注意，在将数据点作为数组进行管理时，每次写入都需要应用一个独占锁。我们必须考虑一种很酷的方法来接收它们，这样就不必延长锁定时间来容纳无序的数据点。

无序数据点可以分为两种情况：一是它们在要写入的分区范围内无序；第二种情况是数据点超出了首先尝试写入的分区的范围。

如果写入的数据点对应于第一种情况，我们将先在一个单独的数组中无序地缓存数据点。然后，在刷新到磁盘时，数据点与内存分区中的数据点合并并重新排序。

在数据模型部分，我提到堆上只有头部及其下一个分区，以适应第二种情况：在头部添加新分区之后，可能会立即写入跨分区的数据点。这是为了解决第二种情况。通过使最近的两个分区保持可写状态，我们可以避免这些数据点被丢弃。

3.预写日志（WAL）

内存分区使用易失性存储，因此有可能由于突然崩溃或掉电而导致数据丢失。为了应对这个问题，内存分区首先将操作日志写入预写日志（WAL）。在发生崩溃的情况下，你可以通过执行从日志开头到结尾写入的操作进行恢复。

对于支持磁盘上数据更新操作的数据库引擎，WAL必须执行非常低级别的操作：要完全恢复更新所做的处理，必须准确地存储哪个磁盘块中的哪个字节被更改，等等。

但是，时间序列数据是只追加的，tstorage会将所有磁盘分区都置为只读。它只需要附加有关哪些数据点已被写入内存分区的高级信息，这样就可以用简单且与磁盘无关的格式来恢复它们。

磁盘分区

理解磁盘分区的最快方法是查看文件系统上的宏布局。

如下所示，每个分区使用一个目录，其下面是元数据和实际的压缩数据。这是普罗米修斯布局的简化版本，所以你以前可能见过类似的结构。

$ tree ./data./data├── p-1600000001-1600003600│   ├── data│   └── meta.json├── p-1600003601-1600007200│   ├── data│   └── meta.json└── p-1600007201-1600010800       ├── data       └── meta.json

我将按照数据->元数据的顺序来描述实现点。

1.内存映射数据

如上所述，分区中的所有数据点都被写入一个文件。tstorage采用以下格式。

 ┌────────────┐    │    度量-1    │度量-2  │    │────────────│    │ 度量-3 │              │    │────┘              │    │          度量-4        │    │────────────│    │   度量-5  │   度量-6  │    │────────────│    │         度量-7     │  │    │──────────┘  │    │         度量-8         │    │────────────│    │度量-9│     度量-10    │    └────────────┘             文件格式

度量-1～度量-10分别表示度量的数据点列表

回忆一下时间序列数据的特征。数据点是不可变的，而且大多数情况下，度量是通过指定一个范围来批量获取的。因此，我们可以通过按度量对数据点进行分组来提高局部性。

这个文件通过mmap（2）中的内核透明地缓存。这使得我们可以缓存文件而不将其复制到用户空间。这个方法非常有效，因为我最初的动机就是解决Ali随着时间的推移吃光堆的问题。

内存映射文件可以被Go程序以[]bytes形式访问，就像堆上的一个字节字符串一样。

type diskPartition struct {  // file descriptor of data file  f *os.File  // memory-mapped file backed by f  mappedFile []byte

现在，我们如何搜索这个自包含的字节序列呢？将它复制到堆上，并在Go程序中对其解码为数据结构是很容易的，但这达不到内存映射的目标。反正，我们需要一个索引结构来有效地访问编码数据。接下来介绍的元数据用于此目的。

2.元数据

元数据的内容如下所示。一个分区只有一个元数据，这就是为什么采用JSON格式，虽然有点多余，但很容易通过编程进行处理。

$ cat ./data/p-1600000001-1600003600/meta.json{  "minTimestamp": 1600000001,  "maxTimestamp": 1600003600,  "numDataPoints": 7200,  "metrics": {    "metric-1": {      "name": "metric-1",      "offset": 0,      "minTimestamp": 1600000001,      "maxTimestamp": 1600003600,      "numDataPoints": 3600    },    "metric-2": {      "name": "metric-2",      "offset": 36014,      "minTimestamp": 1600000001,      "maxTimestamp": 1600003600,      "numDataPoints": 3600    }  }}

元数据用于在分区中构建索引。这是存储每个度量的文件内偏移量和字节大小的地方，只有这些元数据才能进入堆。通过这些信息，tstorage尝试随机访问映射到内核空间的数据。类似于：

   {       "minTimestamp": 1600000001,       "maxTimestamp": 1600003600,       "numDataPoints": 7200,       "metrics": {         "metric-1": {           "name": "metric-1",   ┌─────  "offset": 0,   │       "minTimestamp": 1600000001,   │       "maxTimestamp": 1600003600,   │       "numDataPoints": 3600   │     },   │     "metric-2": {   │       "name": "metric-2",   │       "offset": 36014, ────────────┐   │       "minTimestamp": 1600000001,  │   │       "maxTimestamp": 1600003600,  │   │       "numDataPoints": 3600        │   │     }                              │   │   }                                │   │ }              ┌───────────────────┘   │                │   V                V   0              36014   ┌───────────────────────────┐   │    Metric-1    │ Metric-2 │   │───────────────────────────│   │ Metric-3 │                │   │──────────┘                │   │          Metric-4         │   │───────────────────────────│   │   Metric-5  │   Metric-6  │   │───────────────────────────│   │         Metric-7      │   │   │───────────────────────┘   │   │         Metric-8          │   │───────────────────────────│   │Metric-9│     Metric-10    │   └───────────────────────────┘

为了存储每个度量的起始偏移量，我们需要在刷新到磁盘时将其持久化。即对每个度量的数据点列表进行编码，并在构建索引时将偏移量写入元数据文件。

编码

如前所述，时间序列数据通常由时间戳和值的元组表示，这就可以将其巧妙地编码为非常小的尺寸。

2015年，Facebook发表了一篇名为Gorilla：一个快速、可伸缩的内存时间序列数据库的论文，他们在其中引入了一种利用时间序列数据特征的编码方式。当前许多主流的时间序列数据库都基于这种编码方式，而tstorage也是如此。

时间戳和值使用不同的方法进行编码。首先，tstorage中的UNIX时间戳表示为一个无符号的64位整数。由于该时间戳趋向于单调递增，仅存储与先前值差异的编码方法是有效的。因此，使用Delta-of-delta编码。

此外，tstorage中的值表示为有符号的64位浮点类型。该值使用XOR编码，因为它倾向于保持接近这个值，尽管它不可能单调地增加或减少。

我将解释每种编码方式。

1.Delta编码

Delta-of-Delta编码是一种利用Delta编码的方法，因此我将先解释一下Delta编码。

Delta编码只写入上一个数字和当前数字之间的差异。

例如，假设第一个时间戳是160000000。如果后面写入1600000060->160000120->160000181，则增量分别为60、60、61。

只将这些增量值按顺序写入文件。解码时，只需按顺序应用增量值，就可以恢复原始值。

2.Delta-of-delta编码

即使使用delta编码，一些可变长度的编码结果也可以足够小。然而，时间序列数据的时间戳通常具有固定的间隔，并且增量值本身很可能彼此接近。因此，利用这个增量值的增量值可以节省更多。这个增量值的增量值叫做delta-of-delta。

我们取上例时间戳的delta-of-delta。

对于第一个时间戳，由于无法计算增量值，我们按原样写入160000000。根据论文，Gorilla使用固定长度编码来编码数据，而tstorage使用一种称为Variants的可变长度编码方法。

对于第二个时间戳，因为delta-of-delta还无法计算，所以我们按原样写增量值60。因为Gorilla假设每4小时（=16384秒）创建一个时间序列数据块，可以获取的最大位数是14位，所以它用14位的固定长度进行编码。然而，tstorage使用Variants进行可变长度编码（Prometheus也使用Variants编码前两个时间戳，我实在不知道为什么Gorilla使用固定长度）。

如果你有兴趣了解更多Variants的工作原理，请查看我的上一篇文章：https://nakabonne.dev/posts/binary-encoding-go/#how-varints-works

delta-of-delta使用可变长度编码进行编码，因此它的大小取决于要写入的数字的大小。如果delta-of-delta为0，则使用1位写入0。如果delta-of-delta在64～64范围内，则使用2位写入1和0，然后使用7位写入delta-of-delta。

所以每个时间戳的大小是：

总大小为40+8+1+9=58位。

如果我们对原始的四个时间戳进行定长编码，则得到64 x 4=256位；可以看到我们节省了很多尺寸。

如你所见，如果时间戳以固定的间隔排列，那么delta-of-delta将始终为零，这使得编码非常高效。如果想保持尽可能小的尺寸，你应该尝试以固定周期写入数据点。

如果想更详细地了解它，我建议你阅读论文的4.1.1压缩时间戳。

3.XOR编码

XOR编码是一种对两个浮点值进行异或运算，并将其代替实际值写入的方法。

如果取接近值的异或，前导零和尾部零往往更多，而我们希望可以忽略要写入的大小。例如，如果我们取2.0和3.0的异或：

2.0 ^ 3.0 = 0000000000001000000000000000000000000000000000000000000000000000└leading 0s┘ └                      trailing 0s                        ┘

正如你所看到的，异或结果分为三个部分：

• 前导零（12位）
• 1（1位）
• 尾部零（51位）

• 如果与前一个值相同的异或

• 如果与前一个值不同的异或

• 如果有意义位与前一个值的不同

原文：https://corecursive.com/066-sqlite-with-richard-hipp/

• https://misfra.me/state-of-the-state-part-iii
• https://fabxc.org/tsdb/
• https://questdb.io/blog/2020/11/26/why-timeseries-data
• http://www.vldb.org/pvldb/vol8/p1816-teller.pdf
• https://blog.timescale.com/blog/time-series-compression-algorithms-explained

- EOF -

回复关键字“简明python ”，立即获取入门必备书籍《简明python教程》电子版
回复关键字“爬虫”，立即获取爬虫学习资料

推荐