小米面试：孔融找梨

大家好，我是道哥，今天我们来聊一道小米公司的面试题，看似不难，但也不会那么容易。题目如下：

有n个梨，并已知每个梨的重量(整数)，试判断是否有两个梨的重量之和等于给定的值。要求时间复杂度尽可能低。

一般来说，如果应聘者在这个问题上犹豫不决，那基本说明没有好好准备面试，多么典型的两数之和啊。

然而，当应聘者嘴中蹦出two sum这两个词之后，其实也不太好，因为面试官肯定知道你做过这个题目。

当遇到熟练的题目后，该怎么表现，这是很微妙的。不久前，在一句小饭局上我请教过一个面试官朋友。

他说了这样一句话：应聘者在面试过程中，如果遇到熟悉的题目，尽量不要让面试官察觉到你做过该题。

这个朋友说的是否有道理，今天我们不评论。接下来，我们循序渐进地一步一步来分析和解答这个题目。

思路一: 两层循环

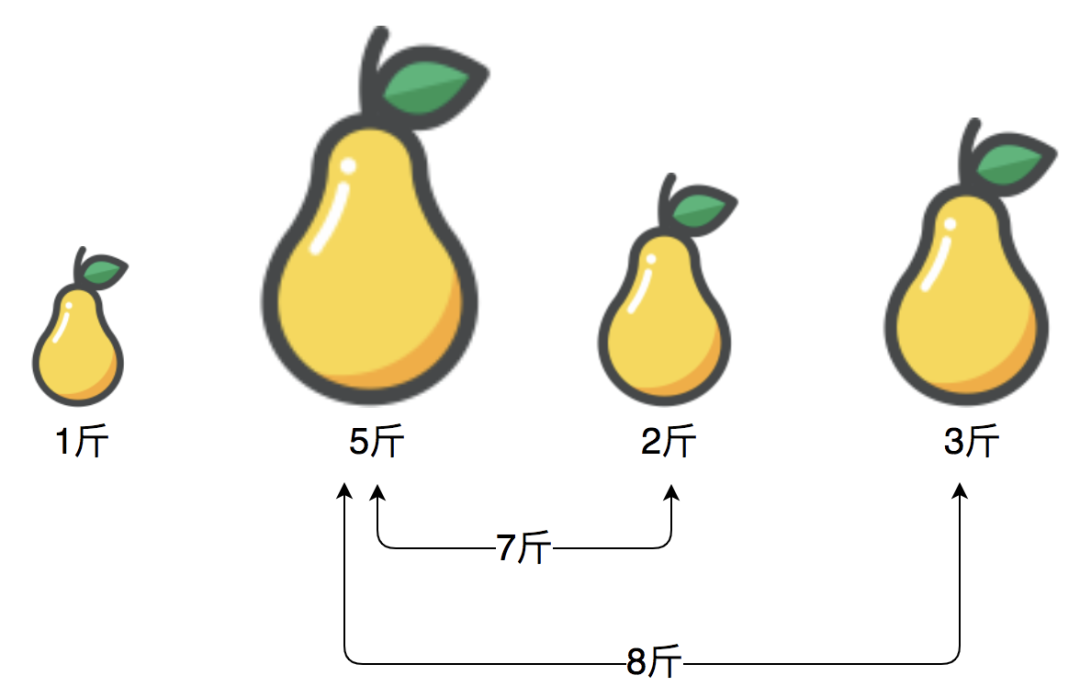
然后，以第三个梨为目标，继续向后查找，刚好能凑成5斤，终于找到了：

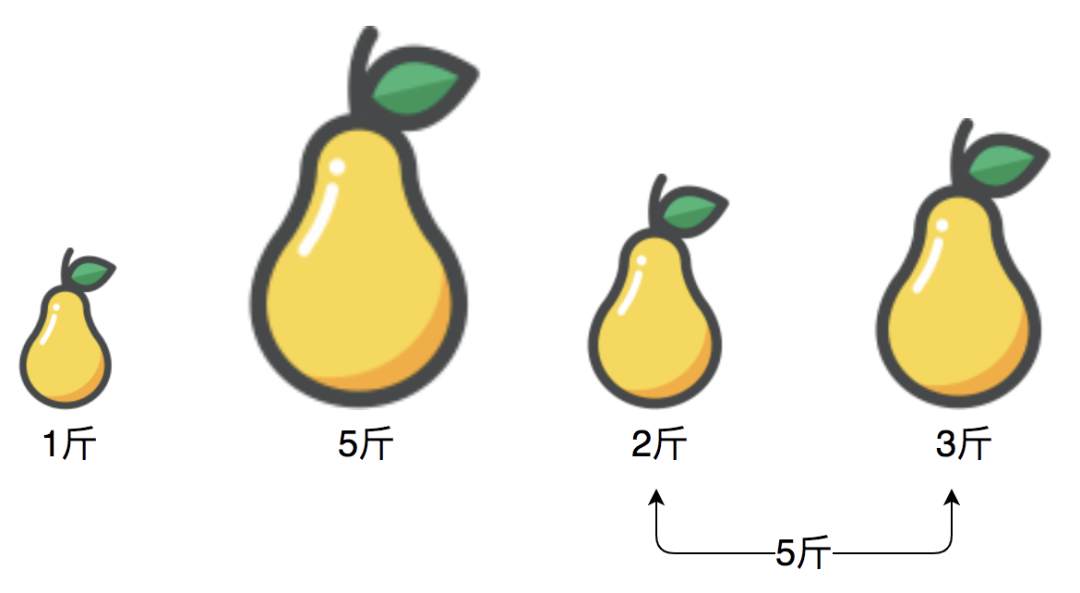
很显然，这里用到了两层循环，时间复杂度为O(N*N), 然而，我要说，这是不符合题目要求的，因为时间复杂度不是最优的。

思路二: 双指针法

接下来，我们对时间复杂度进行优化，先考虑对上述梨进行快速排序，时间复杂度为O(N*logN), 排序后的结果如下：

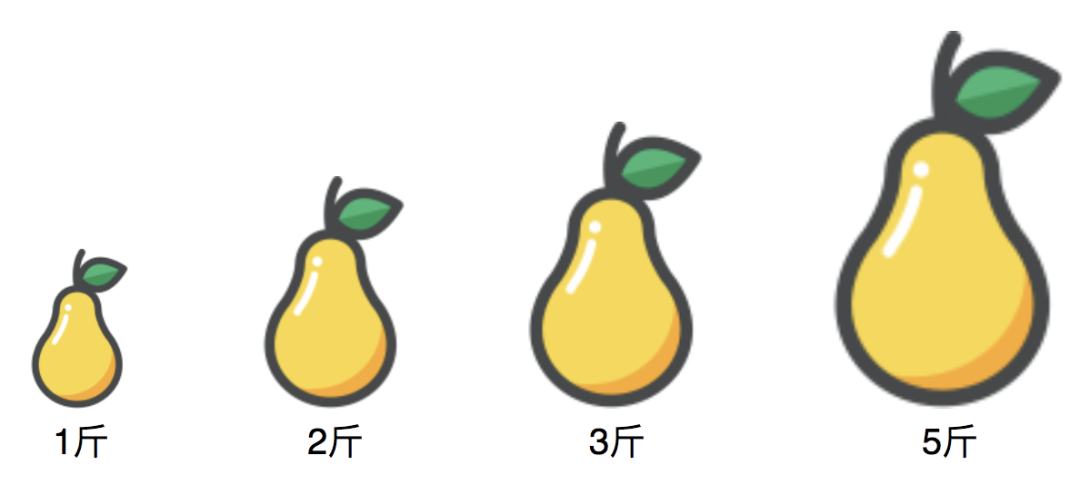
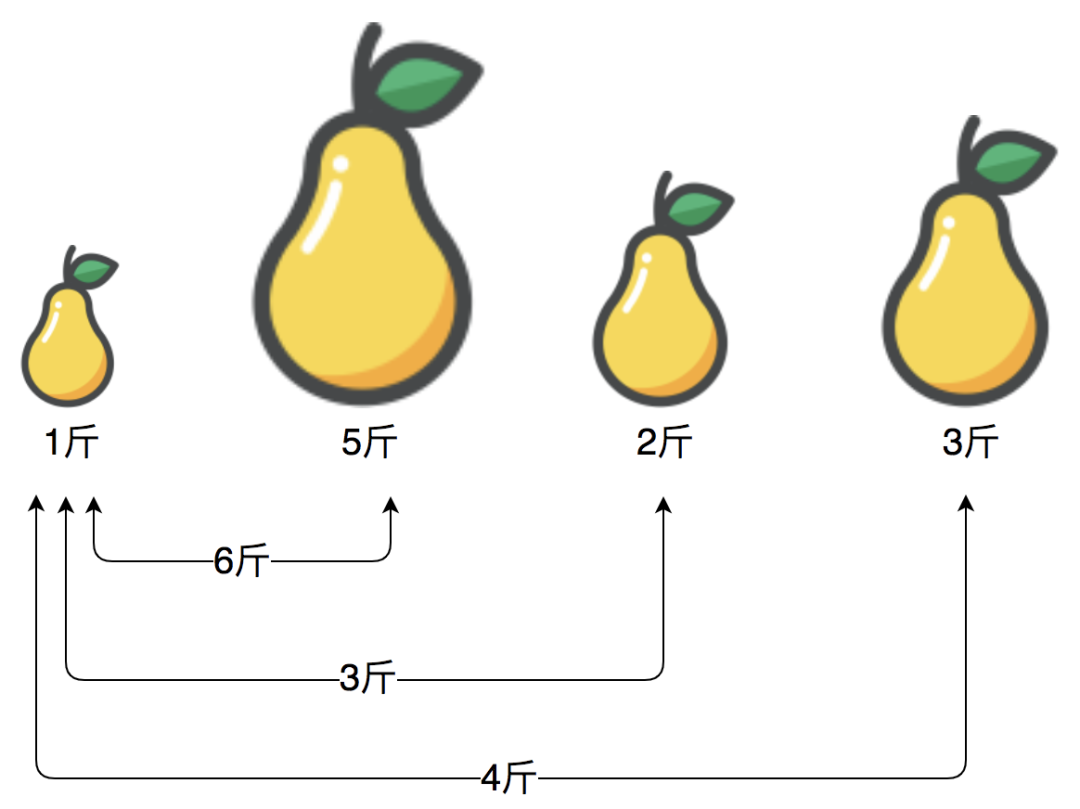
何为双指针呢？且看思路，我们观察第一个和最后一个梨，和为6：

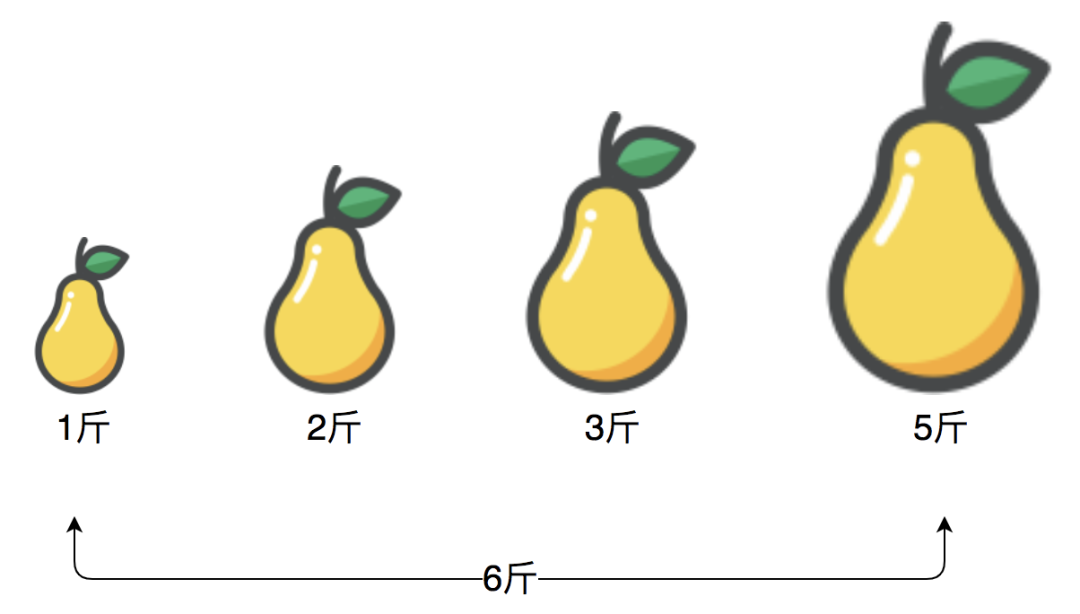
既然和为6，比咱们的目标5要大，那就必须要想办法缩小6的值，只能是右边的指针向左挪动来尝试，如下：

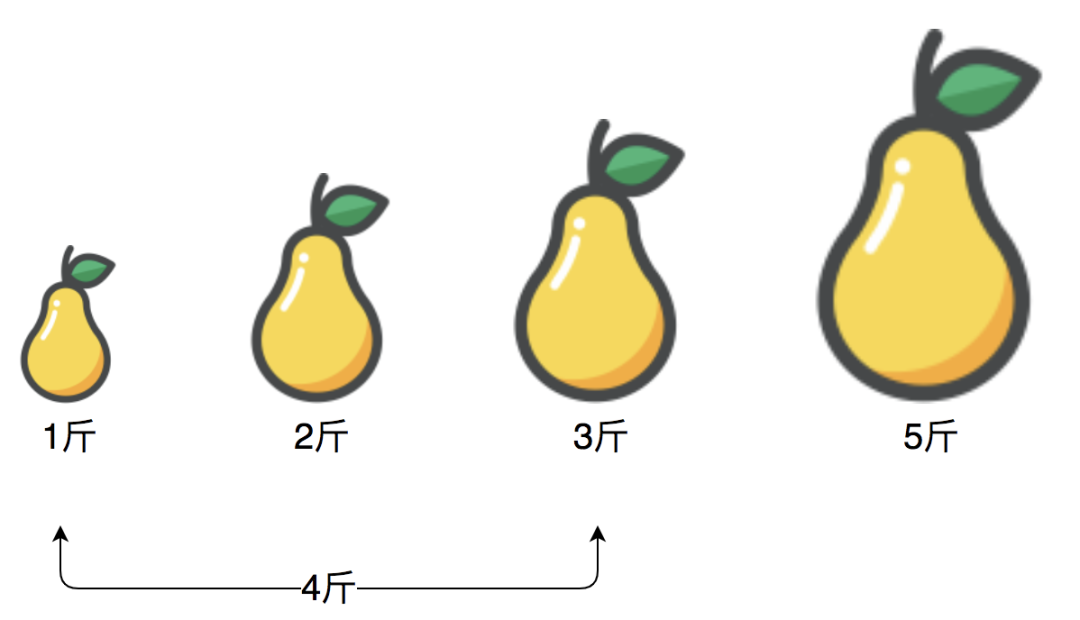
可以看到，上面两梨之和为4， 比咱们的目标5要小，所以必须想办法增大4，只能是左边的指针往右挪动来尝试，如下：

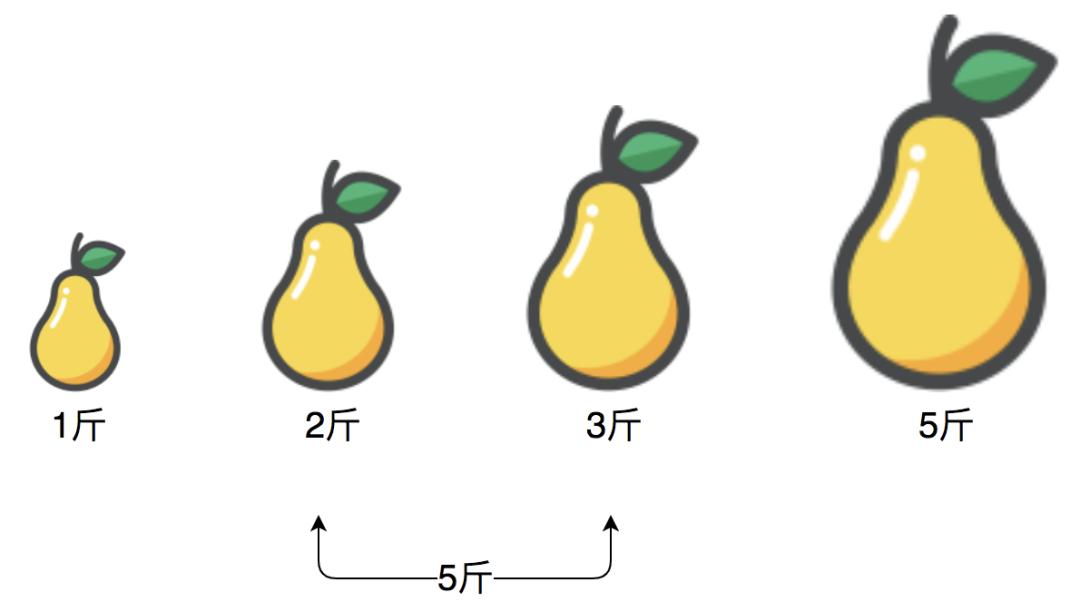
刚好，找到了和为5的两个梨，满足题目条件。此时，整个算法的时间复杂度取决于排序的时间复杂度，即为O(N*logN).

那么，这是最优的时间复杂度吗？显然不是。既然题目要求是时间复杂度最优，那么我们可以考虑以空间换时间，且往下看。

思路三: 哈希表法

我们来看下，以第一个梨为目标，它的重量是1斤，也就是说，接下来的任务就是要找到一个4斤的梨：

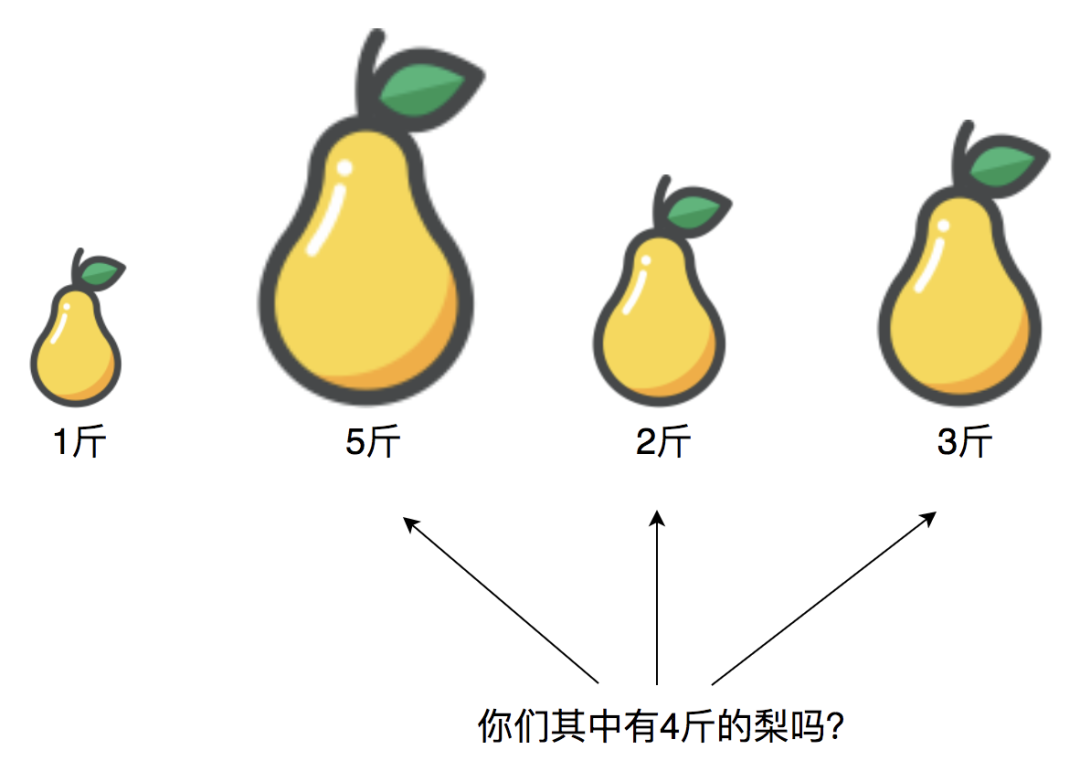
显然，查找4斤梨的过程，不要使用暴力遍历，而要使用哈希表，查找的时间复杂度为O(1)，最后发现没有4斤的梨。

接着，我们以第二个5斤的梨为目标，需要在剩余的梨中找到重量为0斤的梨，哈希查找的时间复杂度为O(1)，最后发现没有0斤的梨。

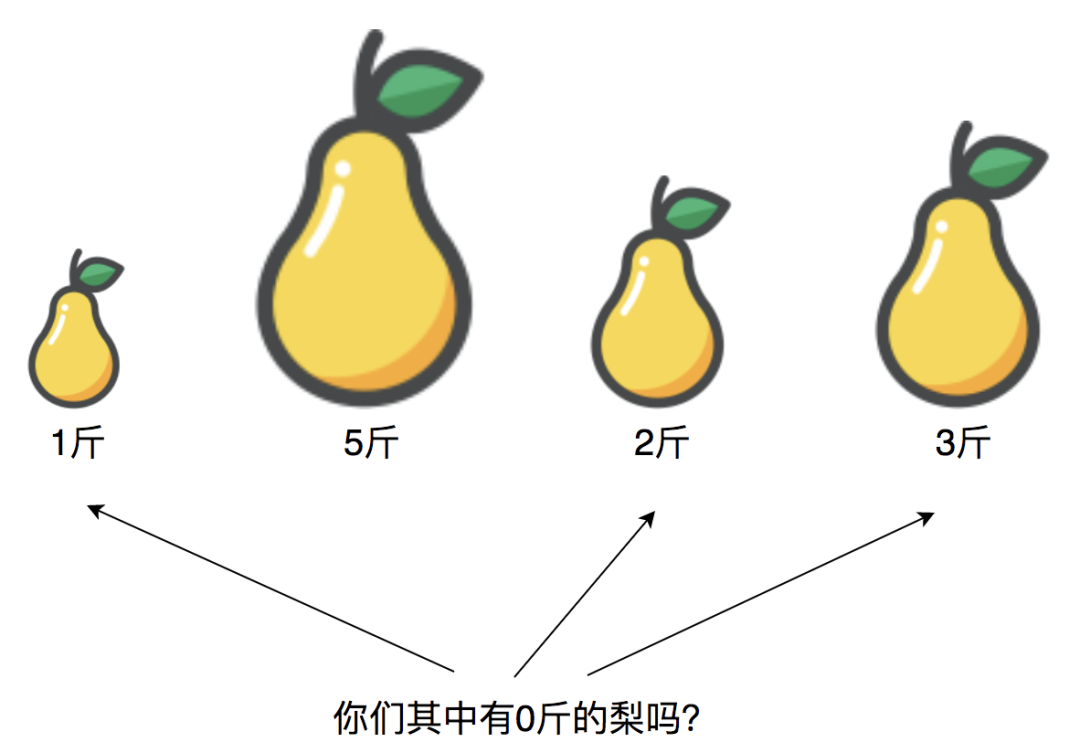
接下来，我们以第三个2斤的梨为目标，需要在剩余的梨中找到重量为3斤的梨，哈希查找的时间复杂度为O(1)，最后发现有3斤的梨，万事大吉啦：

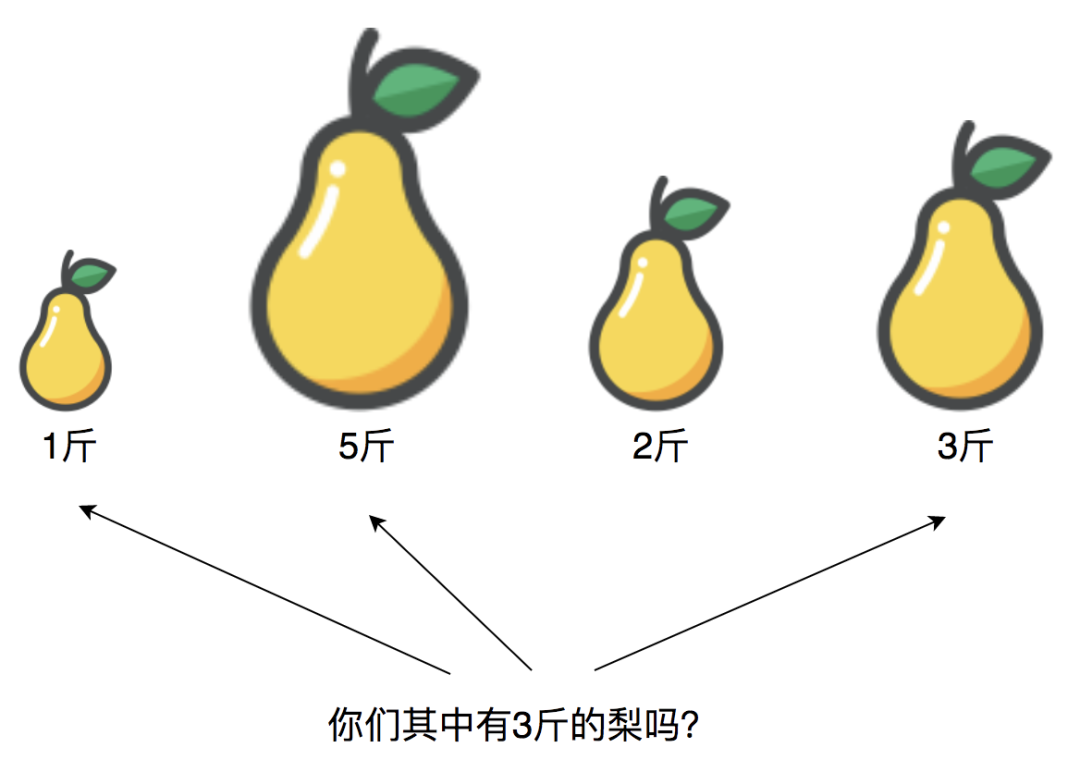
可以看到，整个算法过程的时间复杂度就是O(N)，是最优的时间复杂度，符合题目要求，能通过面试。

那么，该怎么来写程序呢？上次有个朋友说我偏爱C++的读者，哈哈，这次我用Golang语言来写程序。

要注意，Golang的map便于基于哈希表，经测试如下程序OK:

package mainimport "fmt"
func solution(nums []int, target int) bool {    m := make(map[int]int)    lenN := len(nums)    for i, v := range nums {        m[v] = i    }
    for i := 0; i <  lenN; i++ {        if j, ok := m[target - nums[i]]; ok && i < j {            return true        }    }
    return false}
func main() {  fmt.Println(solution([]int{1, 5, 2, 3}, 5))   // true  fmt.Println(solution([]int{1, 5, 2, 3}, 10))  // false}