涨知识: Python计算0.1+0.2≠0.3?

作者：武沛齐  

出处：http://www.cnblogs.com/wupeiqi/

本文版权归作者和博客园共有

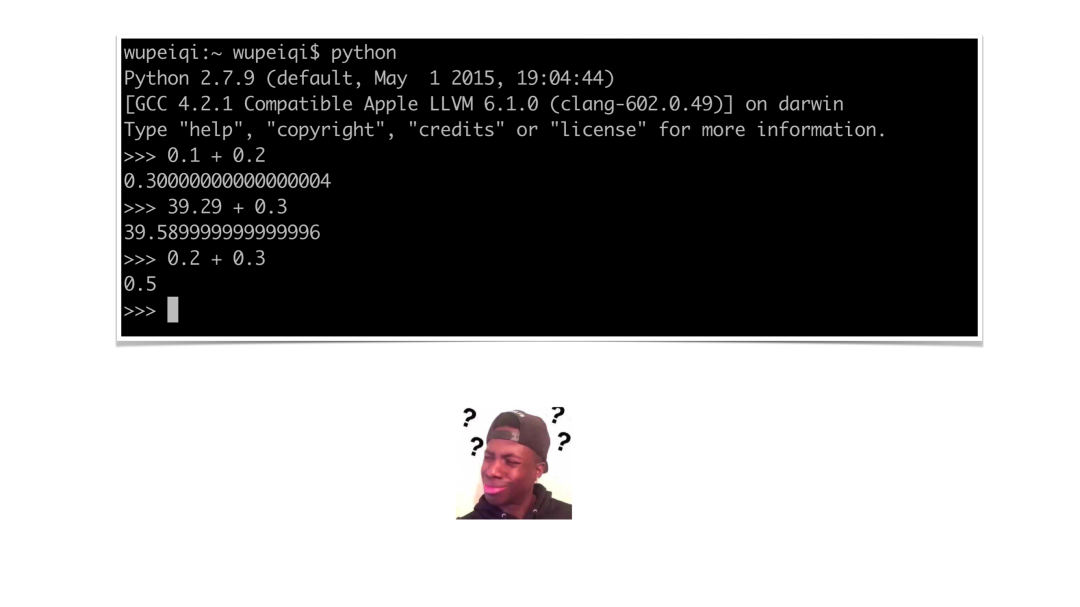
为啥会有上述图片的现象呢？其实是由于float底层存储原理导致，下面听我娓娓道来。

第一步：浮点数转换为二进制表示

• 整数部分，直接转换为二进制，即：`100111`

• 小数部分，让小数一直乘2，小于1则用结果继续乘，大于1则结果减1继续乘，等于1则结束。

如果小数位是0.25就会比较简单，例如：
0.25 * 2 = 0.5 // 小于1，则继续乘
0.5 * 2 = 1 // 等于1，则结束
结束时，将相乘之后等结果的整数部分拼接起来，所以 0.25 的二进制表示：01

第二步：科学计数法表示二进制小数

注意：因为是二进制小数，所以底数是2。

第三步：存储

• Float32，用32位的二进制来存储一个浮点数。

• Float64，用64位的二进制来存储一个浮点数。

接下来，我们以float32为例：

通过对浮点型的存储原理的学习，了解到浮点型其实是一种非精确的表达小数的方式，因为他的fraction中有位数限制，超过就会忽略。

float64和float32类似，只是用于表示各部分的位数不同而已，其中：`sign=1位`、`exponent=11位`、`fraction=52位`，也就意味着可以表示的范围更大了。

总结

在开发中想精确的处理小数时，可以使用decimal。

扫一扫下面的二维码免费领取10G的Python学习资料哦~

“扫一扫，领取Python学习资料”