告警:线上慎用 BigDecimal ,坑的差点被开了...
BigDecimal,相信对于很多人来说都不陌生,很多人都知道他的用法,这是一种java.math包中提供的一种可以用来进行精确运算的类型。
很多人都知道,在进行金额表示、金额计算等场景,不能使用double、float等类型,而是要使用对精度支持的更好的BigDecimal。
所以,很多支付、电商、金融等业务中,BigDecimal的使用非常频繁。但是,如果误以为只要使用BigDecimal表示数字,结果就一定精确,那就大错特错了!
在之前的一篇文章中,我们介绍过,使用BigDecimal的equals方法并不能验证两个数是否真的相等(为什么阿里巴巴禁止使用BigDecimal的equals方法做等值比较?)。
除了这个情况,BigDecimal的使用的第一步就是创建一个BigDecimal对象,如果这一步都有问题,那么后面怎么算都是错的!
那到底应该如何正确的创建一个BigDecimal?
关于这个问题,我Review过很多代码,也面试过很多一线开发,很多人都掉进坑里过。这是一个很容易被忽略,但是又影响重大的问题。
关于这个问题,在《阿里巴巴Java开发手册》中有一条建议,或者说是要求:

这是一条【强制】建议,那么,这背后的原理是什么呢?
想要搞清楚这个问题,主要需要弄清楚以下几个问题:
1、为什么说double不精确?
2、BigDecimal是如何保证精确的?
在知道这两个问题的答案之后,我们也就大概知道为什么不能使用BigDecimal(double)来创建一个BigDecimal了。
double为什么不精确
首先,计算机是只认识二进制的,即0和1,这个大家一定都知道。
那么,所有数字,包括整数和小数,想要在计算机中存储和展示,都需要转成二进制。
十进制整数转成二进制很简单,通常采用"除2取余,逆序排列"即可,如10的二进制为1010。
但是,小数的二进制如何表示呢?
十进制小数转成二进制,一般采用"乘2取整,顺序排列"方法,如0.625转成二进制的表示为0.101。
但是,并不是所有小数都能转成二进制,如0.1就不能直接用二进制表示,他的二进制是0.000110011001100… 这是一个无限循环小数。
所以,计算机是没办法用二进制精确的表示0.1的。也就是说,在计算机中,很多小数没办法精确的使用二进制表示出来。
那么,这个问题总要解决吧。那么,人们想出了一种采用一定的精度,使用近似值表示一个小数的办法。这就是IEEE 754(IEEE二进制浮点数算术标准)规范的主要思想。
IEEE 754规定了多种表示浮点数值的方式,其中最常用的就是32位单精度浮点数和64位双精度浮点数。
在Java中,使用float和double分别用来表示单精度浮点数和双精度浮点数。
所谓精度不同,可以简单的理解为保留有效位数不同。采用保留有效位数的方式近似的表示小数。
所以,大家也就知道为什么double表示的小数不精确了。
接下来,再回到BigDecimal的介绍,我们接下来看看是如何表示一个数的,他如何保证精确呢?
BigDecimal如何精确计数?
如果大家看过BigDecimal的源码,其实可以发现,实际上一个BigDecimal是通过一个"无标度值"和一个"标度"来表示一个数的。
在BigDecimal中,标度是通过scale字段来表示的。
而无标度值的表示比较复杂。当unscaled value超过阈值(默认为Long.MAX_VALUE)时采用intVal字段存储unscaled value,intCompact字段存储Long.MIN_VALUE,否则对unscaled value进行压缩存储到long型的intCompact字段用于后续计算,intVal为空。
涉及到的字段就是这几个:
public class BigDecimal extends Number implements Comparable<BigDecimal> {
private final BigInteger intVal;
private final int scale;
private final transient long intCompact;
}
关于无标度值的压缩机制大家了解即可,不是本文的重点,大家只需要知道BigDecimal主要是通过一个无标度值和标度来表示的就行了。
那么标度到底是什么呢?
除了scale这个字段,在BigDecimal中还提供了scale()方法,用来返回这个BigDecimal的标度。
/**
* Returns the <i>scale</i> of this {@code BigDecimal}. If zero
* or positive, the scale is the number of digits to the right of
* the decimal point. If negative, the unscaled value of the
* number is multiplied by ten to the power of the negation of the
* scale. For example, a scale of {@code -3} means the unscaled
* value is multiplied by 1000.
*
* @return the scale of this {@code BigDecimal}.
*/
public int scale(){
return scale;
}
那么,scale到底表示的是什么,其实上面的注释已经说的很清楚了:
如果scale为零或正值,则该值表示这个数字小数点右侧的位数。如果scale为负数,则该数字的真实值需要乘以10的该负数的绝对值的幂。例如,scale为-3,则这个数需要乘1000,即在末尾有3个0。
如123.123,那么如果使用BigDecimal表示,那么他的无标度值为123123,他的标度为3。
而二进制无法表示的0.1,使用BigDecimal就可以表示了,及通过无标度值1和标度1来表示。
我们都知道,想要创建一个对象,需要使用该类的构造方法,在BigDecimal中一共有以下4个构造方法:
BigDecimal(int)
BigDecimal(double)
BigDecimal(long)
BigDecimal(String)
以上四个方法,创建出来的的BigDecimal的标度(scale)是不同的。
其中 BigDecimal(int)和BigDecimal(long) 比较简单,因为都是整数,所以他们的标度都是0。
而BigDecimal(double) 和BigDecimal(String)的标度就有很多学问了。
BigDecimal(double)有什么问题
BigDecimal中提供了一个通过double创建BigDecimal的方法——BigDecimal(double) ,但是,同时也给我们留了一个坑!
因为我们知道,double表示的小数是不精确的,如0.1这个数字,double只能表示他的近似值。
所以,当我们使用new BigDecimal(0.1)创建一个BigDecimal 的时候,其实创建出来的值并不是正好等于0.1的。
而是0.1000000000000000055511151231257827021181583404541015625。这是因为doule自身表示的只是一个近似值。
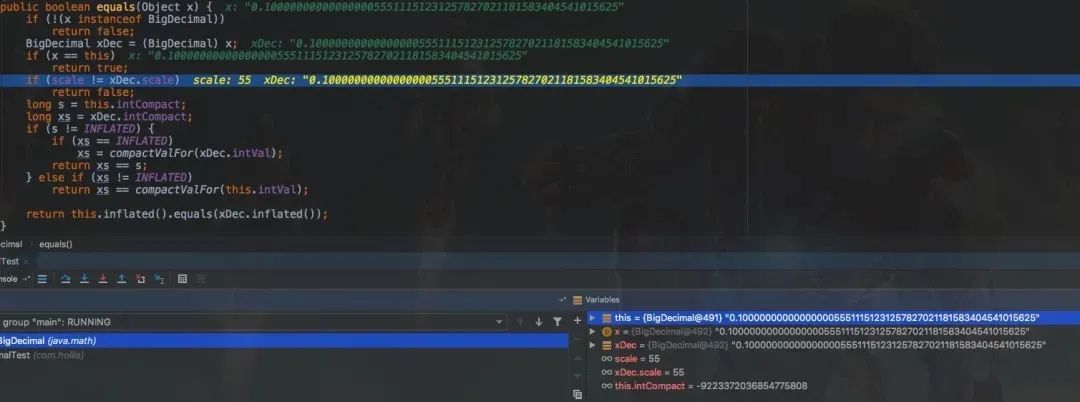
所以,如果我们在代码中,使用BigDecimal(double) 来创建一个BigDecimal的话,那么是损失了精度的,这是极其严重的。
使用BigDecimal(String)创建
那么,该如何创建一个精确的BigDecimal来表示小数呢,答案是使用String创建。
而对于BigDecimal(String) ,当我们使用new BigDecimal("0.1")创建一个BigDecimal 的时候,其实创建出来的值正好就是等于0.1的。
那么他的标度也就是1。
但是需要注意的是,new BigDecimal("0.10000")和new BigDecimal("0.1")这两个数的标度分别是5和1,如果使用BigDecimal的equals方法比较,得到的结果是false,具体原因和解决办法参考为什么阿里巴巴禁止使用BigDecimal的equals方法做等值比较?
那么,想要创建一个能精确的表示0.1的BigDecimal,请使用以下两种方式:
BigDecimal recommend1 = new BigDecimal("0.1");
BigDecimal recommend2 = BigDecimal.valueOf(0.1);
这里,留一个思考题,BigDecimal.valueOf()是调用Double.toString方法实现的,那么,既然double都是不精确的,BigDecimal.valueOf(0.1)怎么保证精确呢?
总结
因为计算机采用二进制处理数据,但是很多小数,如0.1的二进制是一个无线循环小数,而这种数字在计算机中是无法精确表示的。
所以,人们采用了一种通过近似值的方式在计算机中表示,于是就有了单精度浮点数和双精度浮点数等。
所以,作为单精度浮点数的float和双精度浮点数的double,在表示小数的时候只是近似值,并不是真实值。
所以,当使用BigDecimal(Double)创建一个的时候,得到的BigDecimal是损失了精度的。
而使用一个损失了精度的数字进行计算,得到的结果也是不精确的。
想要避免这个问题,可以通过BigDecimal(String)的方式创建BigDecimal,这样的情况下,0.1就会被精确的表示出来。
其表现形式是一个无标度数值1,和一个标度1的组合。
程序汪资料链接
卧槽!字节跳动《算法中文手册》火了,完整版 PDF 开放下载!
卧槽!阿里大佬总结的《图解Java》火了,完整版PDF开放下载!
欢迎添加程序汪个人微信 itwang009 进粉丝群或围观朋友圈

