单身男女问题的科学解决方案



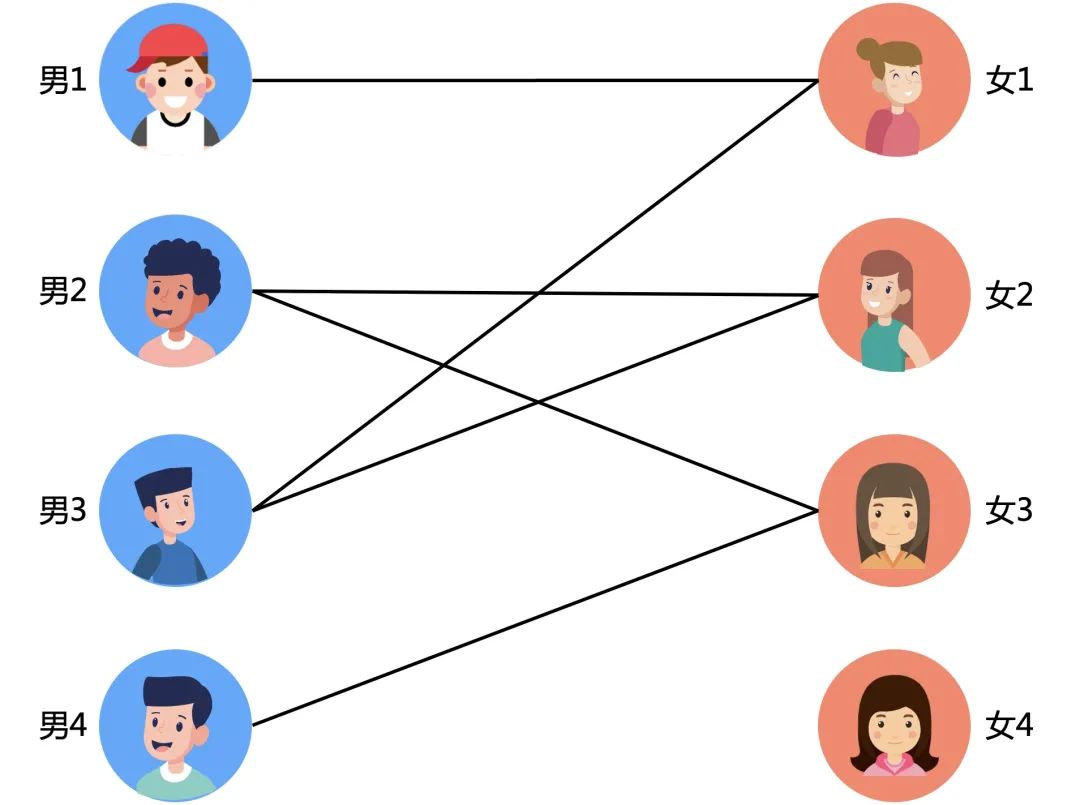



于是对女2号发起了进攻。


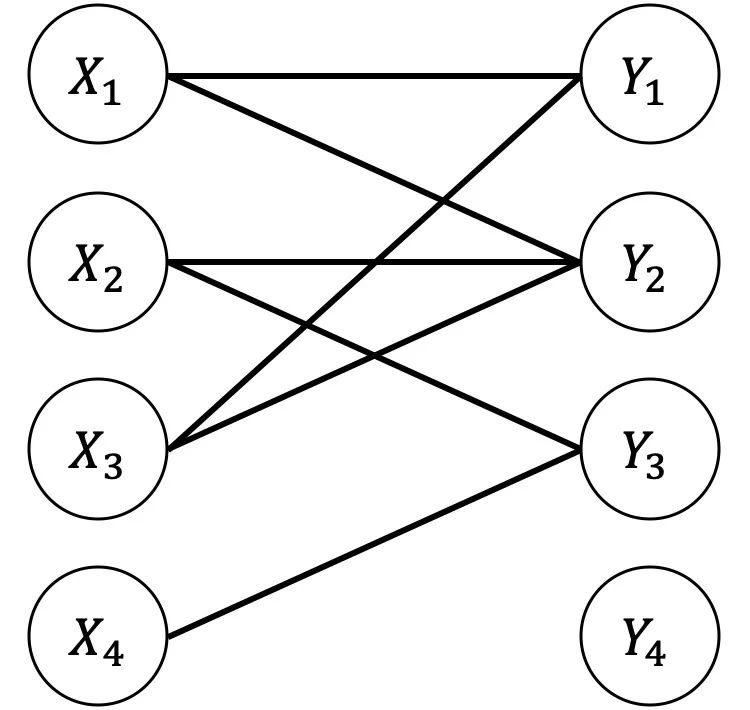
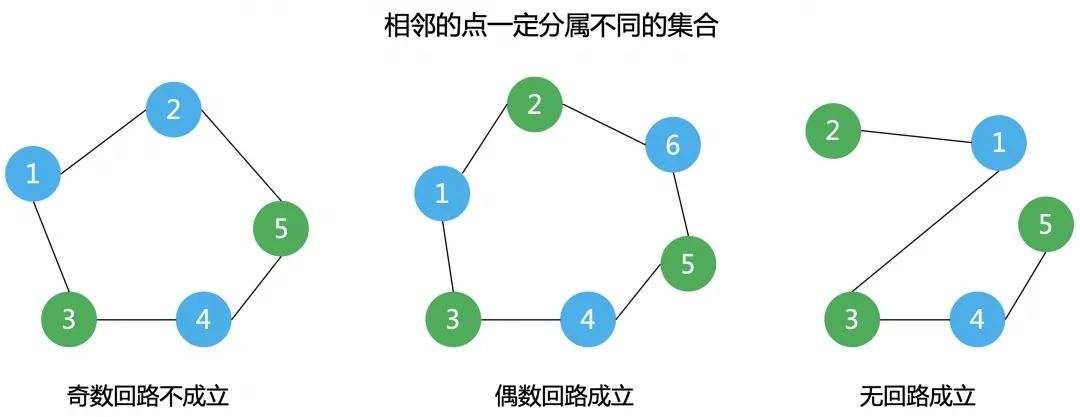
判断方法:染色法
开始对任意一未染色的顶点染色 判断其相邻的顶点中,若未染色则将其染上和相邻顶点不同的颜色; 若已经染色且颜色和相邻顶点的颜色相同则说明不是二分图,若颜色不同则继续判断
在二分图G的子图M中,M的边集E中的任意两条边都不依附于同一个顶点,则称M是一个匹配。
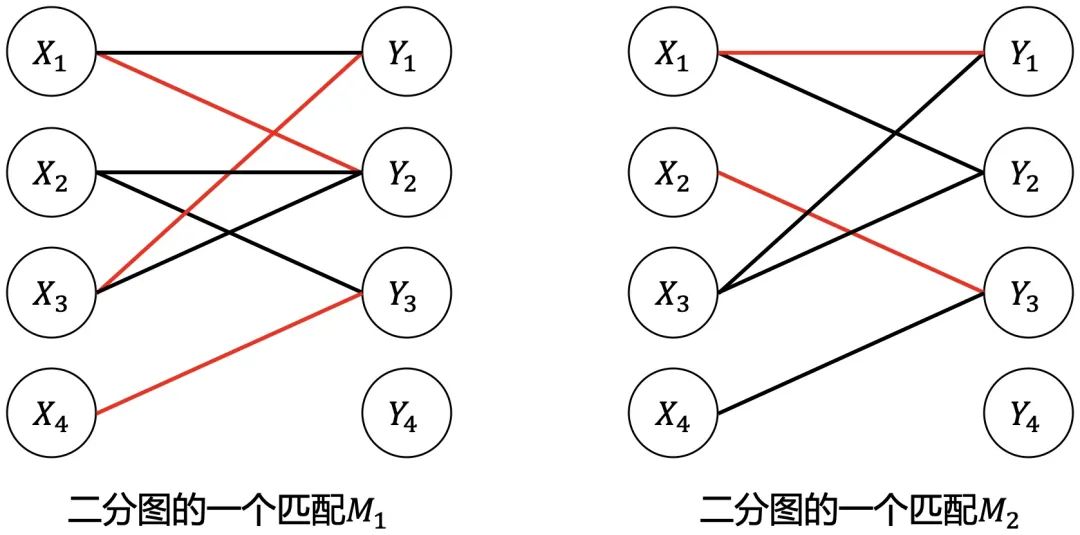
匹配M的边集所关联的点为饱和点,否则为非饱和点。如上图:
的饱和点:。 的饱和点:。
定义:图G的一条路径,且路径中的边在属于M和不属于M中交替出现。
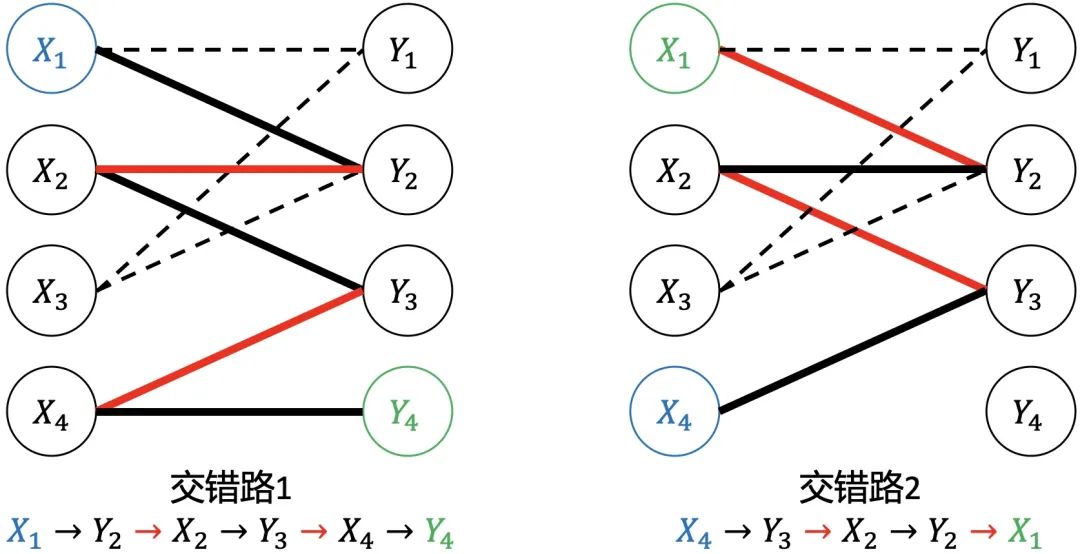
定义:一条交错路,且该交错路的起点和终点都为匹配M的非饱和点。
如上图,交错路1是增广路;交错路2不是增广路,因为终点不是非饱和点。
路径的边数为奇数,第一条边和最后一条边都不属于M 将路径中的边的匹配方式取反操作,会得到更大的匹配M',匹配数加1 M为图G的最大匹配等价于不存在M的增广路
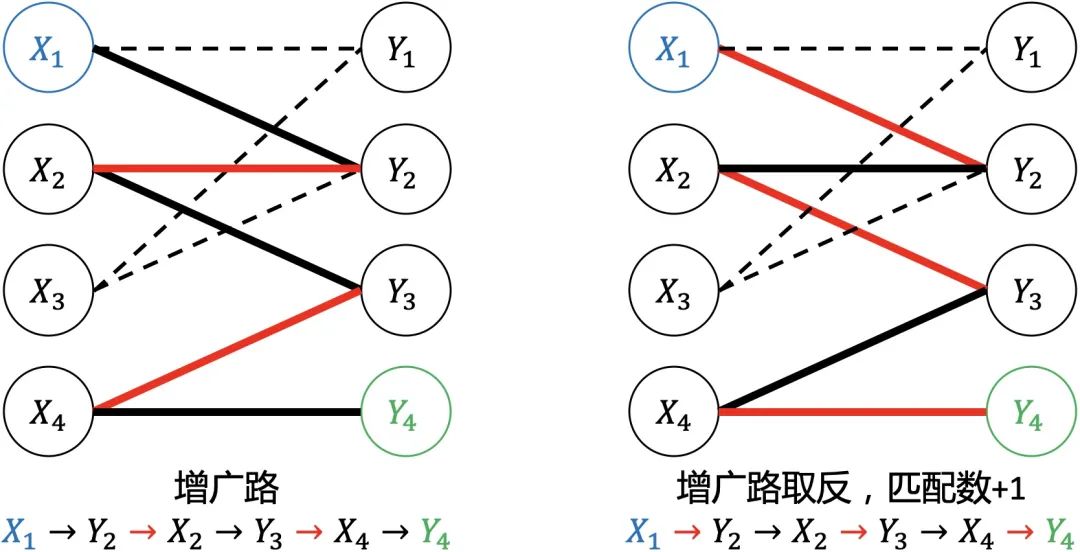
1) 初始匹配M为空 2) 找出一条增广路径p,取反操作得到更大的匹配M'代替M 3) 重复步骤2),直到找不出增广路为止
const int MAXM = 200, MAXN = 200;
bool map[MAXN][MAXM] = {false}, visit[MAXM];
int n, m, x[MAXM], y[MAXN], ans = 0;
void init() {
memset(x, 0xff, MAXM * 4);
memset(y, 0xff, MAXN * 4);
memset(map, false, MAXN * MAXM);
int num, temp;
cin >> n >> m;
for (int i = 0; i < n; ++i) {
cin >> num;
for (int j = 0; j < num; ++j) {
cin >> temp;
map[i][temp - 1] = true;
}
}
}
bool hungary(int u) {
for (int i = 0; i < m; ++i) {
if (!visit[i] && map[u][i]) {
visit[i] = true;
if (y[i] == -1 || hungary(y[i])) {
x[u] = i;
y[i] = u;
return true;
}
}
}
return false;
}
int main() {
init();
for (int i = 0; i < n; ++i) {
if (x[i] == -1) {
memset(visit, false, MAXM);
if (hungary(i)) {
ans++;
}
}
}
cout << ans << endl;
return 0;
}
输入
5 5
2 2 5
3 2 3 4
2 1 5
3 1 2 5
1 2
输出
4


评论

