.NET中对数据库友好的GUID的变种使用方法
概述
.NET生成的GUID唯一性很好,用之方便,但是,缺少像雪花算法那样的有序性。虽然分布式系统中做不到绝对的有序,但是,相对的有序对于目前数据库而言,索引效率等方面的提升还是有明显效果的(当然,我认为,这是数据库的问题,而非编程的问题,数据库应该处理好任何类型数据作为主键索引时的性能,除非在SQL标准中明确写不支持哪些数据类型)。
在当前数据库无法解决这些问题的时候,除了使用雪花算法,是否能够改造GUID,利用微软已经相当成熟的GUID的性能与效率的同时,加上序列的特性呢。本文就是做此尝试。
GUID与雪花算法
个人主观的感受,雪花算法生成简单,但是,在生产环境配置需要注意,同时,有范围限制(时间、数据中心、工作机器、单位时间生成个数都有限制),正常情况下,这些范围足够使用,但是,毕竟GUID是没有限制的,唯一的问题就是有极低的概念会重复,这种重复在插入的时候,通过数据库的Pk是可以及时发现并处理的,不会产生生产故障。
claus是这样评价这两个算法的:
GUID 和 Snowflake 都是常见的唯一ID生成方案,主要有以下区别:
优点:
1、GUID是完全随机的,碰撞概率极低,唯一性非常好。
2、GUID不依赖中心节点,分布式环境下也能生成,更适合于分布式系统。
3、GUID包含版本信息,可以对不同算法生成的GUID进行区分,向下兼容。
缺点:
1、GUID是无序的,不能进行排序,对数据库索引不友好。
2、GUID较长,作为主键会占用更多存储空间。
3、GUID包含 BPSK 码,大小写字母和短划线,可读性较差。
Snowflake算法:
优点:
1、可以按时间有序生成ID,对数据库索引更友好。
2、整体ID更短小,节省存储空间。
3、不包含特殊字符,可读性更好。
缺点:
1、依赖中心节点时间戳,必须保证节点时间同步。
2、不适合大规模分布式环境,扩展性较弱。
3、序列号周期较短,需要自定义优化。
4、不向下兼容,算法变更会导致ID不连续。
总之,应根据分布式需求、时间序需求、存储空间和可读性等进行权衡选择。
我们需要用到时间值
(戳?还是不蹭UNIX的概念吧)
1 毫秒=1000000 纳秒
var dt = DateTime.Now;// 当前时间
Console.WriteLine(dt.Ticks);// 638322150575422659,这是.net自带的运算,其它语言可以使用下面的方式生成。
Console.WriteLine((dt - new DateTime(1, 1, 1)).TotalMilliseconds*10000); // 638322150575422700
// 通过Ticks,可以取得100ns,即万分之一毫秒的精度。到3023年(1千年以后),Ticks的值也不会进位,其值为953650368000000000。
了解一下GUID
GUID 的格式为“xxxxxxxx-xxxx-xxxx-xxxx-xxxxxxxxxxxx”。
其含义为:【时间值低位 32bit】-【时间值中位 16bit】-【版本号 4bit】【时间值高位 4bit】【时间值高位 8bit】-【变体值 2bit】【时间序列高位 6bit】-【节点值 48bit】
位数为:8hex-4hex-4hex-4hex-12hex。
var uuidN = Guid.NewGuid().ToString("N"); // e0a953c3ee6040eaa9fae2b667060e09时间值+GUID
时间值本身是一个long类型的数字,其大小为Int64,即8byte。
guid本身就是一个byte[],其长度为16位。
所以,我们生成一个byte[],前8位放时间值,后面放GUID,在比较大小的时候,前端的位置优先级更高,所以,后面的GUID的无序特性会被覆盖。
| 8 位 Byte | 8 位 Byte | 8 位 Byte |
|---|---|---|
| 时间值 | GUID值 |
加在一起,一共24个字节。
Base64字符串化
因为数据库、前端、CSV等环境下,无法描述所有的Byte(原因是部分AscII是非可见字符),故而,需要将其进行类似Base64的转换。
转换后,我们会得到一个长度大概24/3*4=32位长度的字符串。这个字符串的字节数至少是32,但是,其具体更好的可读性。
但是,Base64有一个缺陷,我们来看一下它的码表:
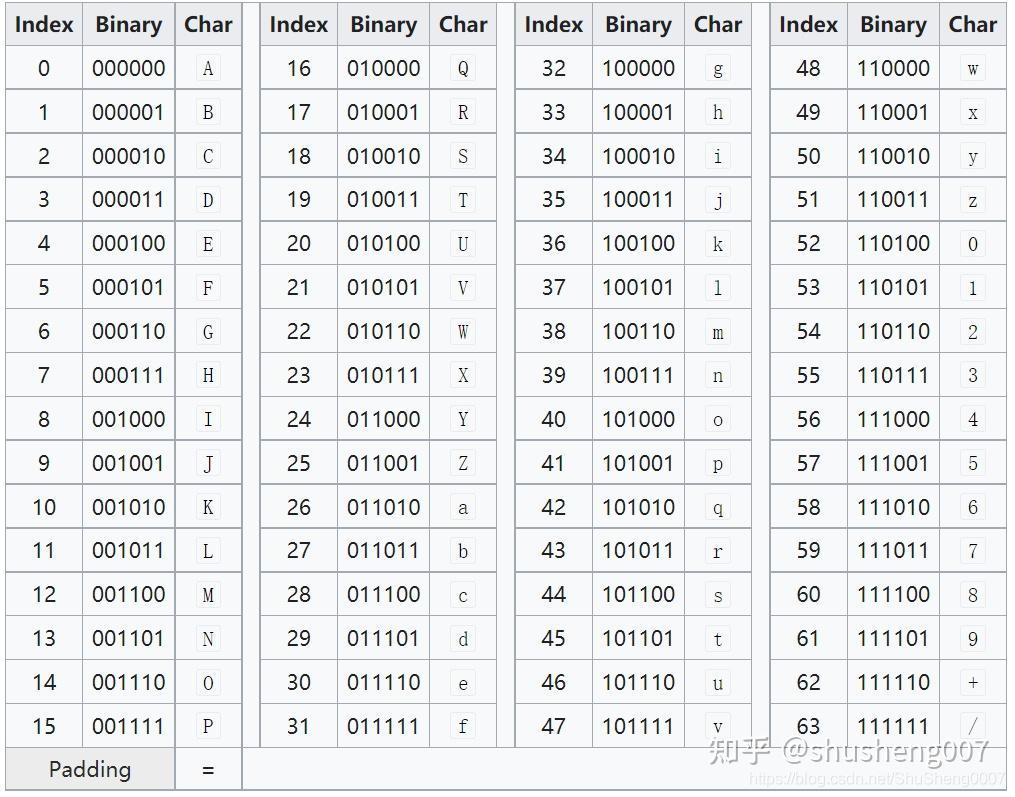
可以看到,【大写字母】<【小写字母】<【数字】<【+】<【/】。
但是,我们的程序进行比较时,并非如此,而是遵循了AscII码表的次序。我们来看一下AscII码表的次序:
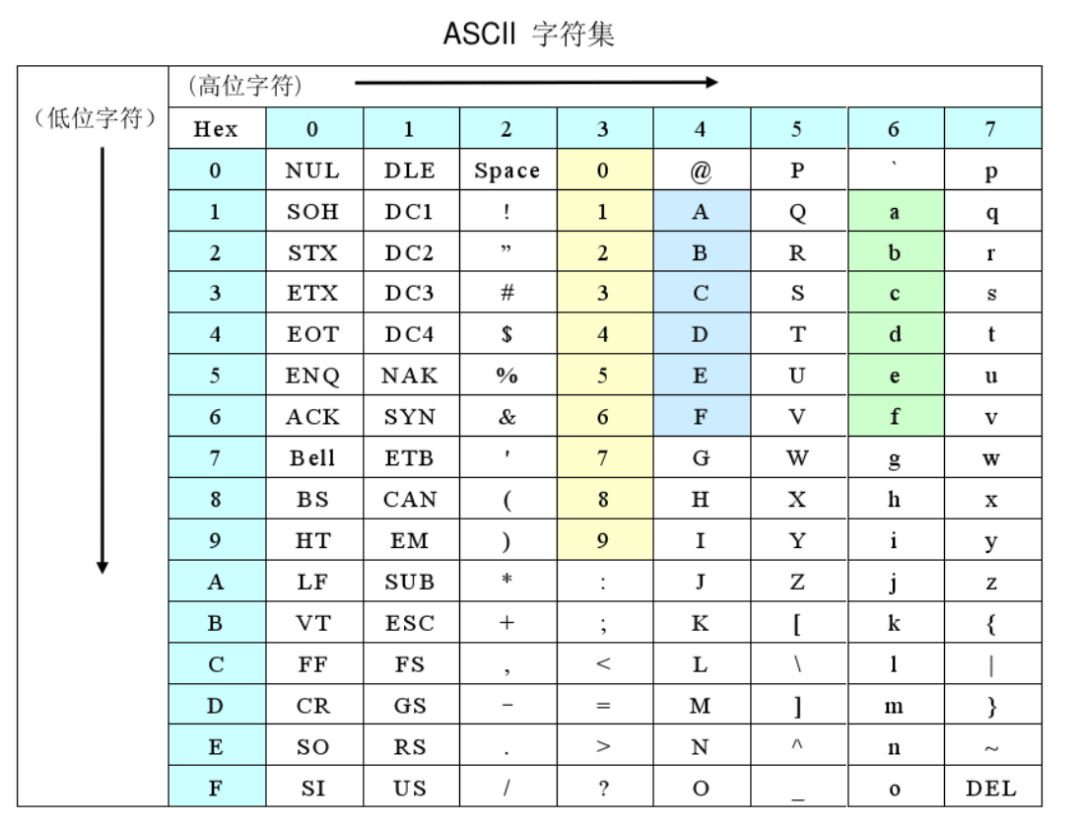
在AscII码表中,【/】<【数字】<【=】<【大写字母】<【小写字母】。
与上面的base64对比可以发现,如果我们将两串二进制用base64表示,则他们将无法使用base64字面的字符进行大小比较。所以,我们需要对base64进行一次转换,转换的结果要与ascii对应,起到和ascii大小次序一次的效果。
BaseSortValue-BSV
为了解决这个问题,我们需要将base64的二进制拿出来,然后, 给予他们有次序的新的码表即可。
但是,我们要做更长远的考虑,我们的BSV大概率会被用作主键,会用来查询,用出现在URL中,所以,我们应该避开URL的字义字符。URL的转义表如下:
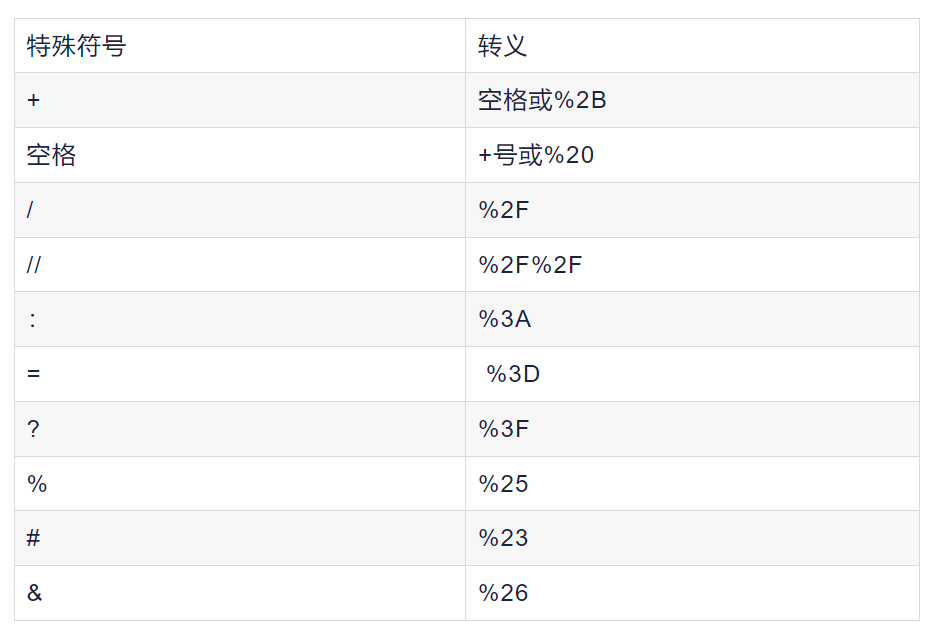
除了大小写字母、数字以外,我们还需要3个字符。除去URL转义字符,ASCII中可用的可视字符只剩下 !"$'()*,-.;<>[\]^_{|}~。其中"'出现在代码中容易影响代码本身的转义,故而不可。
_符号在查询时,经常因为疏忽看不见。
所以,最好的应该是!$-。因为这三者的中英文区别较大,具有较高的可识别度。同时,!小于数字及字母,作为补位可以不影响大小。最终形成的码表如下:
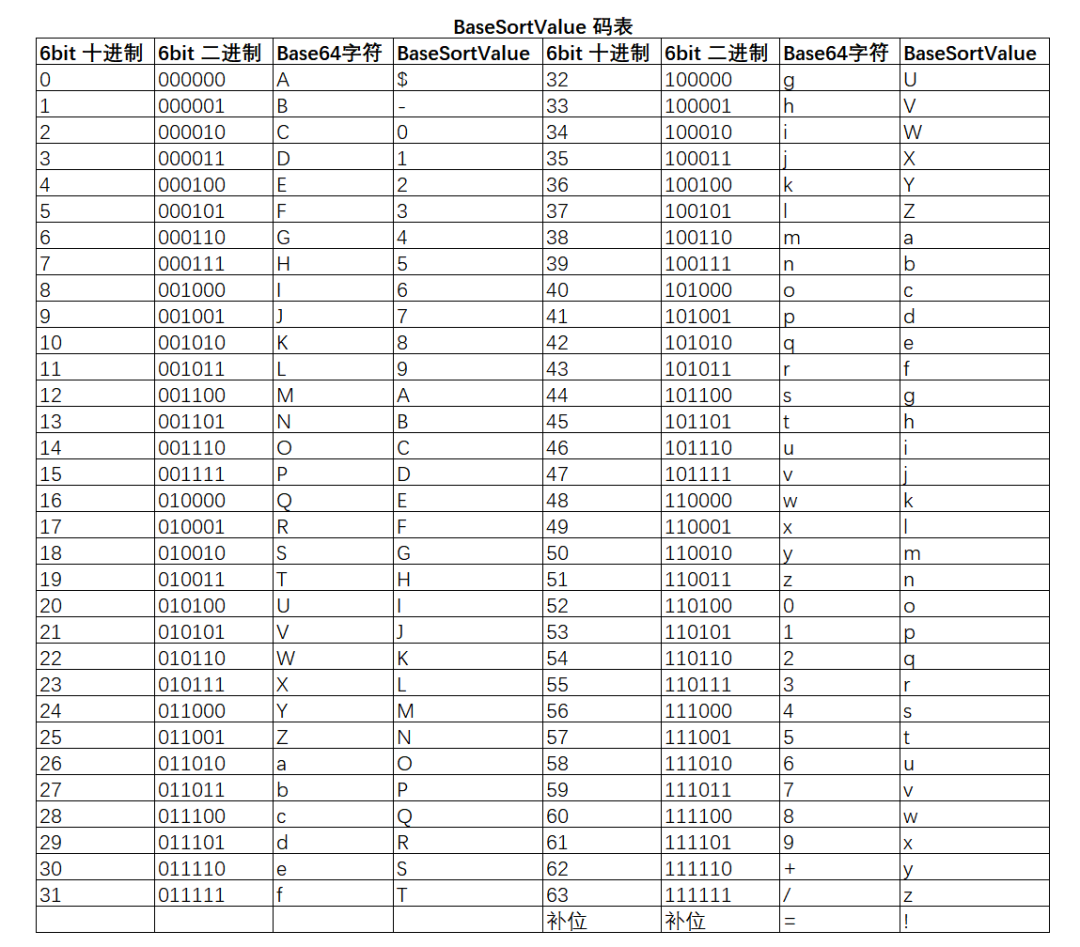
生成的结果如下:
0Bj4hRXIFkDoc$DXPivPF7nPBmO-smcF
0Bj4hU4f674ny-f0keZnG6VpDZm1b75r
0Bj4hU4h3WXnCsIKnnrrG7LHBzpH4yMF
0Bj4hU4h4FhniG-wH57BF6pSCVD$5sGp
0Bj4hU4h4Za$B5tkH2sIEtjA39M-nGuQ
0Bj4hU4h4qL0M-4nKRLZFcrU8qF$yezv
0Bj4hU4h548bDgf6ypAiFvI-HQSzZFeH
0Bj4hU4h5I47IsKrnkfdF7bfvOjMXWXm
0Bj4hU4h5V3P7fTSP0lBEcbZbF5h2CXV
0Bj4hU4h5iCiT-m$R7PfEeko7oaFcIPO
0Bj4hU4h5vDF6VNYTDSSFsHi1FUQt93p实现 - .NET
public static class SeqGuid
{
/// <summary>
/// 生成BSV的GUID。
/// </summary>
/// <returns></returns>
public static string NewGuid()
{
var gid = Guid.NewGuid().ToByteArray();// 获取唯一的guid,对应uuid的版本应该是v4。此处直接获取其byte数组。
var dtvalue = DateTime.Now.Ticks;//获取当前时间到1年1月1日的总ticks数,ticks单位是100ns,即万分之一毫秒。
var dtbytes = BitConverter.GetBytes(dtvalue);// 将ticks时间戳转换为字节数组,默认是小端。
var bytes = new Byte[gid.Length + dtbytes.Length];// 实例化新的数字,用以存放时间值和GUID值。
// 因为BitConverter.GetBytes获得的Byte[]是小端,不符合排序要求,所以,要逆序写入bytes数组中,形成大端的方式。
// 将时间值放入bytes数组中。
for (long i = 0; i < dtbytes.Length; i++)
{
var cvalue = dtbytes[dtbytes.Length - i - 1];
bytes[i] = cvalue;
}
// 将guid的值,放入bytes数组中。
gid.CopyTo(bytes, dtbytes.Length);
// 将值转换为base64,主要原因是,前端、数据库比较容易处理字符串类型的数据。
var b64 = Convert.ToBase64String(bytes);
// 将无序的base64转换为有序的伪base64格式。
var ss = b64.ToArray();
for (var i = 0; i < ss.Length; i++)
{
ss[i] = dic[ss[i]];
}
return new string(ss);
}
/// <summary>
/// 仿base64的有序字典,其与base64相似,使用有限的字符,表示6bit的二进制,不足的地方补=。但是,与base64的区别是,字符串是按从小到大的次序表示000000到111111的数值的。
/// </summary>
public static readonly Dictionary<char, char> dic = new Dictionary<char, char>()
{
{'A','$'},{'B','-'},{'C','0'},{'D','1'},{'E','2'},{'F','3'},{'G','4'},{'H','5'},{'I','6'},{'J','7'},{'K','8'},
{'L','9'},{'M','A'},{'N','B'},{'O','C'},{'P','D'},{'Q','E'},{'R','F'},{'S','G'},{'T','H'},{'U','I'},{'V','J'},
{'W','K'},{'X','L'},{'Y','M'},{'Z','N'},{'a','O'},{'b','P'},{'c','Q'},{'d','R'},{'e','S'},{'f','T'},{'g','U'},
{'h','V'},{'i','W'},{'j','X'},{'k','Y'},{'l','Z'},{'m','a'},{'n','b'},{'o','c'},{'p','d'},{'q','e'},{'r','f'},
{'s','g'},{'t','h'},{'u','i'},{'v','j'},{'w','k'},{'x','l'},{'y','m'},{'z','n'},{'0','o'},{'1','p'},{'2','q'},
{'3','r'},{'4','s'},{'5','t'},{'6','u'},{'7','v'},{'8','w'},{'9','x'},{'+','y'},{'/','z'},{'=','!'}
};
}
internal class Program
{
static void Main(string[] args)
{
var preone = SeqGuid.NewGuid();
for(int i = 0; i < 9999999; i++)
{
var newone = SeqGuid.NewGuid();
if (String.CompareOrdinal(newone, preone)<0)//必须使用CompareOrdinal,因为Compare和CompareTo等都受本地的CultureInfo影响,可能会忽略大小写。
{
Console.WriteLine($"error ,{newone} < {preone}");
}
preone = newone;
}
Console.WriteLine("done...");
Console.ReadLine();
}
}运行结果:
执行1000万次,没有大小次序错误。单线程 的情况下,每秒生成143万个。
多线程并发测试
因为我的电脑只有20核,所以,使用15个线程来处理,为了避免受Task的优化影响,我们直接使用Thread来模拟。
static ConcurrentBag<string> exists = new ConcurrentBag<string>();
static void 测试并发唯一性()
{
Thread[] tks = new Thread[15];
for(var t = 0; t < 15; t++)
{
tks[t] = new Thread(workThread);
tks[t].Start();
}
Console.WriteLine("所有任务启动完成,等待执行完成中……");
for (var t = 0; t < 15; t++)
{
tks[t].Join();
}
Console.WriteLine($"全部执行完成,总生成guid个数:"+exists.Count);
}
static void workThread()
{
var count = 1000;
Console.WriteLine(Thread.CurrentThread.ManagedThreadId + ":启动");
for (int i = 0; i < count; i++)
{
var nid = SeqGuid.NewGuid();
if (exists.Contains(nid))
{
Console.WriteLine("出现重复guid:" + nid);
}
else
{
exists.Add(nid);
}
}
Console.WriteLine(Thread.CurrentThread.ManagedThreadId + ":完成");
}测试结果如下:

说明,借着.NET原本的GUID,完美的避开了并发情况下唯一的问题。至于说,高并发情况下次序问题,如果两个动作在100ns以内,是否区分次序或者不是那么重要了。
并且此GUID也并非是提供强一致次序(这种需求还是需要用Redis之类的来实现),而是提供有限的次序,以便解决数据库优化的问题。
转自:ensleep
链接:cnblogs.com/ensleep/p/17745166.html

