【翻译】JavaScript 中的函数式编程:函数、组合与柯里化
原文链接:https://blog.bitsrc.io/functional-programming-in-javascript-functions-composition-and-currying-3c765a50152e
豆皮粉儿,又见面啦!今天字节跳动数据平台的"阳羡"小哥哥给大家带来一篇翻译文章"JavaScript 中的函数式编程:函数、组合与柯里化",干货满满,不容错过!!!
本文作者:阳羡
面向对象编程[1]和函数式编程[2]是两种截然不同的编程范式,有各自的规则,也有各自的优缺点。
但是,JavaScript,并非一直使用一种编程范式,而是兼具两者的特征。给你提供了普通 OOP 语言一些方面的能力,比如类、对象、继承等。但同时,它也给你提供了一些函数式概念,比如高阶函数,也提供了组合与柯里化的能力。
高阶函数
先说说我在本文中涉及的三个概念中最重要的一个:高阶函数。
拥有对高阶函数的访问权意味着函数不仅仅是一个你可以从代码中定义和调用的构造,事实上,你可以将它们作为可赋值的变量,即函数是一等公民。
如果你写过一些 JavaScript 的话,这一点应该不会让人感到惊讶,毕竟,你应该已经能够简单地从网上按照例子将匿名函数赋值给变量了。将函数赋值给变量在日常使用中并不罕见。

如果 JavaScript 是你用来学习编程的第一门语言,那么你可能会对上述逻辑在许多其他语言中是无效的而感到惊讶。像赋值一个整数一样赋值一个函数其实非常有用,事实上,本文所涉及的大部分主题都是由此衍生而来。
高阶函数的优势:封装行为
通过高阶函数,我们不仅可以像上面一样给变量赋值函数,而且,我们还可以在函数调用时将其作为参数传递。这又为创建动态逻辑打开了大门,你可以通过直接将复杂的行为作为参数传递来重用逻辑。
想象一下,在一个纯粹的面向对象的环境中工作,你需要重用一个逻辑,你知道一个基本逻辑可以被扩展并作为复杂逻辑的一部分。在这种情况下,你可能会选择使用继承,通过将该逻辑封装在一个抽象类中,然后将其扩展为一组派生类,这些类利用该通用逻辑并对其进行补充。这是完美而高效的 OOP 准则,但让我们看看我们刚才做了什么。我们:
创建了一个抽象的结构来封装我们的可重用逻辑。
创建了一个二级的派生类
让后者在前者的基础上进行逻辑扩展。
但是,在函数式的环境下,为了复用逻辑,我们可以简单地将需要复用的逻辑提取到一个函数中,然后将这个函数作为参数传递给任何其他可以从这种封装行为中受益的函数。我们只是在创建函数,而不是创建“模版”。
下面的例子试图展示我上面解释的内容。第一段代码展示了你如何在 OOP 环境中去重用一个格式化并输出的逻辑。

然而,第二个例子表明,通过将逻辑提取出来,并使用函数封装,你可以用很少的成本来创建你所需要的逻辑。你可以继续添加更多的格式化( format)和输出(output)函数,然后只需用一行代码将它们组合在一起就可以了。
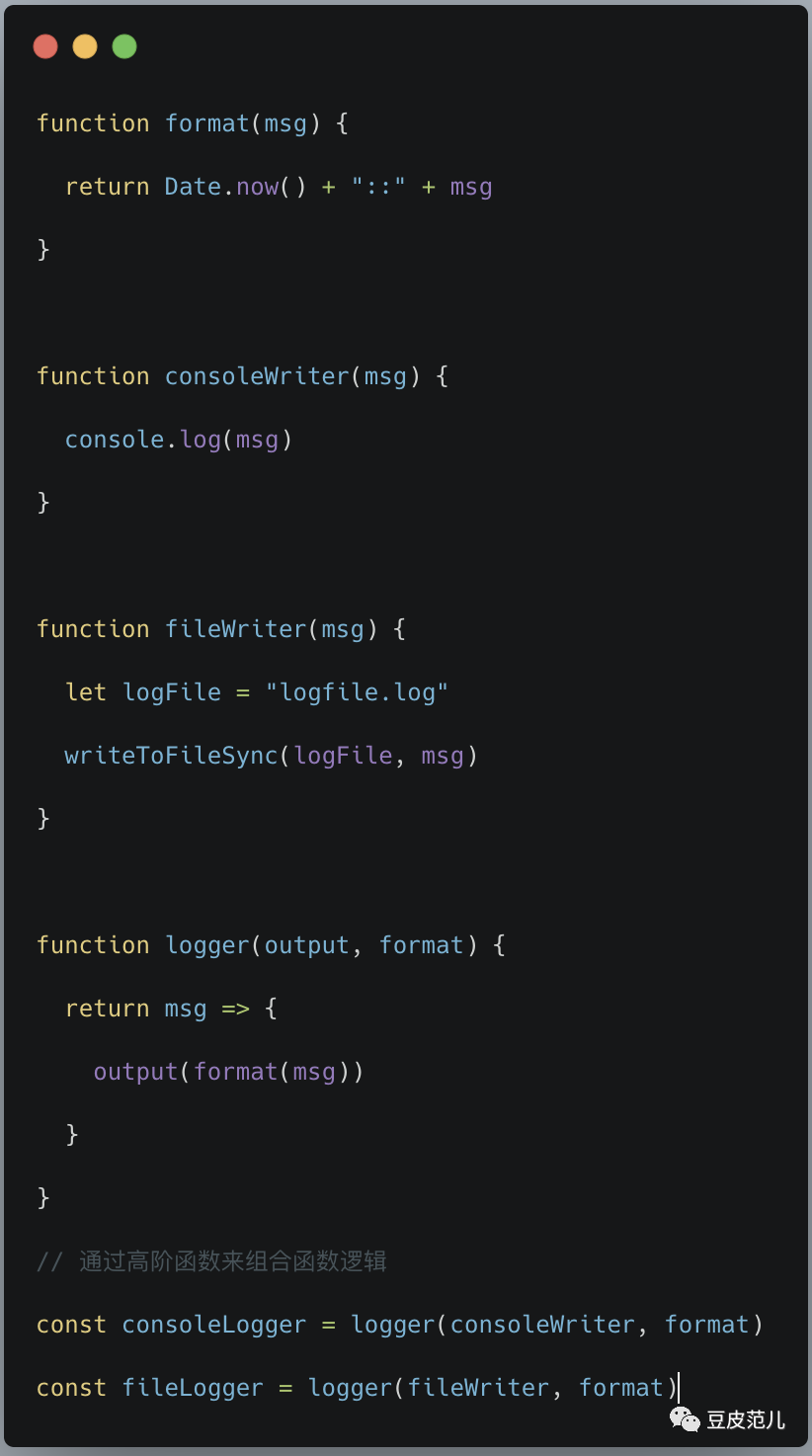
我的意思是,这两种方法都有优点,而且都是非常高效的,没有高低优劣之分。函数式有多么令人难以置信的灵活性,以及我们如何使用基本的函数式原理,这仅仅是因为我们有能力将行为(即函数)作为参数传递,就好像它们是一个基本类型,如整数或字符串。
高阶函数的优势:整洁代码
整洁代码的最好例子就是数组方法,如 forEach ,map ,reduce 等。在非函数式语言中,例如 C 语言,迭代一个数组的元素,并对它们进行转换,需要使用 for 循环或其他循环结构。它们要求你以一种非常命令式的方式编写代码(换句话说,你需要表达事情如何在循环内发生),而函数式则允许更多的声明式编程风格(你最终指定需要发生什么)。

你的代码实际上是在说:
声明一个新的变量 i 作为 myArray 的索引 它的值范围从 0 到 myArray 的数组长度。
遍历i的值,然后把 i 位置的 myArray 的值乘 2,并将其添加到 transformedArray 数组中。
它当然是可行的,而且比较容易理解,但是,逻辑的复杂度会迅速升级,并且阅读逻辑所需的认知成本也会增加。然而,表达同样的逻辑,函数式可能更具有可读性:

本质上,这段代码是说
用 double 函数映射 (map) myArray 的元素,并将结果赋值给 transformedArray。
因为逻辑被隐藏在两个函数(map和double)中,所以你不必担心理解它们的工作原理。你也可以在第一个例子中把乘法逻辑隐藏在一个函数里面,但是仍然需要暴露迭代逻辑,晦涩的迭代逻辑是你作为一个阅读代码的人,必须在头脑中解析以理解其工作原理的重要部分。
柯里化(currying)
函数柯里化是指将一个多参数的函数变成一个少参数的函数,并将部分参数固定下来的编程思想。让我用一个例子来解释。

现在,如果你想做的是将 10 加到一系列值上,你可以调用 add10,而不是每次都用相同的第二个参数调用 adder。我知道这可能是一个简单的例子,当你寻找柯里化时,可能到处都是这个例子,但考虑到你正在做的事情:你正在利用 adder 函数的逻辑,并创建该函数的专门版本,换句话说,你正在扩展该函数,就像你使用一个类一样。
你可以把柯里化看作是函数式编程的继承,按照这个思路,再回到上面格式化输出的例子,你可以这样编写你的代码:
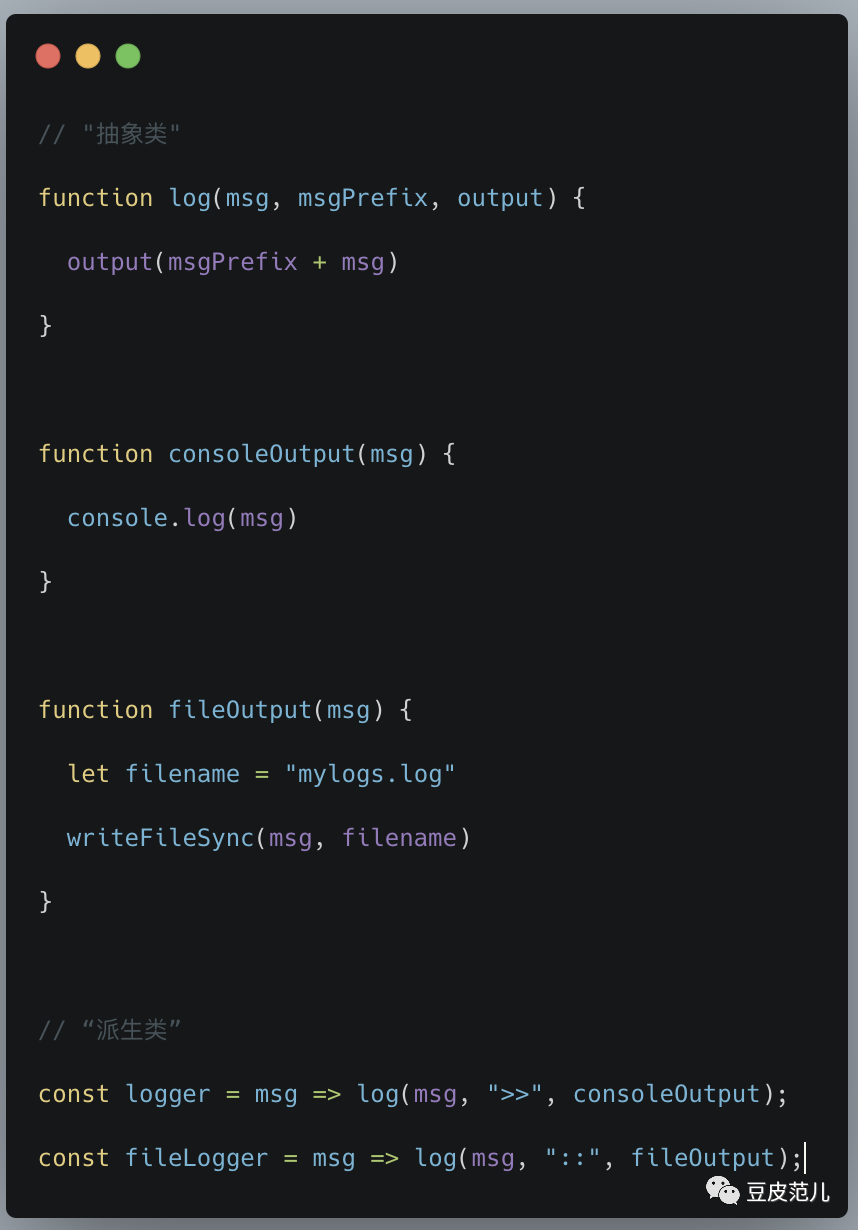
本质上,你有一个叫做 log 的函数,它需要三个参数,而我们把它柯里化成专门的版本,只需要一个,因为另外两个已经被我们选好了。
需要注意的是,我把 log 函数当作一个抽象类,只是因为在我的例子中,你不会想直接使用它,然而这样做没有任何限制,因为这只是一个普通的函数。如果我们使用的是抽象类,你就不能直接实例化它。
组合(Composition)
最后,函数组合是高阶函数的另一个非常有趣的衍生品。乍一看,人们很容易把组成混淆为柯里化的情况,或者也许反过来说,有柯里化的函数而不是直接的值(就像我们在上面的记录仪例子中做的那样)可以被认为是函数组合。
这些观点其实都没有错,当你开始使用函数式时,这两个概念之间有一条非常细微的界限。具体来说,组成的定义如下:
在计算机科学[3]中,函数组合是一种将简单的函数[4]组合起来建立更复杂的函数的行为或机制。与数学[5]中通常的函数组合[6]一样,每个函数的结果作为下一个函数的参数传递,最后一个函数的结果就是整个函数的结果。
这是维基百科上关于函数组成的定义,最后加粗的部分是我强调的,因为那是关键部分。在柯里化中,你没有这个限制,你可以很容易地使用预先设定的函数参数,如果它们是函数,它们不必一个接一个地调用,让第一个函数的结果成为第二个函数的输入,以此类推。
与柯里化不同,这是一个强大的工具,因为在这里,只有部分功能,每个功能都在完成一个特定的任务,等待着被组成更大更复杂的东西。想想看,就好像函数是乐高积木一样,通过组合,只要你把正确的逻辑柯里化,并以正确的顺序组合在一起(即只要你以正确的顺序组合成正确的函数),你就能创造出任何你能想到的东西。
如果你以前使用过 Linux 发行版,你可能已经注意到,Linux 中的 CLI 工具遵循一个非常确定的模式:它们只做一件事,并且能够从标准输入中读取结果,并将其输出到标准输出。因此,允许用户将多个命令组合成一句功能强大的命令,例如:
$ cat myfile.txt | wc -l
如上所示,我是在读取一个文件,并计算它的行数,然而,如果以不同的方式或与其他命令组合,输出可能会有很大的不同。同样的情况也发生在函数上,如果你在设计函数的时候,让一个函数的输出可以成为另一个函数的输入,你也可以像这样组合它们。

看看上面和最后的例子,我创建了四个不同的处理字符串的函数,并将它们组合成三个不同的函数。你可以通过组合函数来创建新函数。这就是组合的魅力所在。
仔细看一下代码,有几处值得关注。
有些函数(replace和findMatches)实际上是接受参数并返回一个函数。这是为了使它们更通用,由于JS将返回的函数的上下文与函数本身一起保存(即闭包),我们能够将这些参数作为被返回函数的 "全局 "变量,并作为组合的一部分使用。
请注意 compose 函数,它是利用 ES6 的结构操作符,简单地在函数参数上进行迭代,并执行它们,然后将其结果发送给下一个函数。reduceRight 的使用保证了我们在函数列表中从右到左进行执行,这就是为什么我总是把小写字母加到最后一个。如果你想让顺序反过来,你可以直接使用 reduce 来代替。
结论
如果使用得当,高阶函数以及柯里化和组合都是非常强大的工具。我知道,如果你不习惯于使用函数式的思维模式,而是更愿意使用类和对象,这些技术可能看起来有悖于直觉,但它们本质上并不晦涩难懂,只是需要换个角度去思考。
感受并享受 JavaScript 的函数式编程吧!
你之前使用过这些工具吗?你更喜欢用函数式编程思想写代码吗?还是你更喜欢 OOP 开发?欢迎在评论区发表你的看法。
感谢阅读,我们下期再见!
References
[1] 面向对象编程: https://en.wikipedia.org/wiki/Object-oriented_programming
[2] 函数式编程: https://en.wikipedia.org/wiki/Functional_programming
[3] 计算机科学: https://en.wikipedia.org/wiki/Computer_science
[4] 函数: https://en.wikipedia.org/wiki/Subroutine
[5] 数学: https://en.wikipedia.org/wiki/Mathematics
[6] 函数组合: https://en.wikipedia.org/wiki/Function_composition
