LeetCode刷题实战391：完美矩形-技术圈

算法的重要性，我就不多说了吧，想去大厂，就必须要经过基础知识和业务逻辑面试+算法面试。所以，为了提高大家的算法能力，这个公众号后续每天带大家做一道算法题，题目就从LeetCode上面选！

今天和大家聊的问题叫做 完美矩形，我们先来看题面：

https://leetcode-cn.com/problems/perfect-rectangle/

Given an array rectangles where rectangles[i] = [xi, yi, ai, bi] represents an axis-aligned rectangle. The bottom-left point of the rectangle is (xi, yi) and the top-right point of it is (ai, bi).

Return true if all the rectangles together form an exact cover of a rectangular region.

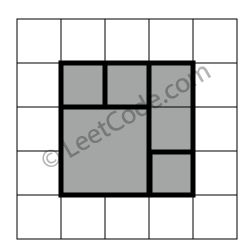
我们有 N 个与坐标轴对齐的矩形, 其中 N > 0, 判断它们是否能精确地覆盖一个矩形区域。

每个矩形用左下角的点和右上角的点的坐标来表示。例如，一个单位正方形可以表示为 [1,1,2,2]。( 左下角的点的坐标为 (1, 1) 以及右上角的点的坐标为 (2, 2) )。

示例

示例 1:
rectangles = [
  [1,1,3,3],
  [3,1,4,2],
  [3,2,4,4],
  [1,3,2,4],
  [2,3,3,4]
]
返回 true。5个矩形一起可以精确地覆盖一个矩形区域。

示例 2:
rectangles = [
  [1,1,2,3],
  [1,3,2,4],
  [3,1,4,2],
  [3,2,4,4]
]
返回 false。两个矩形之间有间隔，无法覆盖成一个矩形。

示例 3:
rectangles = [
  [1,1,3,3],
  [3,1,4,2],
  [1,3,2,4],
  [3,2,4,4]
]
返回 false。图形顶端留有间隔，无法覆盖成一个矩形。

示例 4:
rectangles = [
  [1,1,3,3],
  [3,1,4,2],
  [1,3,2,4],
  [2,2,4,4]
]

返回 false。因为中间有相交区域，虽然形成了矩形，但不是精确覆盖。

解题

https://blog.csdn.net/Forlogen/article/details/109827717

何谓完美矩形？根据题目的描述可知，给定的所有小矩形如能构成完美矩形，需满足如下的条件：

所有小矩形构成的图形仍然是一个矩形

构成的矩形不能有重叠和空缺部分

以题目给定的第一个例子进行说明，给定小矩形的情况如下所示：

如上图所示，给定的5个小矩形刚好组成一个大的矩形，大矩形的左下角和右上角坐标分别是[1,1]和[4,4]。矩形之间没有重叠部分，大矩形中间也没有空缺。再去看其他例子，应该就能明白为什么不能构成完美矩形了。

那么如何判断给定的例子满足要求呢？对于一个单独的矩形来说，它包含点和面积两大要素。如果要构成完美矩形，首先，所有小矩形相加的面积之和要等于完美矩形的面积。而想要知道完美矩形的面积，又必须首先知道它的左下角[X1,Y1]和右上角坐标[X2,Y2]。而[X1,Y1]就是所有小矩形坐标中最靠左下角的那个，[X2,Y2]是所有小矩形坐标最靠右上角的那个。知道了[X1,Y1]和[X2,Y2]，必然可以计算出完美矩形的面积，只有小矩形的面积之和等于完美矩形的面积，对应的结果才可能为true。

但是面积相等只能说有希望构成完美矩形，并可能一锤定音。如下所示，所有的小矩形构成了一个大矩形，虽然有一个单位的空缺，但恰好有一个单位的重叠。因此，如果单纯从面积相等判断好像是可行的，但显然是无法满足要求的。

因此，我们还需要从点的角度进行进一步判断。下面给出一个合法的例子如左图所示，不合法的例子如右图所示，同时用数字标记了所有小矩形包包含的顶点出现的次数。可以发现，合法的例子中，出现次数为1的顶点就是最后完美矩形的四个顶点，其他的顶点都出现了两次。而不合法的例子中，出现次数为1的顶点不只是完美矩形的四个顶点。

因此，我们可以在遍历小矩形的同时记录顶点出现的情况。如果当前顶点没有遍历过，则将其加入到集合中，否则将其从集合中删除。如果最后集合中只包含可能的完美矩形的四个顶点，那么说明例子是合法的，否则说明无法构成完美矩形。

总结，如果解该题需要遍历所有的小矩形，遍历过程中需要等到完美矩形的左下角和右上角坐标、矩形面积之和，以及顶点的出现情况，最后，判断小矩形面积之和和完美矩形面积之和是否相等，集合中是否只包含4个顶点且是完美矩形的四个顶点，只有这两个条件同时满足才能构成完美矩形。

解码代码如下所示：

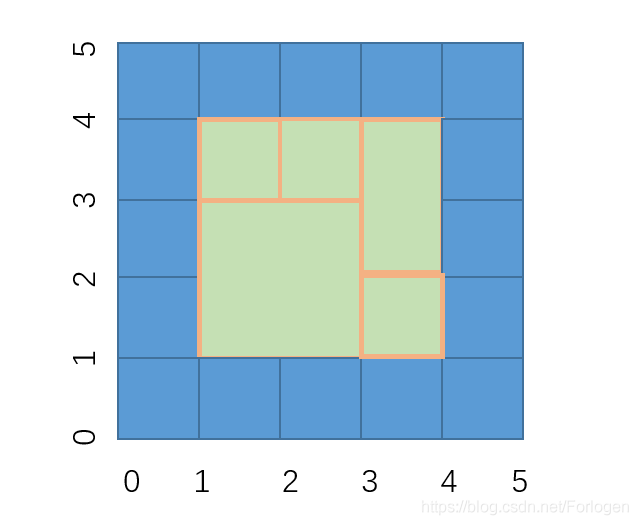
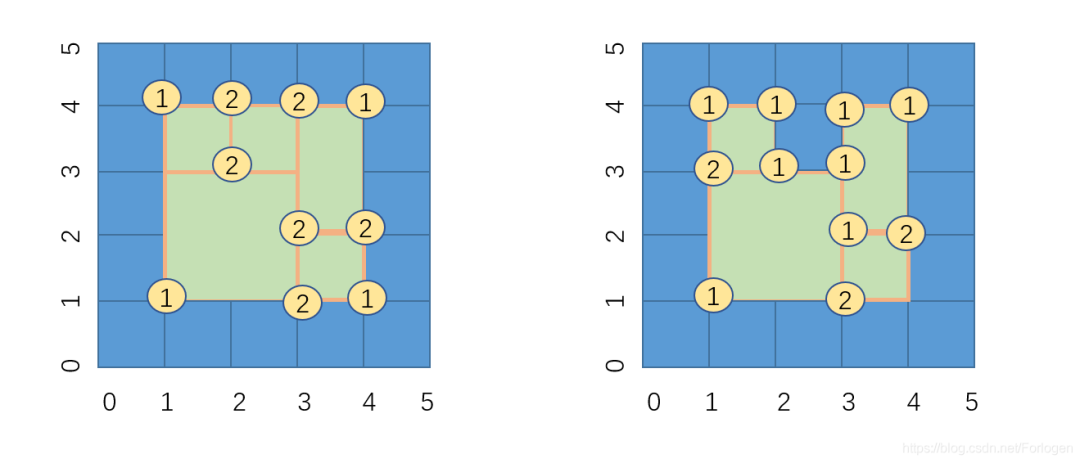
class Solution {
    public boolean isRectangleCover(int[][] rectangles) {
        // 完美矩形的左下角和右上角坐标
        int X1 = Integer.MAX_VALUE, Y1 = Integer.MAX_VALUE;
        int X2 = Integer.MIN_VALUE, Y2 = Integer.MIN_VALUE;
    
        // 小矩形面积之和
        int areas = 0;
        // 记录所有顶点的出现情况
        Set<String> points = new HashSet<>();
        for (int[] rectangle : rectangles) {
            int x1 = rectangle[0], y1 = rectangle[1], x2 = rectangle[2], y2 = rectangle[3];
            // 更新坐标
            X1 = Math.min(x1, X1);
            Y1 = Math.min(y1, Y1);
            X2 = Math.max(x2, X2);
            Y2 = Math.max(y2, Y2);

            areas += (x2 - x1) * (y2 - y1);
            // 判断顶点是否出现过
            String[] ps = {x1 + " " + y1, x2 + " " + y2, x1 + " " + y2, x2 + " " + y1};
            for (String s : ps) {
                // 没有出现过，添加；否则，移除
                if(points.contains(s)){
                    points.remove(s);
                } else {
                    points.add(s);
                }
            }
        }
    
        // 面积是否相等 
        int expected = (X2 - X1) * (Y2 -Y1);
        if(areas != expected){
            return false;
        }
        // 顶点情况是否满足
        if(points.size() != 4 || !points.contains(X1 + " " + Y1) || !points.contains(X2 + " " + Y2) || !points.contains(X1 + " " + Y2) || !points.contains(X2 + " " + Y1)){
            return false;
        }
        return true;
    }
}