打破你的认知，Java除以0一定会崩溃吗？

在这个浮躁的社会，我们都学会了一种技能，快速学习使用各种开源库、开源框架。

学习使用各种高端大气的技术，热修复、插件化、模块化、ORM……

这些技能固然重要，但是有时候也要放慢脚步，耐着性子，打打基本功。

不要看不起这些零零碎碎的基础知识，这些基础日积月累，慢慢的会让你跟同事拉开差距。

接下来，我们直奔主题。开始我们的基本功。

System.out.println("1/0=" + 1/0);

大叔的灵魂拷问：

运行直接崩溃。

我们再来看一行代码：

System.out.println("1.0/0=" + 1.0/0);

大叔的灵魂拷问：

会崩溃吗？如果不会，会输出什么呢？

输出日志：

为什么浮点数除以0不会崩溃？

我们先说结论：

因为java的float和double使用了IEEE 754标准。

这个标准规定：浮点数除以0等于正无穷或负无穷。

4.1、Double类的定义

于是我们打开Double这个类来看看。

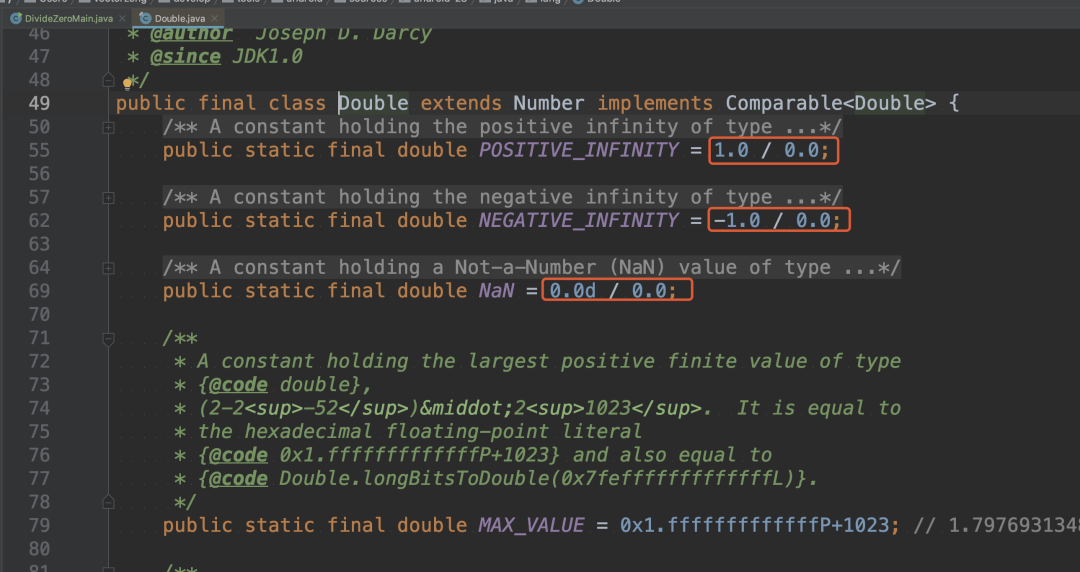
infinity单词的意思是：无穷大

NaN是Not a Number的简称，也就是非数。

于是，我们发现，正无穷大的定义居然是1.0f/0.0f 。负无穷大的定义为-1.0f/0.0f，非数的定义为0.0f/0.0f

4.2、代码段3

我继续看一个代码段：

public static void main(String[] args) {
  System.out.println("1.0/0=" + 1.0/0);
  System.out.println("-1.0/0=" + -1.0/0);
  double positiveInfinity = 1.0/0;
  double negativeInfinity = -1.0/0;
  System.out.println("(positiveInfinity==negativeInfinity)=" + (positiveInfinity==negativeInfinity));
  System.out.println();

  System.out.println("100.0/0=" + 100.0/0);
  System.out.println("-100.0/0=" + -100.0/0);
  System.out.println();

  System.out.println("0.0/0=" + 0.0/0);
  System.out.println("(-0.0==0.0)=" + (-0.0==0.0));
}

大叔的灵魂拷问：

上面的代码段会输出什么呢？

运行结果：

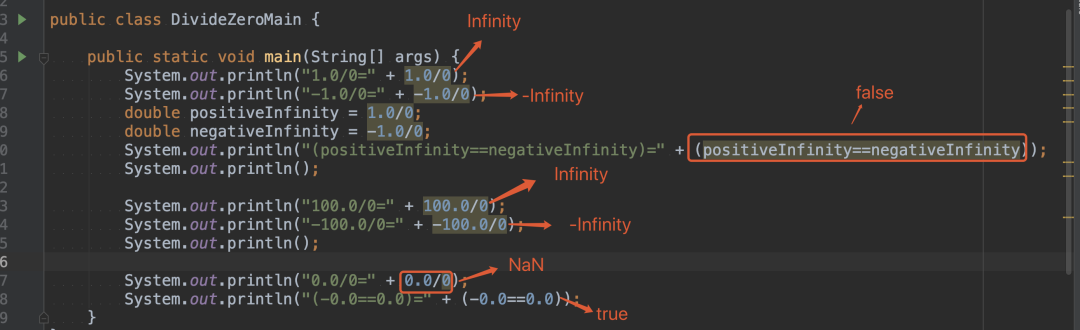
4.3 接着，我们来看看，java语言规范（ Java Language Specification）

https://docs.oracle.com/javase/specs/jls/se7/html/jls-4.html#jls-4.2.3

注意关键词1：

IEEE 754

java的单精浮点数float和双精浮点数double，符合IEEE 754标准。

搜索公众号程序员小乐回复关键字“offer”，获取算法面试题和答案。

IEEE 754：二进制浮点数算术标准 ，这个标准描述了浮点数的存储以及处理的一些规范。

关于IEEE754，百度百科

https://baike.baidu.com/item/IEEE%20754/3869922?fromtitle=IEEE754%E6%A0%87%E5%87%86

IEEE-754 references

https://web.archive.org/web/20070505021348/http://babbage.cs.qc.edu/courses/cs341/IEEE-754references.html

注意关键词2

A NaN value is used to represent the result of certain invalid operations such as dividing zero by zero.

翻译过来的就是：NaN = 0.0/0.0

这也就是我们看到Double类里面NaN的定义。

我们把这个文档往下翻一些，会发现这么一句：

for example, 1.0/0.0 has the value positive infinity, while the value of 1.0/-0.0 is negative infinity.

翻译成中文：1.0/0.0 等于正无穷大,1.0/-0.0 等于负无穷大

于是我们明白，浮点数除以0并不会崩溃，是符合IEEE 754规范。

也正是因为 IEEE 754的规范就是这么规定的，所以java才这么实现的。

下面这段来自，维基百科，https://en.wikipedia.org/wiki/Division_by_zero

我们即使知道了，浮点数除以0不会崩溃，知道了IEEE标准，有什么用呢？

很多人都会觉得，费这么大劲，理解了，浮点数除以0不会崩溃，能有什么用呢？平时我们写代码都不会除以0。这么骚的操作，我才不会这么干。

是的，这个操作是有点骚，你不会这么干并不代表其他同事不会这么做。而且很可能你这么干了自己不知道。

在我们写业务代码的时候，这个知识点，很少很少能用上。

但是当我们刚好遇到除以0导致的bug的时候，这个时候就非常有用。

尤其像android的app，用户在线上遇到的bug，我们无法复现，只能通过日志去分析排查时；

这个时候每个程序员都是福尔摩斯，根据一行行日志线索，配合实际代码，排查问题的可能性。

如果我们的认知是错误的，任何数除以0都会崩溃，那么我们的分析将会直接绕过真相去推理。于是得出结论，怎么可能有bug，不可能的。

于是浪费了很多时间，去收集线索，去推翻我们固有的认知，才能找到真相。

假如我们一开始就有正确的常识，我们就会少走很多弯路。

大叔给大家，讲一个工作中真实的故事：

有位同事写了这么一段代码

/**
* 速度换算 米/秒
* @param distance 距离，单位米
* @param time 时间，单位秒
*/
float computeSpeed(float distance, long time){
  return distance/time;
}

然后有一天突然某同事从另一个进程获取到数据传入这个函数。

再然后，突然有一天发现，速度显示一串很奇怪的数字。

于是……接下来的故事，便如你们所想。

原本1小时就解决的bug，花了5个小时。

也正如，blog开头的引言所表达的。不要小看这些零零碎碎的知识点。

参考资料：

https://juejin.im/post/5edcc957e51d4578801683c0

关于IEEE754，百度百科

IEEE-754 references

https://stackoverflow.com/questions/12954193/why-does-division-by-zero-with-floating-point-or-double-precision-numbers-not