SPC8大判异规则的概率计算 和如何自定义SPC判异规则让SPC控制图...

我们在做质量异常判定的时候，最常用的就是SPC控制图（如果还用minitab手工做SPC控制图就out了）。那么我们最多接触的就是SPC控制图的8大判异规则，这个8大判异规则是来自统计学中的正态分布而得到的一个判断小概率事件是否发生的依据。

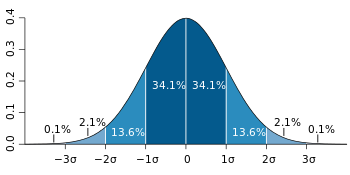
但我们有时候又需要一些更敏感的判异规则，并且也要知道这些更敏感的判异规则和标准规则有多大的差异（事件发生的概率差异），并且通过什么系统或者怎么样的计算方法才能实现这些更敏感的SPC判异规则。

这篇文章全面介绍了标准SPC判异规则的事件发生的概率的计算、自定义判异规则以及事件发生的概率的计算，最后简单介绍如何在系统中实现。

第一部分 SPC异常事件的概率计算

我们先介绍一下SPC的判异规则的原理和算法依据。首先我们基于样本总体满足正态分布的前提下做的SPC分析，下图我们列举正态分布的每一个标准差的概率值，方便我们对SPC的判异规则的事件发生概率进行计算。

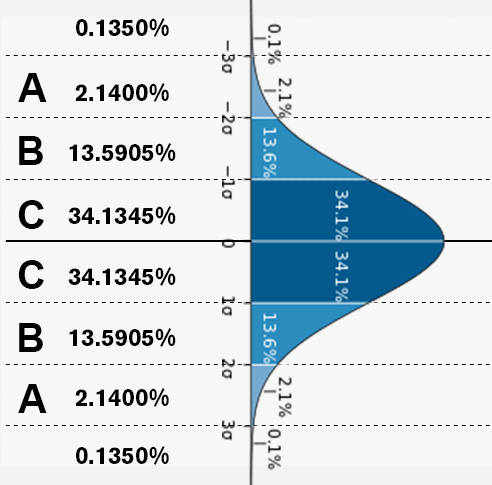
比如一个点远离3倍标准差（C区之外），可以看到上面的0.1350%的概率，因为有两个方向，所以一个点远离3倍标准差（C区之外）的事件概率就是0.1350%*2=0.27%

有比如连续9个点在同一侧，

A+B+C = 34.1345%+13.5905%+2.1400% = 49.865%，

那么在上方连续9个点的发生的概率就是 ：

49.865^9 = 0.1906%，

下方发生的概率一样，所以连续9个点在同一侧的概率是

0.1906%*2 = 0.3812%

上图的数据作为下面详细介绍SPC标准判异规则的计算方法的依据。

第二部分  SPC标准判异规则

我们先详细看看这8个判异规则的。然后再看看其他更敏感的判异方法。

1）一个点远离中心线超过3倍标准差

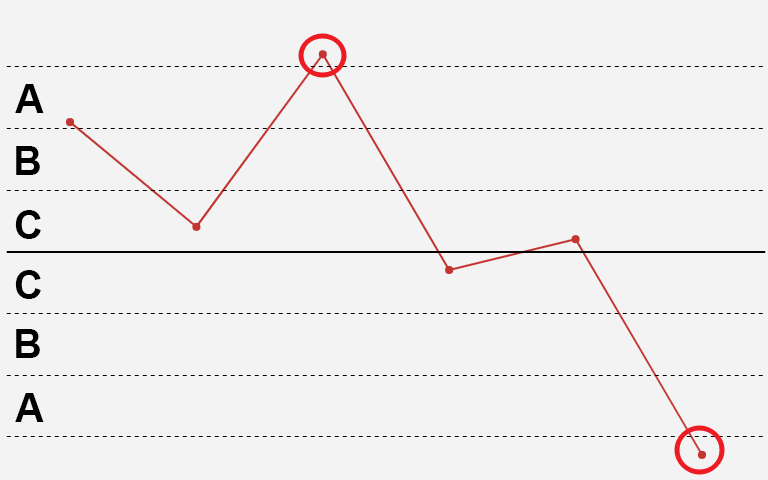
解释：正态分布中出现在C区以外的概率是0.27%，基本上认为是小概率事件，如果事件发生了，一定是特殊原因导致！

原因：一般认为是新员工，工艺方法错误，机器故障，原材料不合格，测量错误，计算错误，检验方法或标准变化。

2）连续9个点在同一侧

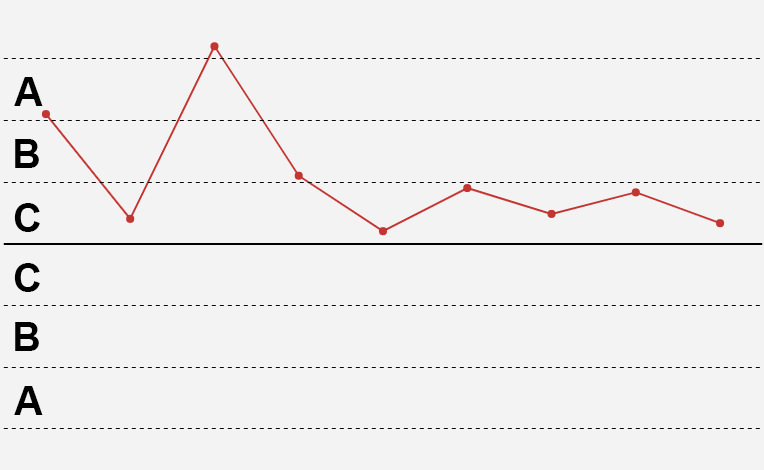
解释：此准则作为准则一而补充的，以提高控制图的灵敏度，选择9点是为了使其犯第一种错误的概率α与准则一的0.27%大体相仿。

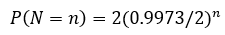
连续9个点在同一侧事件发生的概率为：

P(N=9) = 2*（0.9973/2）^9 = 0.38%

原因：均值可能发生了便宜，一般认为是新员工，工艺方法错误，机器故障，原材料不合格，测量错误，计算错误，检验方法或标准变化。

3）连续6个点持续上升或下降

解释：此条准则针对过程平均值的倾向性而设计的，它判定过程平均值的较小倾向要比准则一更为灵敏。其产生原因可能是工具损坏，或作业员技能改进等。

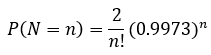
连续6个点持续上升或下降事件发生的概率为：

P(N=6) = (2/6!)*(0.9973)^6= 0.27%

原因：它可以判定过程平均值较小的趋势变化，可能刀具模具等工具的磨损，维护保养水平降低，操作工的技能越来越熟练。

4）14个点交互升降

解释：出现这种现象是由于轮流使用两台设备或两位操作人员轮流操作而引起的系统效应。实际上这是一个数据分层不够的问题，选择14点是通过统计模拟试验而得出的.

14个点交互升降事件发生的概率为：0.4%

原因：轮流使用两台设备或两个操作工操作，分别针对两个模穴定期抽样但一起统计等导致数据分层不够。

5）连续3点中有2点落在中心线同一侧的B区以外（2标准差和3标准差之间）

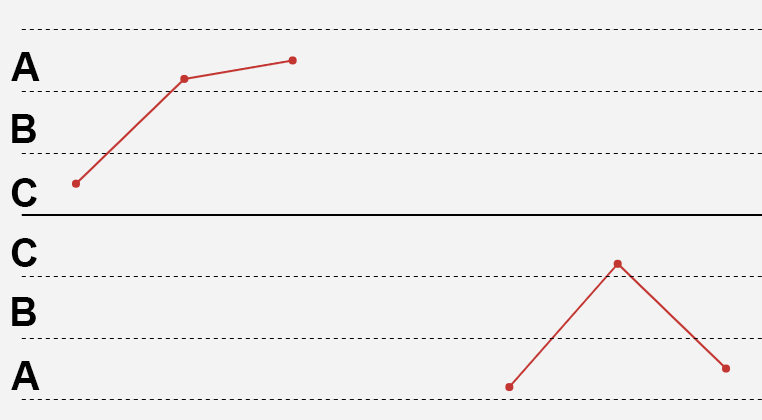
解释：过程平均值的变化通常可由本准则判定，它对于变异的增加也较灵敏。

正态分布中位于均值的一侧，在均值＋2σ和均值＋3σ之间的概率是 (0.9973-0.9545)/2=0.0214。

如果三个点中有两个点出现在这个区间的概率是0.0214平方乘以另外一个点子出现的概率，而另一个点子可以出现在除中心线一侧A区以外的任一个地方。所以另一个点子出现的概率是（0.9973－0.0214）。

另外这三个点中的两个点可以是第一第二点，也可以是第一第三点还可以是第二第三点，也就是一共有种方式。还有A区在中心线的两侧都有。

连续3点中有2点落在中心线同一侧的B区以外，事件发生概率就是：

P = 2*3*0.0214^2*(0.9772-0.0214) = 0.26%

原因：可能标准差已经变大。一般认为是新员工，工艺方法错误，机器故障，原材料不合格，测量错误，计算错误，检验方法或标准变化。

6）连续5点中有4点落在中心线同一侧C区以外（远离一倍标准差）

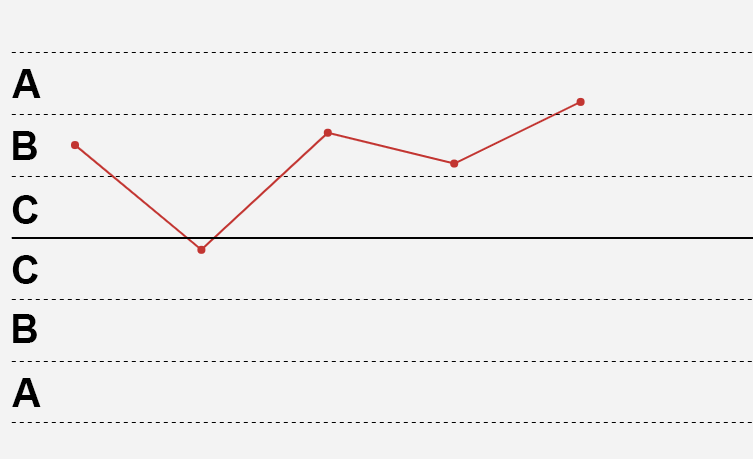
解释：此准则与上一准则类似，这第5点可在任何地方。本准则对于过程平均值的偏移也灵敏。参考准则4的思路，

连续5点中有4点落在中心线同一侧C区以外，事件发生的概率为：

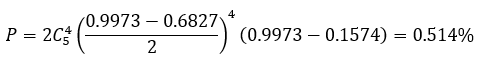
原因：可能均值发生了变化，一般认为是新员工，工艺方法错误，机器故障，原材料不合格，测量错误，计算错误，检验方法或标准变化。

7）连续15点落在中心线两侧的C区内

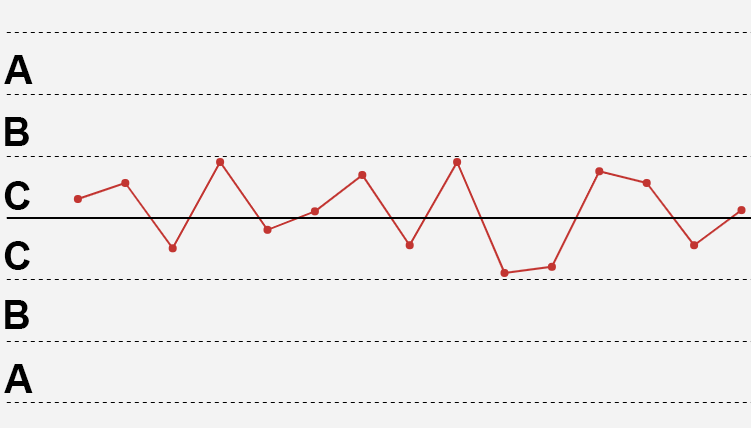
解释：对于本准则的现象，不要被它良好现象所迷惑，而应注意它的非随机性。连续15点在中心线在1倍标准差之内事件发生的概率为：

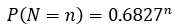
P(N=15)= 0.326%

原因：造成这种现象的原因有2种：数据虚假或数据分层不够。

8）连续8点落在中心线两侧且无一在C区内（1倍标准差之外）

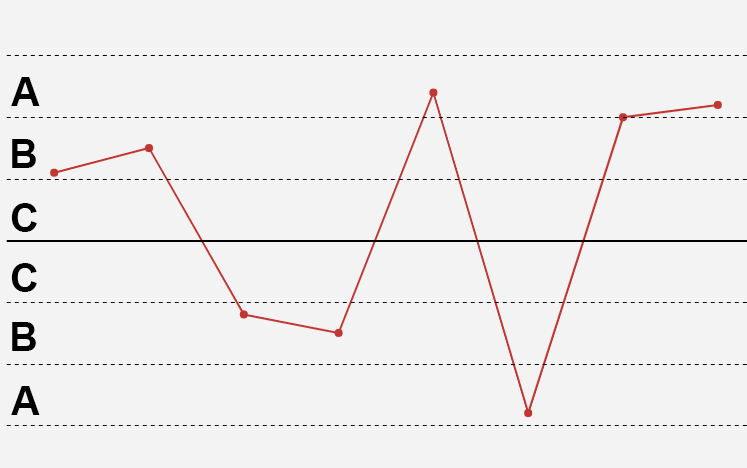
解释：一个点落在A、B两区内的概率是0.1573×2＝0.3146，连续n个点落在A、B两区内的概率应该是0.3146的n次方，连续n点落在中心线两侧且无一在C区内的事件发生的概率为：

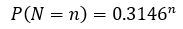
连续8点落在中心线两侧且无一在C区内的事件发生的概率为:

P(N=4) =(0.3146)^8=0.98%

P(N=5) =(0.3146)^8=0.31%

P(N=6) =(0.3146)^8=0.09%

P(N=7) =(0.3146)^8=0.03%

P(N=8) =(0.3146)^8=0.01%

从上面的概率来看，似乎应该是“连续5点落在中心线两侧且无一在C区内”作为判异准则更合适些，和其他几个判异标准比较接近。

原因：数据分层不够(SPC没有分模穴去分开做，没有分班次去做等等)

第三部分 自定义SPC判异规则

如果我们想提高异常判定的敏感度，该如何做呢？

9）连续N个点在同一侧

我们可以通过调整这个N来调整我们对异常判定的敏感度。下面是N个点在同一侧的事件发生的概率，如果要判异规则敏感一点，那么我们可以选择N=5、6、7、8这些数。

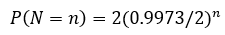
P（N=7）= 1.53%

P（N=8）= 0.0076%

P（N=9）= 0.38%（标准SPC判异规则）

P（N=10）= 0.19%

10）连续N个点持续上升或下降

我们可以通过调整这个N来调整我们对异常判定的敏感度。下面是N个点持续上升或下降事件发生的概率，如果要判异规则敏感一点，那么我们可以选择N=4、5 这些数。

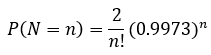
P（N=4）=1.644%

P（N=5）=1.644%

P（N=6）= 0.273%（标准SPC判异规则）

11）连续N点落在中心线两侧的C区内

我们可以通过调整这个N来调整我们对异常判定的敏感度。下面是N个点落在中心线两侧的C区内事件发生的概率，如果要判异规则敏感一点，那么我们可以选择N=12、13 这些数。

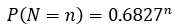
P(N=12) = 1.03%

P(N=13) = 0.70%

P(N=14) = 0.48%

P(N=15) = 0.33%（标准SPC判异规则）

P(N=16) = 0.22%

12）连续N点落在中心线两侧且无一在C区内（1倍标准差之外）

连续n点落在中心线两侧且无一在C区内的事件发生的概率为：

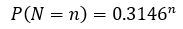
我们可以通过调整这个N来调整我们对异常判定的敏感度。下面是连续N点落在中心线两侧且无一在C区内事件发生的概率，如果要判异规则敏感一点，那么我们可以选择N=4、5 这些数。

P(N=4) =(0.3146)^8=0.98%

P(N=5) =(0.3146)^8=0.31%

P(N=6) =(0.3146)^8=0.09%

P(N=7) =(0.3146)^8=0.03%

P(N=8) =(0.3146)^8=0.01%（标准SPC判异规则）

第四部分 自定义SPC判异规则的系统实现

首先标准的SPC判异规则是必须支持的，对于上文提到的四个自定义判异规则，每一个规则都可以选择适合自己的N来提高SPC判异的敏感度，并且SPC能实时自动监控，无需手动导出导入数据来做SPC分析。

这些功能在一个叫简易SPC的简单的SPC产品中就实现了。具体请看他们的demo：

http://www.simplespc.cn/demos