Go 内存页管理 与 radix tree
Go语言最初采用了TCmalloc算法作为其内存分配的指导思想,TCmalloc算法的核心想法之一是将内存分成若干大小级别的class块。这种算法由于需要将对象的内存映射到最接近的class,因此会有内存浪费的问题。但是分成的若干级别可以free-lock 进行访问,这在多线程的程序中,性能会大大提升。
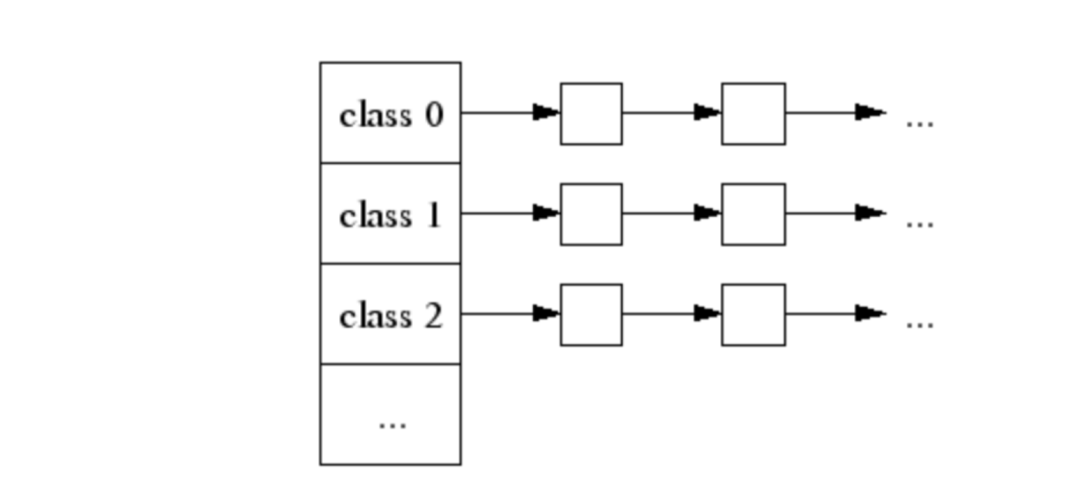
世面上Go语言的文章在介绍内存分配时,比较强调在mallocgc函数中,如何根据对象大小放入到不同的span class中。存储在不同P中的不同级别的span块,以及span中对象的cache,能够帮助非常快的分配对象。它能够说明有了span之后快速分配的问题,但是不能解决span是如何来的问题。span怎么来就涉及到Go语言对于内存页(page 8KB)的管理。
在Go1.12的时候,Go语言采用了Treap 进行内存的管理,Treap 是一种引入了随机数的二叉树搜索树,其实现简单,并且引入的随机数以及必要时的旋转保证了比较好的平衡特性。
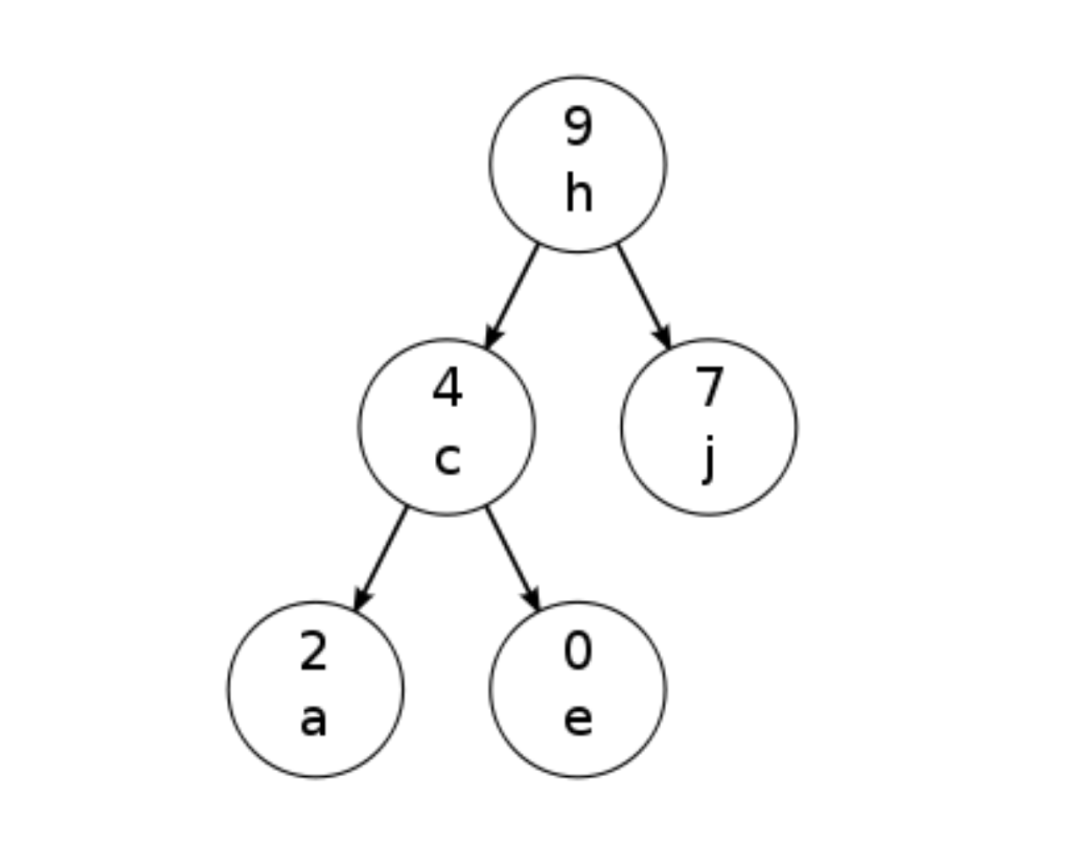
Michael Knyszek 提出这种方式具有扩展性的问题,确实,由于这棵树是mheap管理,当操作此二叉树的时候都需要维持一个lock。这在密集的对象分配以及nprocs过多的时候,会导致更长的等待时间。虽然这种情况不是特别的严重,但是这种扩展性问题不能接受。
Michael Knyszek 提出用bitmap来管理内存页,并在每个P中维护了一份page cache。这就是现在Go语言实现的方式。具体的实现细节要复杂很多,但是Knyszek 用优雅的代码展现了一位顶尖工程师的恐怖实力。

作者将这样内存管理的结构叫做基数树(radix tree), 他和一般的基数树有点不太一样,这个名字很大一部分是由于父节点包含了子节点的若干信息。
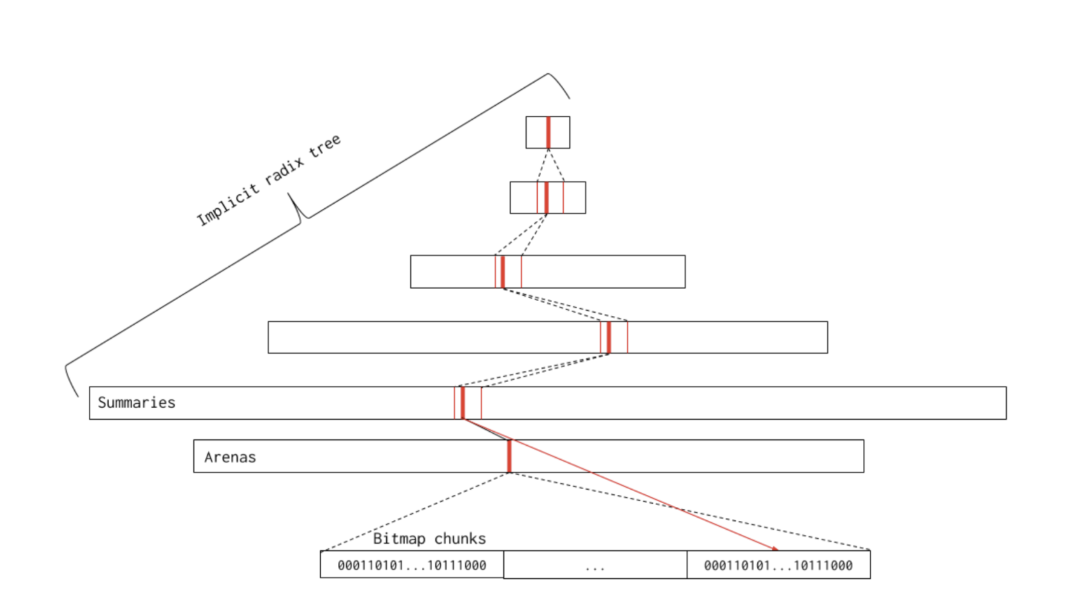
最底层的叶子节点包含了一个chunk的信息(512 * 8 K), 每一个父节点都包含了8个子节点的内存信息。这些内存信息存储在叫做summary的结构中,这个结构非常特殊,summary包含了在这个区域中空闲内存页的信息,包括了在开头有多少连续内存页,最大有多少连续内存页,在末尾有多少连续内存页。
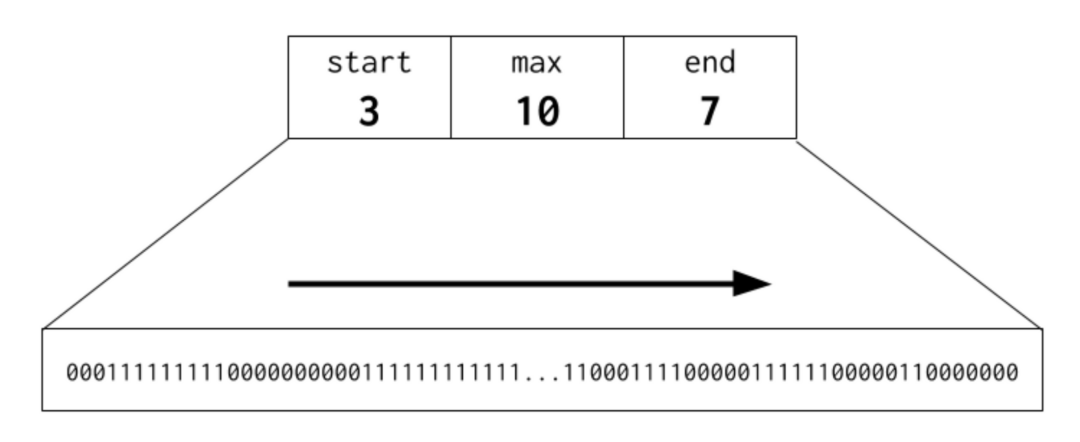
在查找的时候,这些信息非常有用,他可以快速的确定子节点是否有足够的内存。由于这棵树的结构特性,当分配的对象很大时,它能够很快的知道当前的大对象是否可以分配。如果超过了当前树的最大连续内存,就会向操作系统申请内存。
一棵树管理的内存为16G,这样一棵radix tree树有多少个呢?答案是初始化的时候大约有16384个(64位linux)。而且一个summary就uint64大小,很小的。
现在now,就可以将npages放进P的cache中,对密集小对象分配实现free-lock。现在的结构对于内存页的管理真是很细微了,而且它提供了很强的扩展性,更神奇的是,这些节点隐含了内存地址的信息,radix tree 任意一个节点都可以找到在它对应的在内存中的地址,舒服了。

推荐阅读
