图解,C语言数据结构,插入排序
之前写过的排序文章,放上链接给大家看看。

高中新生开学,需要进行军训,军训的时候,教官需要大家把按高到低排队排好。
先随机找到一个比较帅的男生做排头。
然后第二个人过来跟这个男生比身高,如果比第一个高,就排到左边,要不就排到右边。
然后第三个人过来了,他需要在原来的两个人中找到自己的位置。
……
经过把所有的人插入原来的序列,就完成了学生的身高排序。

—— 定义
插入排序顾名思义就是把未排序的数字插入到已经排序的序列的正确位置。
插入排序在很多文章中也会写作直接插入排序。
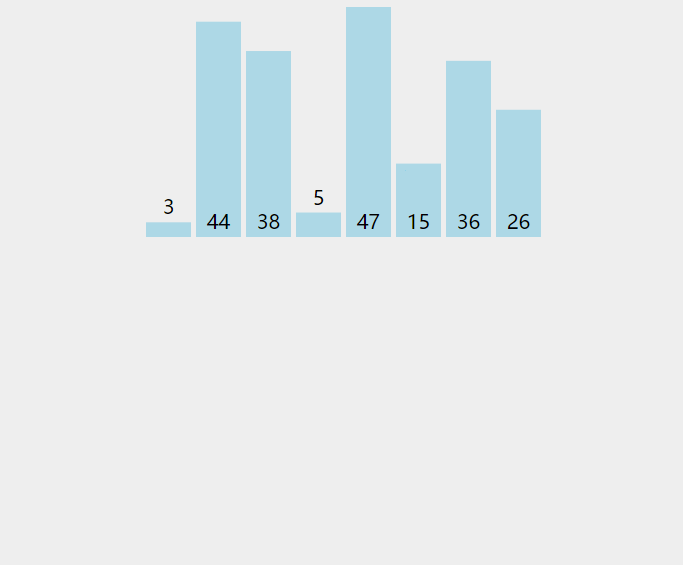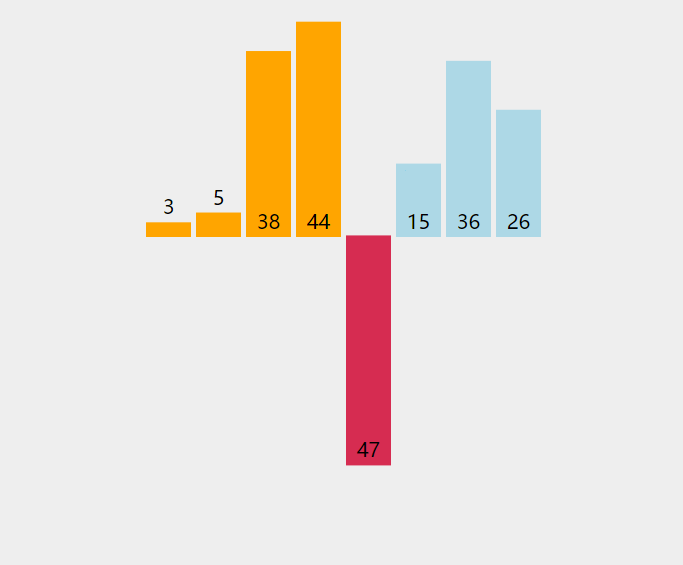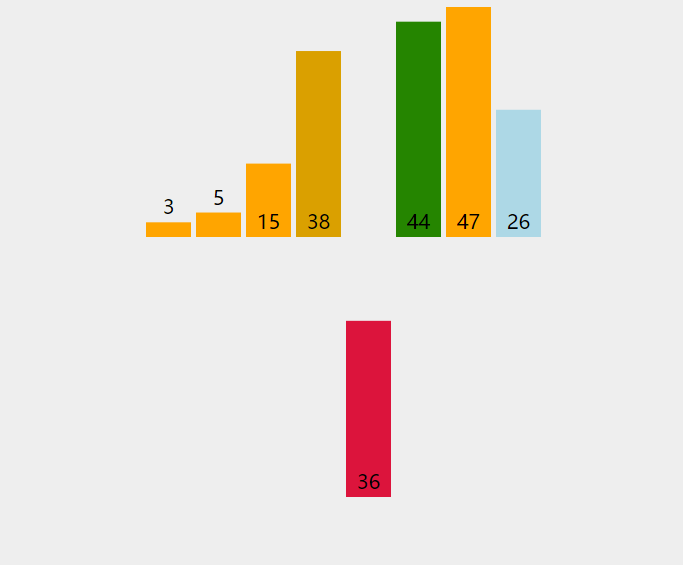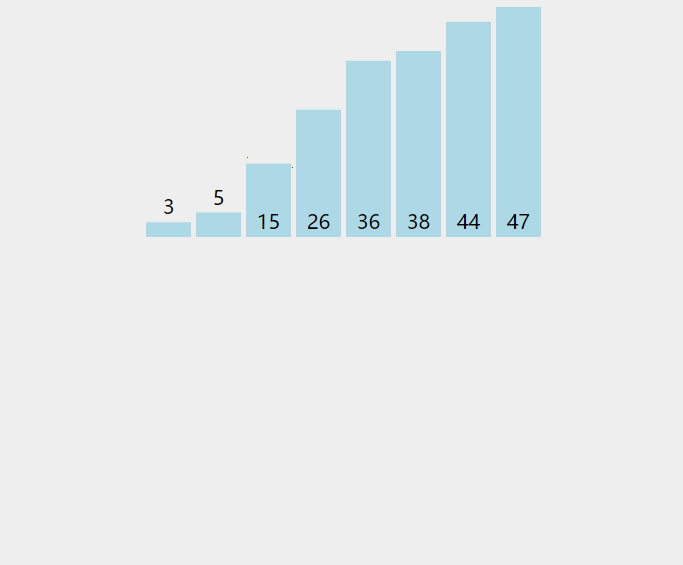
—— 用图片来举例子
比如我们需要排序这几个数字

我们首先拿出第一个数字6。
然后我们取第二个数字和第一个数字6进行排序,6被认为是已经排序好的数列,因为它就只有一个数字,当然是排序好的了。
5和6排序后,可以得到新的数列
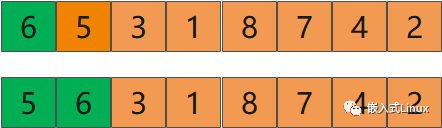
前面两个已经是排序好的序列,再拿第三个序列和前面的序列比较。
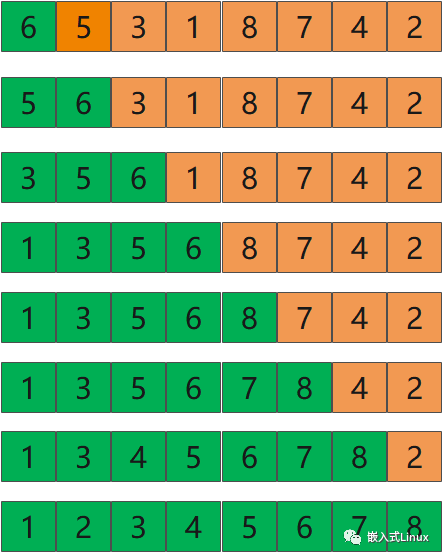
然后新排序的序列会变成这样

后面的数字都会依次插入前面已经排序好的序列,得到一个新的排序好的序列。
整个过程如下图
—— 插入排序是否是稳定的排序算法?
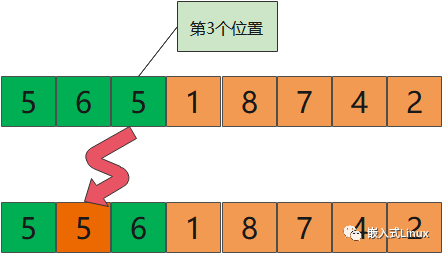
什么是稳定排序?
如果两个位置 A[j] == A[k] 相等,我们的排序算法不会改变 A[j] 和 A[k]的位置,这样的排序算法就是稳定的。
比如下面的序列,我们把数字5插入到原来的序列中,但是原来的序列中也有一个数字5,我们不改变原来数字的位置,就说明是稳定的排序。
—— 代码实现
#include
void insert_sort(int arr[], int n)
{
int i,j,temp;
/*从第一个位置开始,1~n-1,依次和前面的数据比较*/
for (i = 1; i < n; i++)
{
/*保存要插入的值*/
temp = arr[i];
/*找到需要插入数据的位置*/
for (j = i - 1; temp < arr[j] && j >= 0; --j)
{
/*把j位置的数据移动到j+1位置,向后移动一位*/
arr[j + 1] = arr[j];
}
/*插入数据*/
arr[j + 1] = temp;
}
}
#define LENGTH 8
int main()
{
int i,j;
int arr[LENGTH] = {6,5,3,1,8,7,2,4};
/*排序前*/
for(i=0;i printf("%d ",arr[i]);printf("\n");
insert_sort(arr,LENGTH);
/*排序后*/
for(i=0;i printf("%d ",arr[i]);printf("\n");
return 0;
}
看代码,是从第 1 位置开始做插入排序的,而且比较是从后往前开始比较。
比如第一个位置的数字,需要和第0个位置开始比较。
如果是第3个位置,就需要和第2、1、0这三个位置比较。
—— 代码输出
6 5 3 1 8 7 2 4
1 2 3 4 5 6 7 8
加上随机数的代码
#include
#include
#include
void insert_sort(int arr[], int n)
{
int i,j,temp;
/*从第一个位置开始,1~n-1,依次和前面的数据比较*/
for (i = 1; i < n; i++)
{
/*保存要插入的值*/
temp = arr[i];
/*找到需要插入数据的位置*/
for (j = i - 1; temp < arr[j] && j >= 0; --j)
{
/*把j位置的数据移动到j+1位置,向后移动一位*/
arr[j + 1] = arr[j];
}
/*插入数据*/
arr[j + 1] = temp;
}
}
#define LENGTH 30
int main()
{
int i,j;
int arr[LENGTH] = {6,5,3,1,8,7,2,4};
/*随机数设置种子*/
srand((unsigned)time(NULL));
/*赋值*/
for(i=0;i arr[i] = rand()%100;
/*排序前*/
for(i=0;i printf("%d ",arr[i]);printf("\n");
insert_sort(arr,LENGTH);
/*排序后*/
for(i=0;i printf("%d ",arr[i]);printf("\n");
return 0;
}
—— 代码输出
58 90 36 55 5 91 27 56 19 37 69 75 73 24 14 2 40 57 27 86 2 31 6 59 23 92 16 10 62 92
2 2 5 6 10 14 16 19 23 24 27 27 31 36 37 40 55 56 57 58 59 62 69 73 75 86 90 91 92 92
—— 算法复杂度
两个循环遍历,算法时间复杂度是 O(N^2)

评论
