1972年秋天，Vance Faber是科罗拉多大学的新教授。当两位有影响力的数学家PaulErdős和LászlóLovász来访时，Faber决定举办一场茶话会。尤其是Erdős，他是一位古怪而充满活力的研究人员，在国际上享有盛誉，Faber的同事渴望与他见面。

Erdős，Faber和Lovász将他们的讨论重点放在了超图(hypergraph)上，这在当时的图论中是一个很有前途的新想法。经过一番辩论，他们提出了一个问题，后来被称为Erdős-Faber-Lovász猜想，即在某些限制下为超图的边缘着色所需的最小颜色数。

事实证明，这个问题比预期的要难得多。

Erdős经常将这个猜想和同行分享，并为解决方案提供了奖励。数学家们逐渐意识到这个猜想的困难之处，奖励也增加到了500美元，许多数学家尝试后都失败了。

将近50年之后，5位数学家在arxiv上发布了一篇论文，他们对某些超图的边缘加阴影所需的颜色数量进行了限制，以使重叠的边缘不会具有相同的颜色。他们证明颜色的数量永远不会比超图中的顶点数量大。

论文中提出的方法留出图形的某些边缘并随机给其他边缘着色，这是研究人员近年来为解决许多长期存在的开放性问题所运用的思想的组合。

Lovász认为这篇论文是一件美丽的作品。

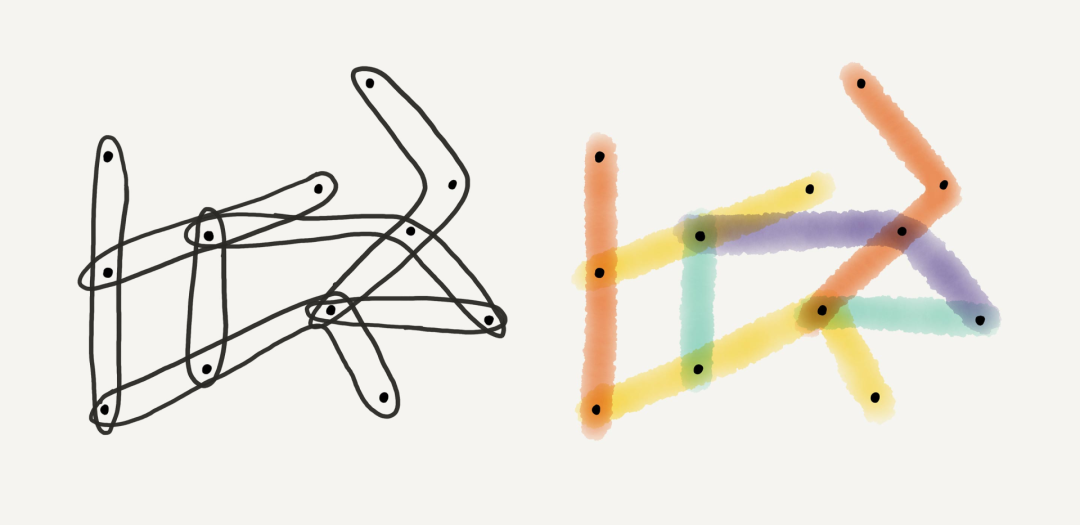
普通图是由顶点构建的，这些点由边连接。每个边正好连接两个顶点，而超图的边可以连接任意数量的顶点。

超图的边具有更广泛的概念，标准图只能表示事物对之间的关系，例如社交网络中的两个朋友（每个人都由一个顶点表示）。但是，要表达多于两个人之间的关系（例如组中的共享成员身份），每个边都需要包含多于两个人，这是超图允许的。

但是，这种多功能性是有代价的：证明超图的通用特性比普通图更难，超图模型使边着色问题变得更加困难。

着色问题的目标是为图（或超图）的所有边着色，以使在顶点处相交的两个边具有不同的颜色。为此所需的最少颜色数称为图形的色度指数(chromatic index)。

Erdős-Faber-Lovász猜想是关于特定类型的超图的着色问题，其中边重叠最少。在这些线性超图的结构中，不允许两个边在一个以上的顶点处重叠。该猜想预测线性超图的色度指数永远不会超过其顶点数。换句话说，如果线性超图具有九个顶点，则无论如何绘制，其边缘都可以使用不超过九种颜色进行着色。

Erdős-Faber-Lovász猜想的极端普遍性使其难以证明。当超图有更多顶点时，其循环边的排布方式也会成倍增加。在所有这些可能性下，似乎有些边需要比顶点多的颜色。

三种极端超图

如果您在页面上涂鸦并且绘制线性超图，则其色度索引可能会远远小于其顶点数。但是，有三种类型的极限超图推动了极限。

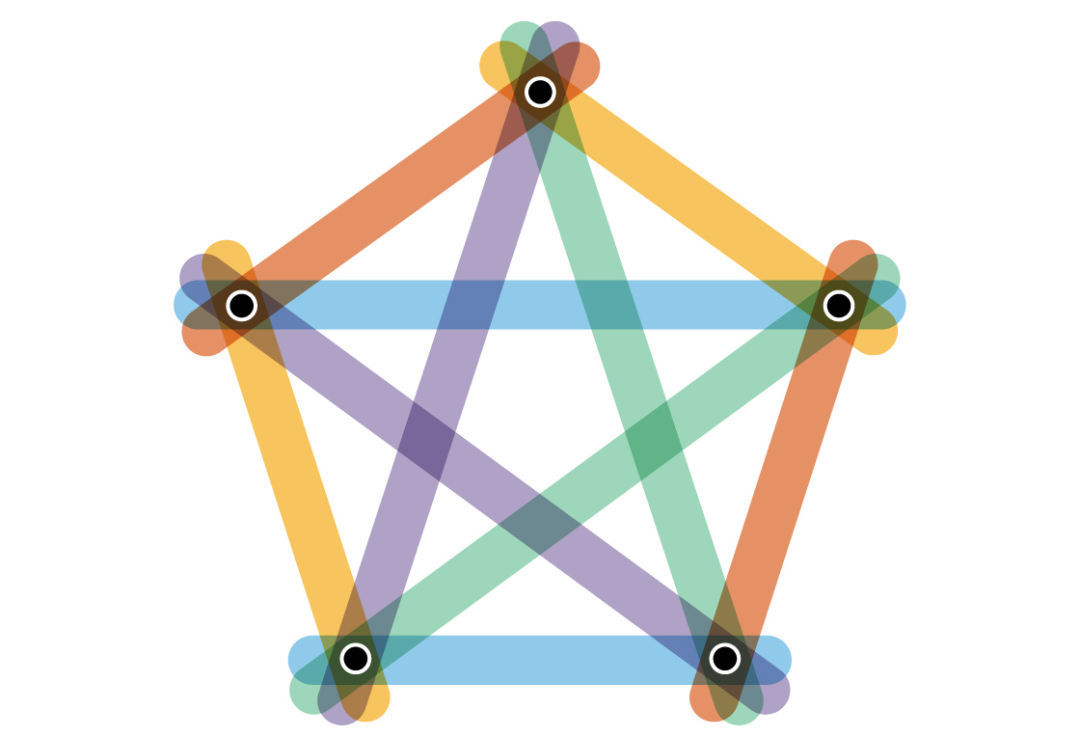
在第一个例子中，每个边仅连接两个顶点。通常将其称为完整图，因为每对顶点都是通过一条边连接的。具有奇数个顶点的完整图具有Erdős-Faber-Lovász猜想所允许的最大色度指数。

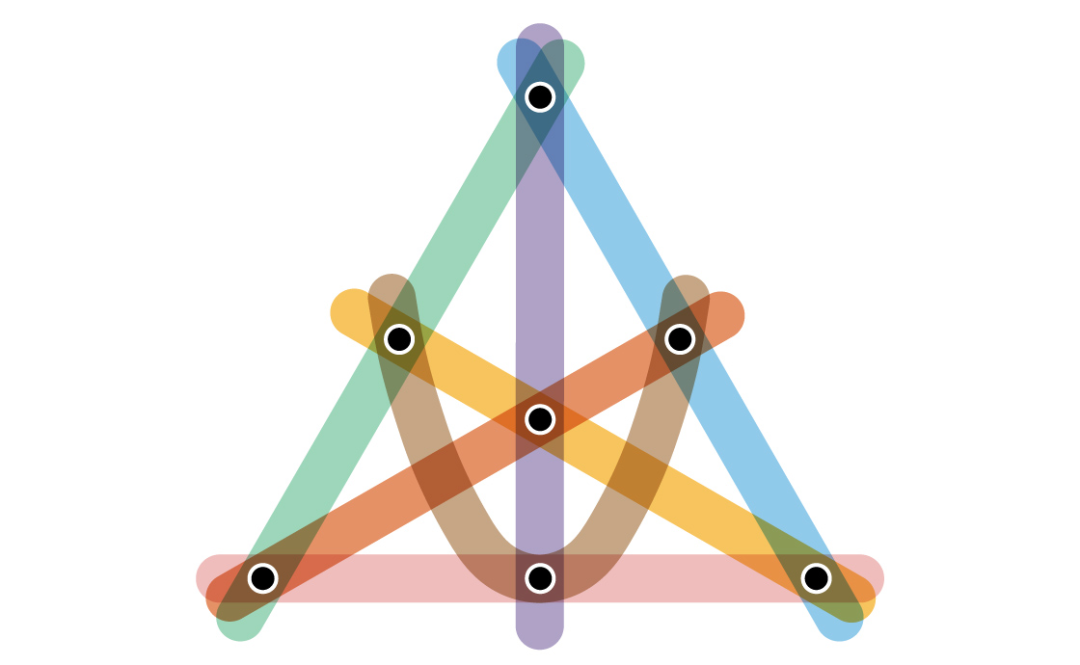
第二个例子和完整图完全不同，此类图中的所有边都连接大量顶点，随着总顶点数的增加，每个边所包含的数目也随之增加。它称为有限投影平面，并且像完整的图一样，它具有最大的色度指数。

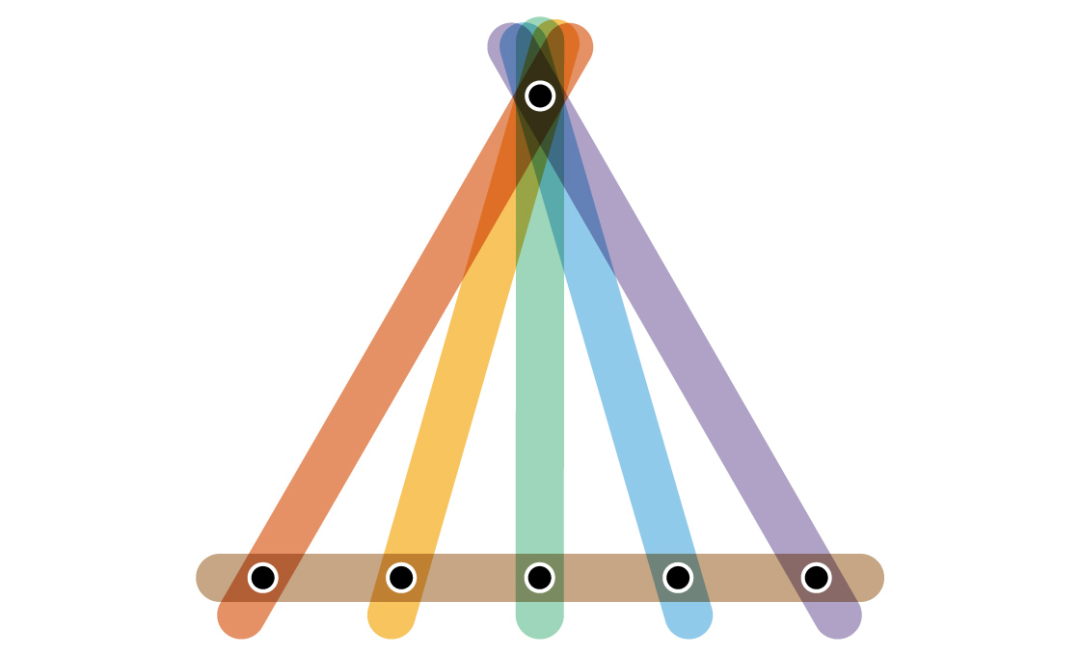
第三个例子在多种颜色的边中间仅连接两个顶点，而大边缘则连接许多顶点。在这种类型的图形中，通常会有一个特殊的顶点通过孤立的边与每个其他的顶点相连，然后是一个单独的长边，将所有其他顶点都连接起。

如果稍微修改三个极端超图之一，则结果通常也将具有最大的色度指数。这三个示例中的每一个都代表了一个更具挑战性的超图族。

要建立一个包含所有极端情况的共同定理是相当困难的。任何一个算法解决了其中一种情况，通常来说对另外两种情况都不会奏效。

虽然Erdős，Faber和Lovász知道这三个极端超图，但他们不知道是否还有其他的最大色度指数。

新的证明建立在Jeff Kahn的进步基础上，他在1992年证明了Erdős-Faber-Lovász猜想的近似版本。去年11月，Kühn和Osthus以及他们的三个博士生Kang，Kelly和Methuku着手改善Kahn的工作。

他们首先根据边连接的顶点数量将超图的边分为几个不同的类别。

排序之后，他们首先转向最难着色的边：具有最多顶点的边。

他们将这些边重新配置为普通图的顶点（每个边仅连接两个顶点）。他们使用标准图论的既定结果对它们进行着色，然后将该颜色传输回原始的超图。

迭代这个过程，直到最小边也着色完毕。小边接触的顶点较少，更易于着色。当作者到达较小的边缘时，许多可用的颜色已经在其他相邻的边缘上使用。

作者使用组合数学中的absorption作为逐渐到着色的方法，同时确保着色始终不冲突，这种技巧对于将特殊的顶点连接到第三个极限超图中的所有其他顶点特别有用，这类超图几乎使用了所有可用的颜色。

absorption提高了随机着色过程的效率，相比随机着色可能产生的颜色浪费来说，absorption能够减弱随机着色的灵活性，这是一种更精确的方法。

最后，作者提出一个算法为图的最大边着色，然后使用absorption和其他方法对较小的边着色，作者能够证明为任何线性超图的边缘着色所需的颜色数量绝不超过顶点数。这证明了Erdős-Faber-Lovász猜想是正确的。

由于概率因素，它们的证明仅适用于足够大的超图，即那些具有特定数量以上顶点的超图。这种方法在组合数学中很常见，数学家认为它几乎是完整的证明，因为它仅忽略了有限数量的超图。

Lovász认为，从本质上讲，他们已经证明了这一猜想。

为证明一个猜想而做出的努力迫使人们发现了更通用的技术，这也是从事数学的工作方式。