陶哲轩再逼近60年几何学难题!周期性密铺问题又获新突破

新智元报道

新智元报道
【新智元导读】关于60年的几何学难题周期性密铺问题,陶哲轩最近又有新突破了。
陶哲轩一直在研究的周期性密铺问题,又有新突破了。
9月18日,陶哲轩和Rachel Greenfeld将预印本论文《平移单密铺的不可判定性 (Undecidability of translational monotilings)》上传到了arXiv。
 论文地址:https://arxiv.org/abs/2309.09504
论文地址:https://arxiv.org/abs/2309.09504
这篇论文的主要结论是,如果网格的维数是无界的,那么确定网格的有限子集是否可以平铺该网格的周期子集的问题,就是不可判定的。
要知道,此问题在维度1和维度2中是可判定的。
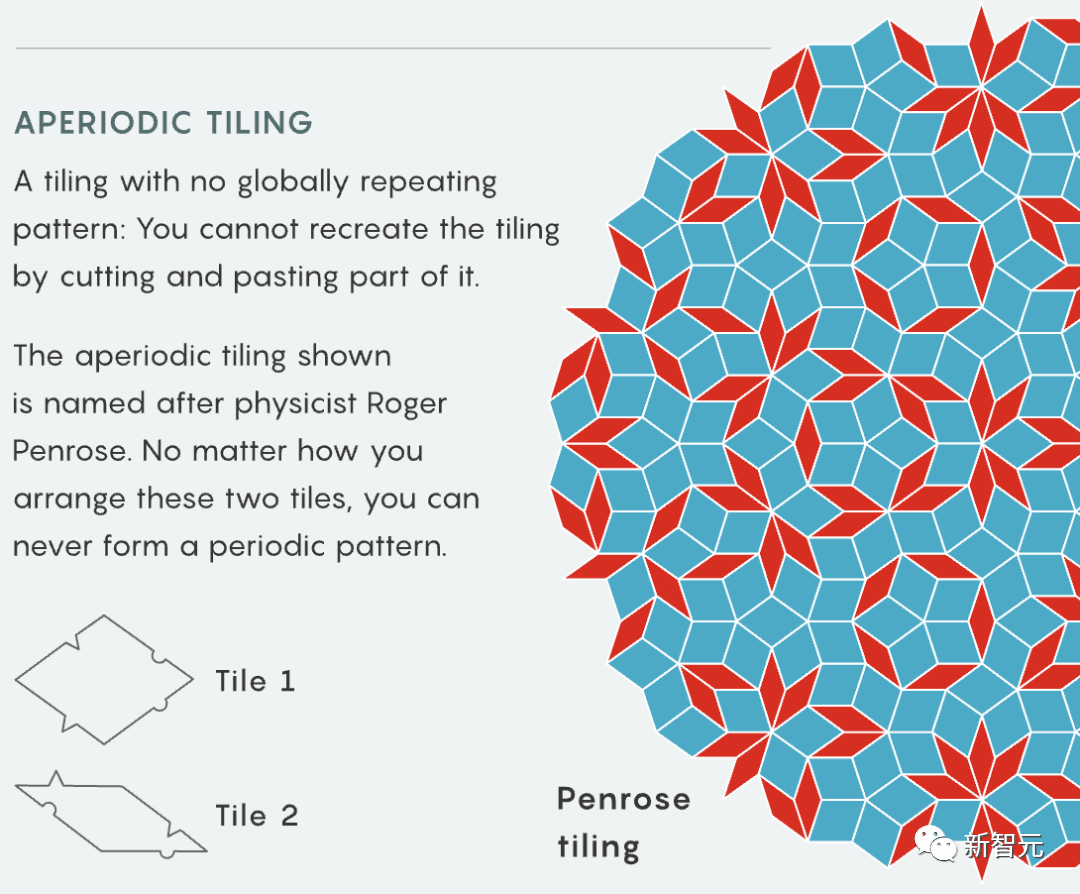
陶哲轩表示,有点奇怪的是,文中所证明的大多数组件都跟流行的游戏类似——
多米诺骨牌的密铺类似物,数独,电脑游戏「俄罗斯方块」,甚至连儿童游戏「Fizz buzz」都出现了。
为什么研究一个数学问题,会涉及到这么多游戏呢?陶哲轩也无法解释。

平移单密铺的不可判定性
在上篇论文中,他们构建了一个高维网格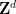 的平移单密铺
的平移单密铺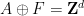
(因此单密铺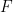 是一个有限集合 ),它是非周期性的(没有办法将这个密铺「修复」成周期性密铺
是一个有限集合 ),它是非周期性的(没有办法将这个密铺「修复」成周期性密铺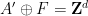 ,其中
,其中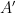 现在相对于有限索引子群
现在相对于有限索引子群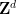 是周期性的)。
是周期性的)。

这就反驳了Stein、Grunbaum-Shephard和Lagarias-Wang的周期性密铺猜想,他们断言这种非周期性密铺单体不存在。
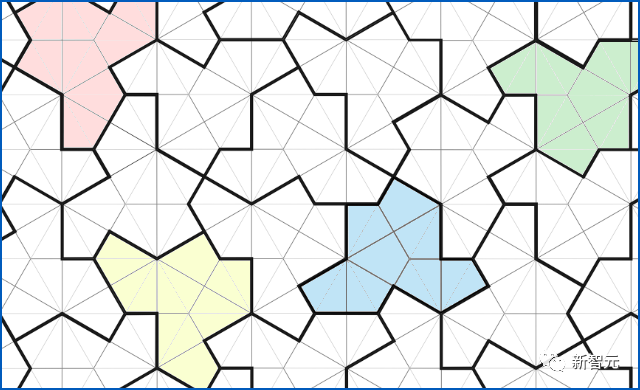
(「帽子单密铺」是一种最近发现的非周期等距单密铺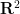 ,在这种单密铺中,可以允许使用旋转、反射以及平移,或者更新的「幽灵单片」。上述单片与帽子单密铺相似,除了不需要反射)。
,在这种单密铺中,可以允许使用旋转、反射以及平移,或者更新的「幽灵单片」。上述单片与帽子单密铺相似,除了不需要反射)。
激发陶哲轩和Rachel Greenfeld这个猜想的原因之一,是数学家Hao Wang的观察。

他发现,如果周期密铺猜想为真,那么平移密铺问题在算法上是可判定的——
有一个图灵机,对于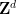 ,当给定一个维度
,当给定一个维度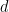 和一个有限子集
和一个有限子集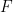 时,可以在有限的时间内确定
时,可以在有限的时间内确定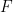 是否可以密铺
是否可以密铺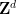 。
。
这是因为如果存在周期性密铺,就可以通过计算机搜索找到它。
如果根本不存在密铺,那么通过紧致性定理可知,存在一些有限的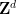 子集,这些子集不能被
子集,这些子集不能被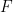 不相交的平移所覆盖,这也可以通过计算机搜索来发现。
不相交的平移所覆盖,这也可以通过计算机搜索来发现。
周期性密铺猜想断言这是仅有的两种可能的情况,从而给出了可判定性。

另一方面,Wang的论点是不可逆的:周期性密铺猜想的失败,并不自动意味着平移单密铺问题的不可判定性,因为它不排除存在一些其他算法来确定密铺,这种密铺可以不依赖于周期性密铺的存在。
(例如,即使有新发现的帽子和幽灵密铺,对于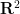 中有理系数的多边形的等距单密铺问题是否是可判定的,仍然是一个悬而未决的问题,无论它有没有反射。
中有理系数的多边形的等距单密铺问题是否是可判定的,仍然是一个悬而未决的问题,无论它有没有反射。
本文的主要结果解决了这个问题(有一个警告):

定理1
不存在任何算法,对于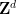 ,给定一个维度
,给定一个维度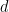 ,一个周期性子集
,一个周期性子集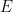 ,和一个有限子集
,和一个有限子集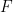 ,能在有限时间内确定是否存在一个平移密铺
,能在有限时间内确定是否存在一个平移密铺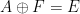 。
。
需要注意的是,必须使用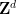 的周期性子集
的周期性子集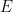 ,而不是全部的
,而不是全部的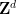 ;这在很大程度上是由于这种方法的技术限制,并且很可能通过额外的努力和创造力来消除。
;这在很大程度上是由于这种方法的技术限制,并且很可能通过额外的努力和创造力来消除。
另外,陶哲轩和Rachel Greenfeld还注意到,当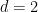 ,周期性密铺猜想是由Bhattacharya建立的,因此在
,周期性密铺猜想是由Bhattacharya建立的,因此在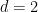 这种情况下问题可判定。
这种情况下问题可判定。
对于任何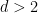 的固定值,密铺问题是否可判定仍然是开放的(注意,在上面的结果中,维度
的固定值,密铺问题是否可判定仍然是开放的(注意,在上面的结果中,维度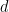 不是固定的,而是输入的一部分)。
不是固定的,而是输入的一部分)。
由于算法不可判定性和逻辑不可判定性(也称为逻辑独立性)之间存在众所周知的联系,此定理还暗示了存在一个(原则上明确可描述的)维度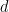 、
、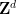 的周期性子集
的周期性子集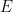 ,
,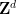 的有限子集
的有限子集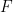 ,使得
,使得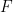 能通过平移密铺
能通过平移密铺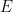 不能在ZFC集合论中被证实或证伪(当然假设这个理论是一致的)。
不能在ZFC集合论中被证实或证伪(当然假设这个理论是一致的)。
作为这种方法的结果,我们也可以在这里用「几乎二维」群 来代替
来代替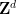 ,其中
,其中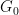 是一个有限阿贝尔群(现在成为输入的一部分,代替维度
是一个有限阿贝尔群(现在成为输入的一部分,代替维度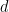 )。
)。
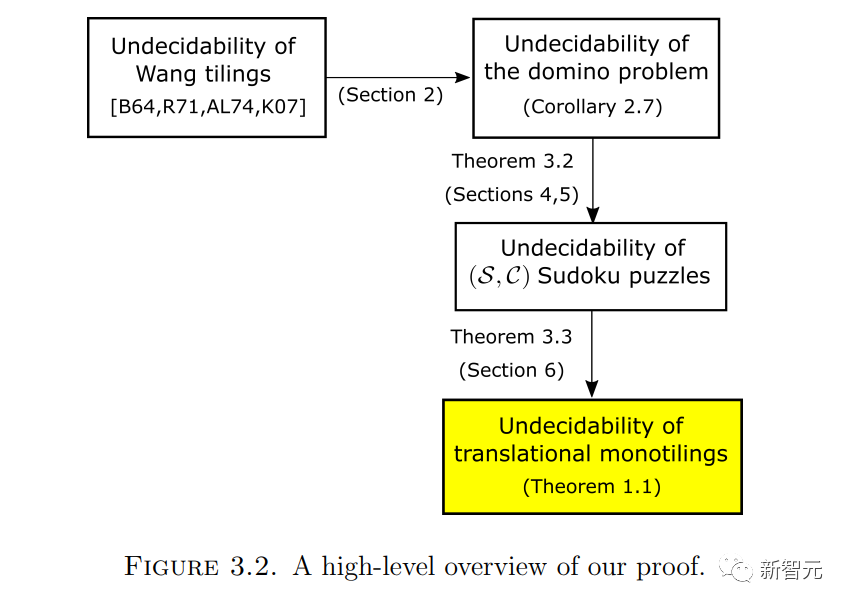
接下来,描述证明的一些主要思想。
证明某个问题不可判定的常用方法是,将已知不可判定的其他问题「编码」到原始问题中,这样,任何判定原始问题的算法也能判定嵌入的问题。
因此,我们将 Wang密铺问题编码为单密铺问题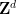 :
:

问题2(Wang密铺问题)
给定一个有限的王氏密铺集合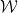 (单位正方形,每条边都从有限调色板中指定了某种颜色),是否有可能用标准的格
(单位正方形,每条边都从有限调色板中指定了某种颜色),是否有可能用标准的格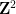 通过平移来密铺平面,使得相邻的密铺在共同边缘上具有相同的颜色?
通过平移来密铺平面,使得相邻的密铺在共同边缘上具有相同的颜色?
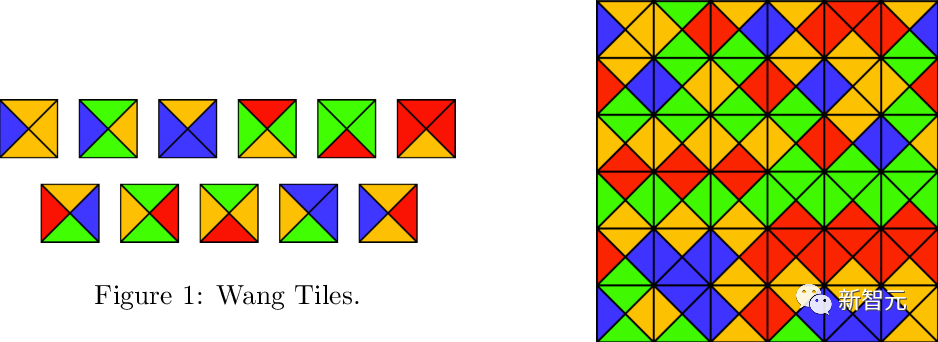
Berger曾给出一个著名的结果,即这个问题是不可判定的。
 Berger, Robert,<The undecidability of the domino problem>
Berger, Robert,<The undecidability of the domino problem>
将这一问题嵌入高维平移单密铺问题需要经过一些中间问题。
首先,我们可以很容易地将王氏密铺问题嵌入到一个类似的问题中,我们称之为多米诺骨牌问题:

问题 3(多米诺骨牌问题)
给定一个水平(或垂直)的多米诺骨牌的有限集合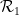 或
或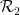 ,它们是一对相邻的单元正方形,每个单元正方形都用有限集合
,它们是一对相邻的单元正方形,每个单元正方形都用有限集合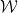 中的一个元素点来点缀,是否可以在标准格密铺
中的一个元素点来点缀,是否可以在标准格密铺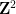 中为每个单元正方形分配一个点,使得这个密铺中的每一对水平(或垂直)的方格都能用到来自
中为每个单元正方形分配一个点,使得这个密铺中的每一对水平(或垂直)的方格都能用到来自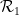 或
或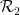 的多米诺骨牌?
的多米诺骨牌?

事实上,我们只需要将每个王氏密铺作为一个单独的「点」插入,并定义多米诺骨牌集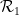 ,
,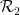 为水平或垂直相邻、边缘具有相同颜色的王氏密铺对。
为水平或垂直相邻、边缘具有相同颜色的王氏密铺对。
接下来,将多米诺骨牌问题嵌入到数独问题中:

问题 4(数独问题)
给定列宽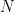 、数字集
、数字集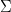 、函数
、函数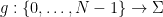 的集合
的集合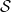 和「初始条件」
和「初始条件」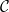 (在这里就不详细介绍了),是否可以为「数独棋盘」
(在这里就不详细介绍了),是否可以为「数独棋盘」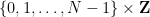 中的每个单元格
中的每个单元格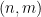 分配一个数字
分配一个数字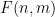 ,以便对于任何斜率
,以便对于任何斜率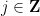 和截距
和截距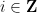 ,沿着
,沿着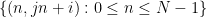 线的数字
线的数字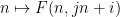 位于
位于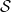 中(并且
中(并且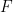 服从初始条件
服从初始条件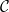 )?
)?
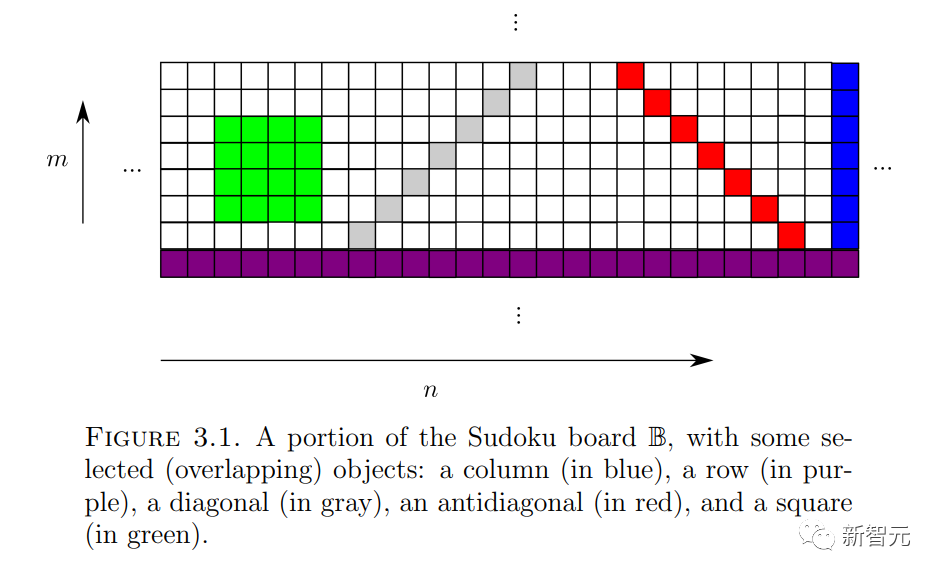
这篇论文最新颖的部分是证明了多米诺骨牌问题确实可以嵌入到数独问题中。
将数独问题嵌入到单密铺问题中,源于之前论文中修改的方法。
这些论文也引入了数独问题的版本,并创造了一种「密铺语言」,可用于把各种问题(包括数独问题)「编码」为单密铺问题。
要将多米诺骨牌问题编码为数独问题,我们需要获取一个多米诺函数
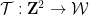 (遵守与某些多米诺骨牌集
(遵守与某些多米诺骨牌集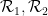 相关的多米诺骨牌约束),并使用它来构建数独函数
相关的多米诺骨牌约束),并使用它来构建数独函数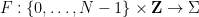 (遵守与多米诺骨牌集相关的一些数独约束);反过来说,每个遵守数独谜题规则的数独函数,都必须以某种方式从多米诺函数中产生。
(遵守与多米诺骨牌集相关的一些数独约束);反过来说,每个遵守数独谜题规则的数独函数,都必须以某种方式从多米诺函数中产生。
这种做法并不是很显而易见,但是在Emmanuel Jeandel的帮助下,陶哲轩和Rachel Greenfeld改编了Aanderaa和Lewis的一些想法,某些层次结构被用来将一个问题编码另一个问题。
在这里,我们解释分层结构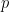 (由于多米诺骨牌问题的二维性,需要使用两个不同的素数)。
(由于多米诺骨牌问题的二维性,需要使用两个不同的素数)。
然后,通过公式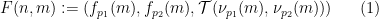 用
用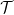 构建数独函数
构建数独函数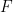 ,它将体现某种嵌入。
,它将体现某种嵌入。
其中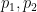 是两个不同的大素数(例如,可以取
是两个不同的大素数(例如,可以取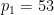 ,
,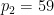 ),
),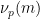 表示
表示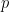 除以
除以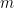 的次数,并且
的次数,并且
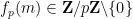 是
是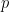 的
的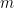 展开中的最后一个非零数字:
展开中的最后一个非零数字:
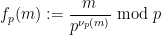
(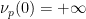 ,且
,且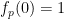 )。
)。
在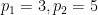 的情况下,(1) 的第一个分量如下所示:
的情况下,(1) 的第一个分量如下所示:
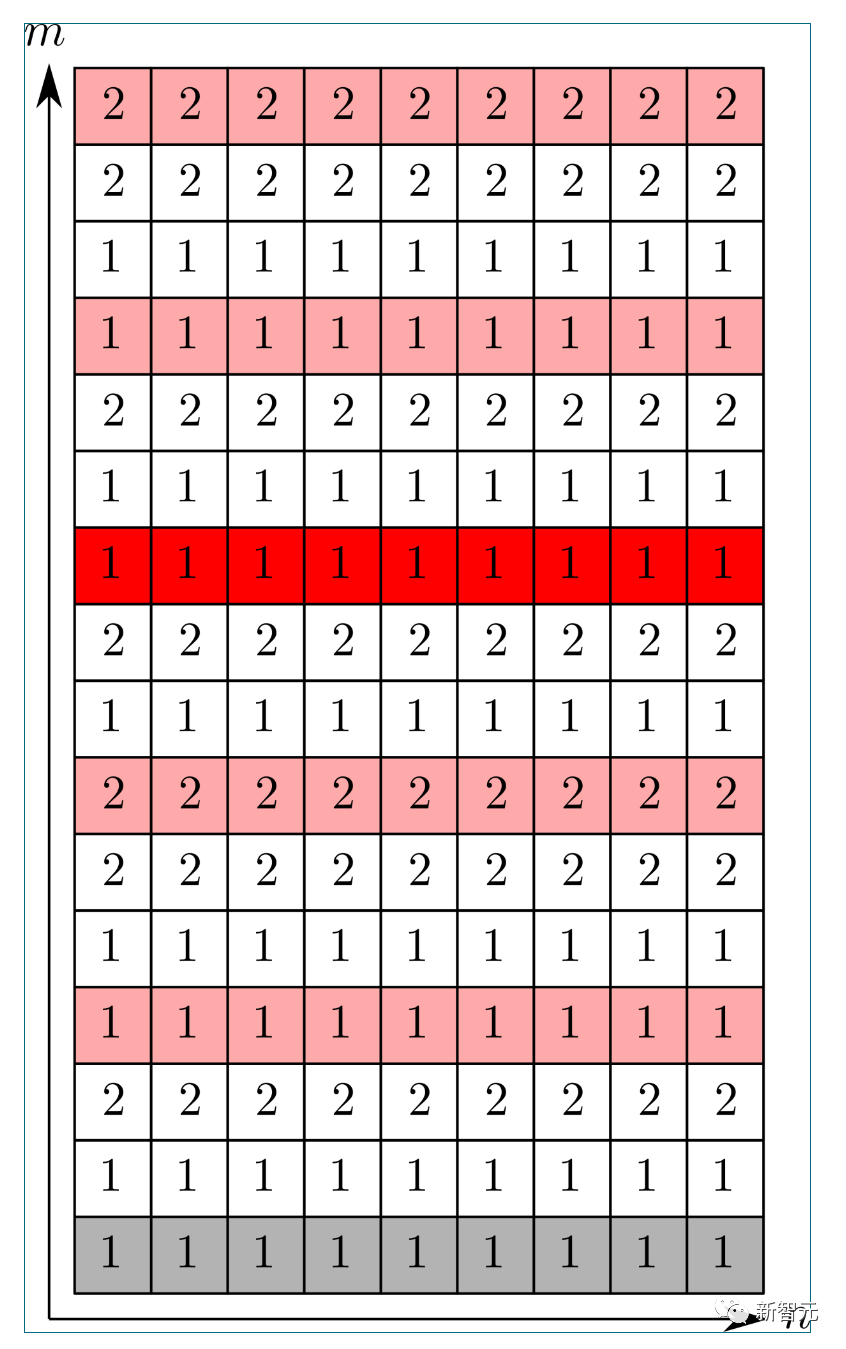
最终分量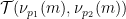 的典型实例如下所示:
的典型实例如下所示:
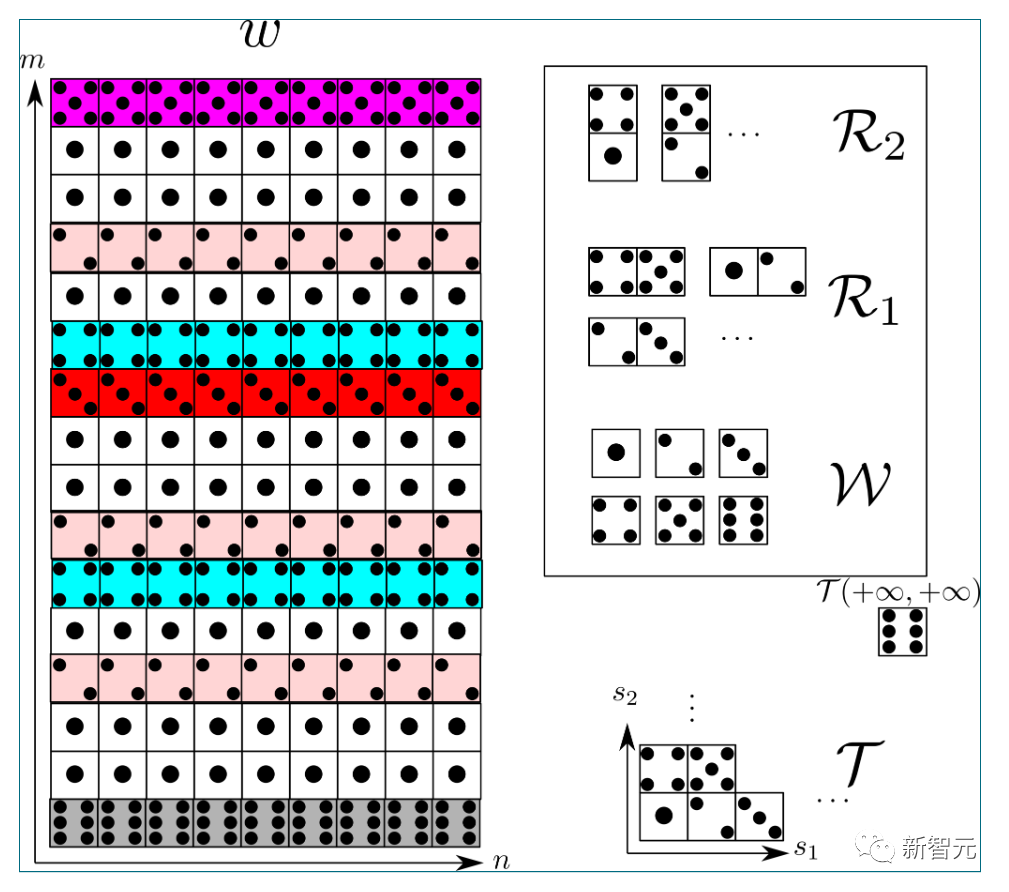
有趣的是,不知为何,这里的装饰基本上遵循了儿童游戏「Fizz buzz」的规则。



