程序员要懂的五道逻辑思维题,很有趣!

从1到100排列成一排,总共100个数,每一轮抽走奇数位置的数,问最后剩下哪个数?

先思考小规模的问题,例如从1到10,模拟整个抽取过程如下。
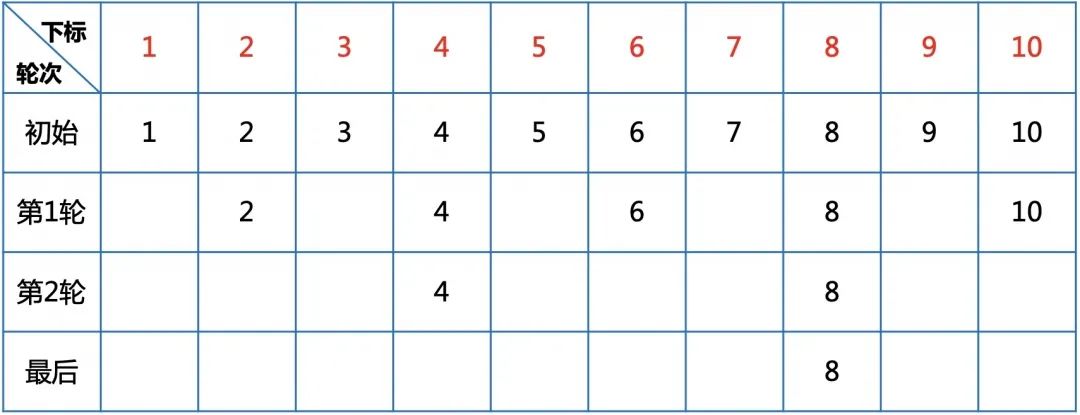
第1轮抽取完剩下所有偶数,如果都除以2,就变成了1到5的小问题;第2轮抽取后,还是剩下偶数,再除以2,变成1到2。
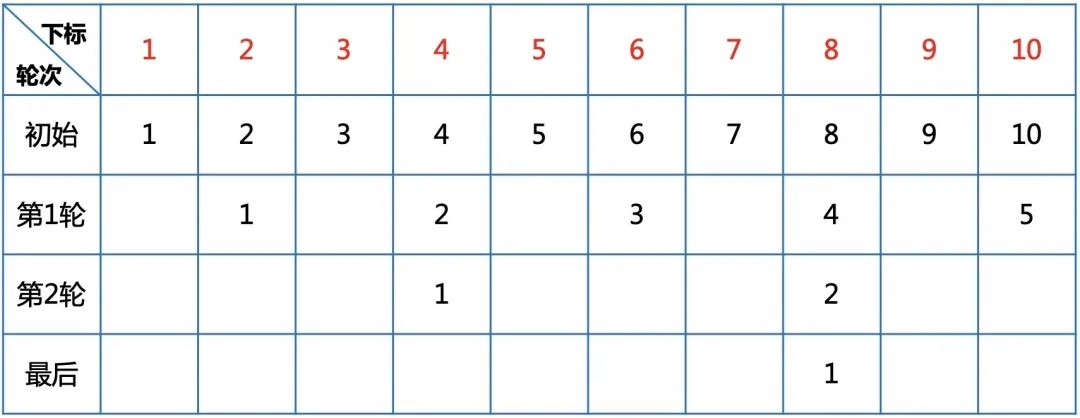
所以最后剩下的数如果因式分解,就是包含因数2最多的数。那么还原上面的问题,1到100最后剩下的数是64。
编号为1~100的灯,初始时都开着。
现进行如下操作:
编号为1的倍数的灯反方向拨一次开关。
编号为2的倍数的灯反方向拨一次开关。
...
编号为100的倍数的灯反方向拨一次开关。
问最后哪些灯是关闭的状态?
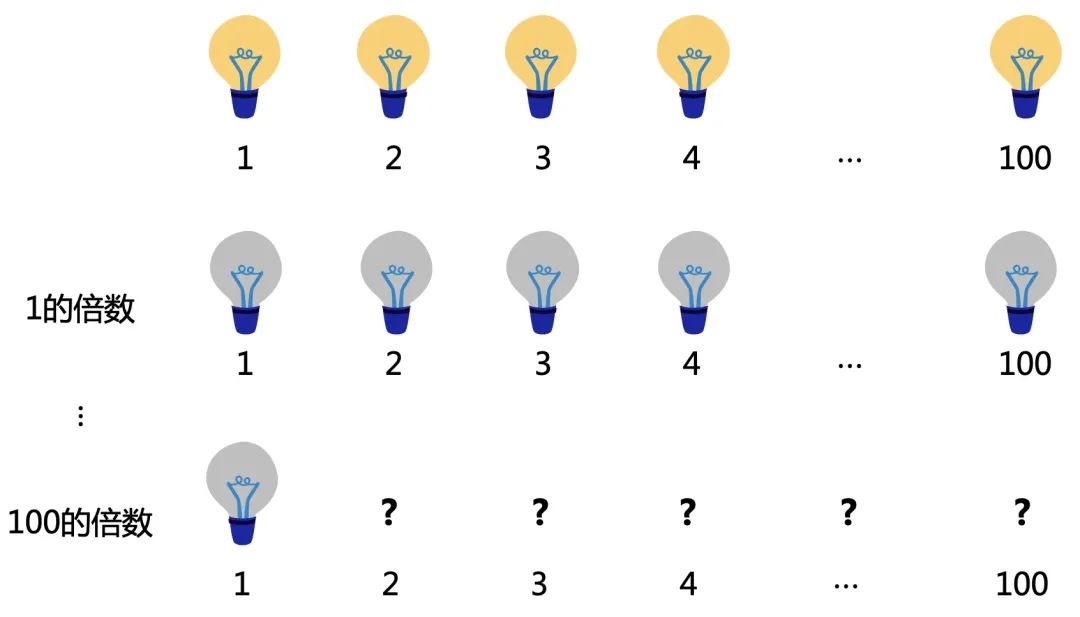
轮次数如果为灯编号的因数,那就需要操作一次开关。
而且还能得出:
操作偶数次开关,状态不变
操作奇数次开关,状态改变
所以问题就转化为判断每个灯的编号有奇数个还是偶数个因数。
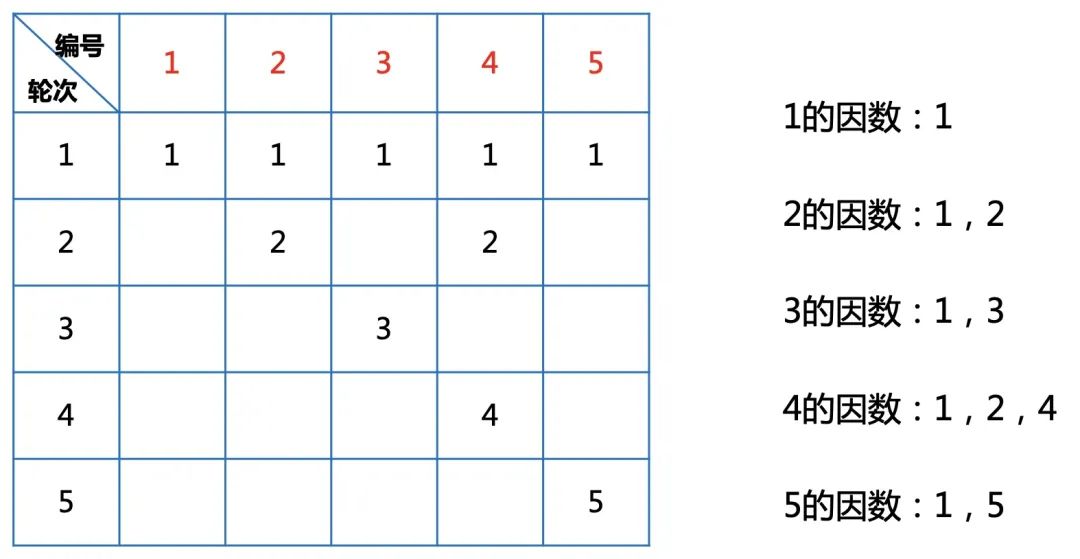
例如。
可以看出因数是对称的,如果2个因数不一样,肯定有偶数个因数。
只有能开平方的数才有奇数个因数,比如。
所以最后关闭的灯编号为1,4,9,16,25,36,49,64,81。
假设有8个球,其中有一个球偏重。给你一个天平,问最少要称几次就能找出这个偏重的球?
天平不能称出具体的重量,只能比较,所以每一次两边的球数量要一样多。
很容易就可以想到用2分的方法,先4+4,再2+2,再1+1,总共3次就可以找出来。
那有没有更少次数的方法呢?
如果第一次称3+3,有2种情况如下:
平,剩下2个球,再称一次就能找出来
不平,在重的3个球中,选择2个球1+1称一次,也能一次找出来
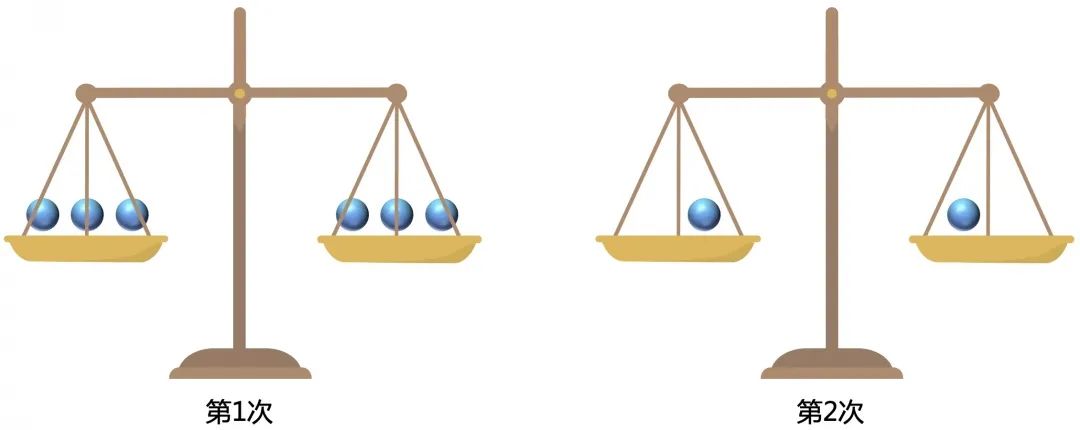
还能更少吗?答案是不能了,因为还剩下2+2或者1+1称第一次,都无法一次找出来,所以最少要两次就能找出偏重的球。
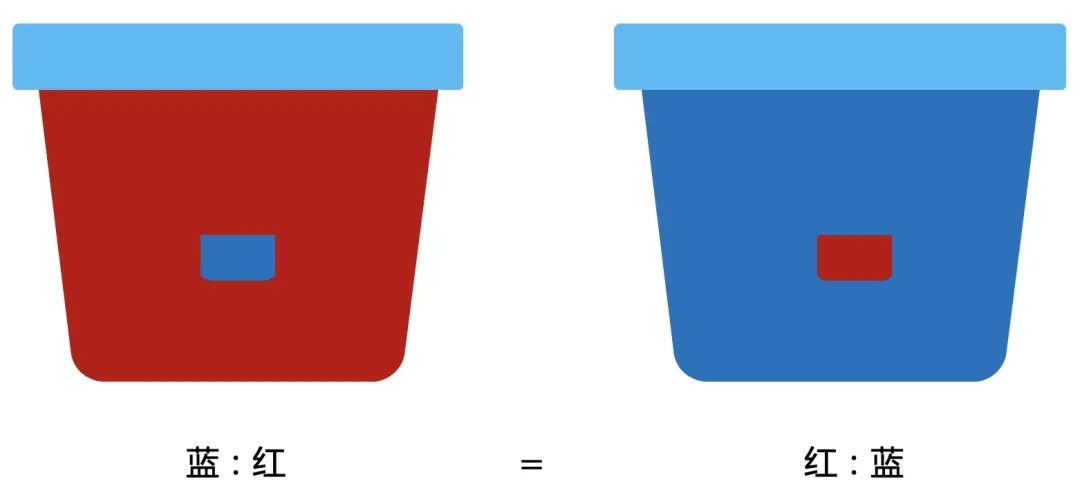
两个桶分别装了一样多的红色和蓝色的颜料。先从蓝色桶里舀一杯倒入红色中,搅拌不均匀。再从有蓝色的红色桶中舀一杯倒入蓝色桶里,问两个桶中蓝:红与红:蓝的大小关系?
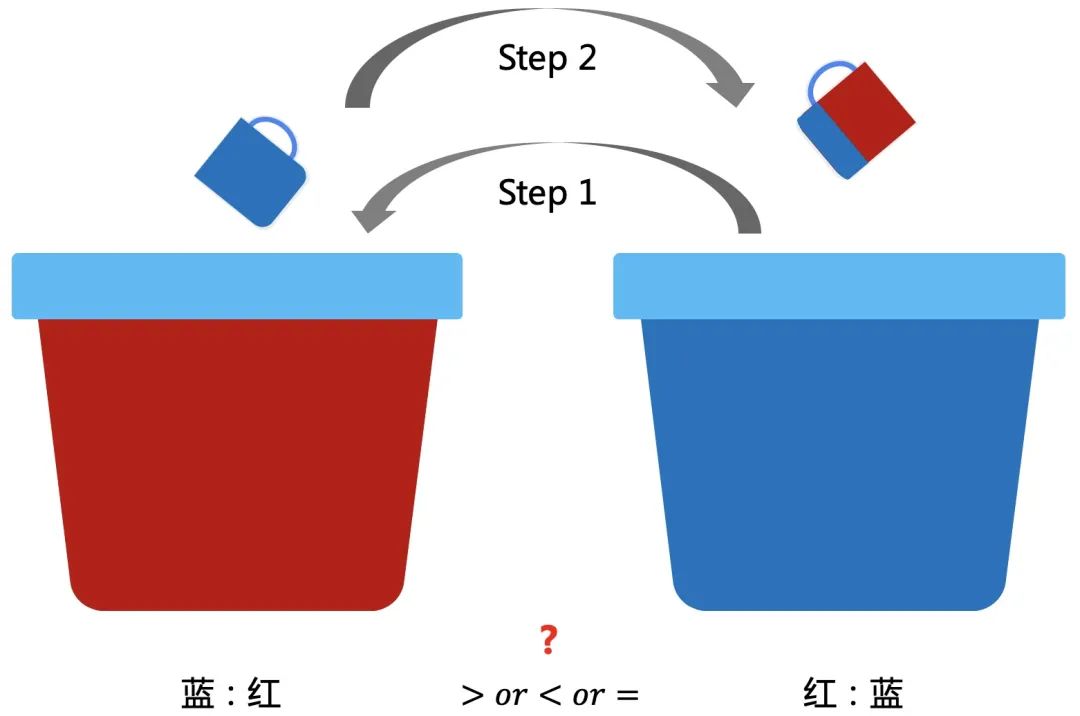
第二步舀的时候,因为不均匀,所以无法知道具体有多少比例的红色和蓝色,可以换一个角度来考虑。
因为是用的相同大小的杯子,所以两次操作后,两边的桶里的总体颜色是一样多的。假设红色里面混了一部分蓝色的颜料体积为X升,那么就有X升的红色颜料到了蓝色的桶里,所以两边的比例是一样的。
有无限多的水,给你两个杯子,容量分别为5升和6升,问如何量出3升水?

杯子没有具体的刻度,所以肯定要装满才有意义。两个杯子相差1升,所以要利用之间的差来量出其它的容量。
步骤如下:
将6升装满,再倒入5升中,剩下1升;将这1升转移到5升容量的杯子里
再将6升装满,再倒入5升中,剩下2升;将这2升转移到5升容量的杯子里
继续将6升装满,再倒入5升中,剩下3升