布隆，牛逼！布谷鸟，牛逼！

这是why的第 86 篇原创文章

在早期文章里面我曾经写过布隆过滤器：

哎，这糟糕透顶的排版，一言难尽.......

其实写文章和写代码一样。

看到一段辣眼睛的代码，正想口吐芬芳：这是哪个煞笔写的代码？

结果定睛一看，代码上写的作者居然是自己。

甚至还不敢相信，还要打开看一下 git 的提交记录。

发现确实是自己几个月前亲手敲出来，并且提交的代码。

于是默默的改掉。

出现这种情况我也常常安慰自己：没事，这是好事啊，说明我在进步。

好了，说正事。

当时的文章里面我说布隆过滤器的内部原理我说不清楚。

其实我只是懒得写而已，这玩意又不复杂，有啥说不清楚的？

布隆过滤器

布隆过滤器，在合理的使用场景中具有四两拨千斤的作用，由于使用场景是在大量数据的场景下，所以这东西类似于秒杀，虽然没有真的落地用过，但是也要说的头头是道。

常见于面试环节：比如大集合中重复数据的判断、缓存穿透问题等。

先分享一个布隆过滤器在腾讯短视频产品中的真实案例：

https://toutiao.io/posts/mtrvsx/preview

那么布隆过滤器是怎么做到上面的这些需求的呢？

首先，布隆过滤器并不存储原始数据，因为它的功能只是针对某个元素，告诉你该元素是否存在而已。并不需要知道布隆过滤器里面有那些元素。

当然，如果我们知道容器里面有哪些元素，就可以知道一个元素是否存在。

但是，这样我们需要把出现过的元素都存储下来，大数据量的情况下，这样的存储就非常的占用空间。

布隆过滤器是怎么做到不存储元素，又知道一个元素是否存在呢？

说破了其实就很简单：一个长长的数组加上几个 Hash 算法。

在上面的示意图中，一共有三个不同的 Hash 算法、一个长度为 10 的数组，数组里面存储的是 bit 位，只放 0 和 1。初始为 0。

假设现在有一个元素 [why] ，要经过这个布隆过滤器。

首先 [why] 分别经过三个 Hash 算法，得出三个不同的数字。

Hash 算法可以保证得出的数字是在 0 到 9 之间，即不超过数组长度。

我们假设计算结果如下：

• Hash1(why)=1
• Hash2(why)=4
• Hash3(why)=8

对应到图片中就是这样的：

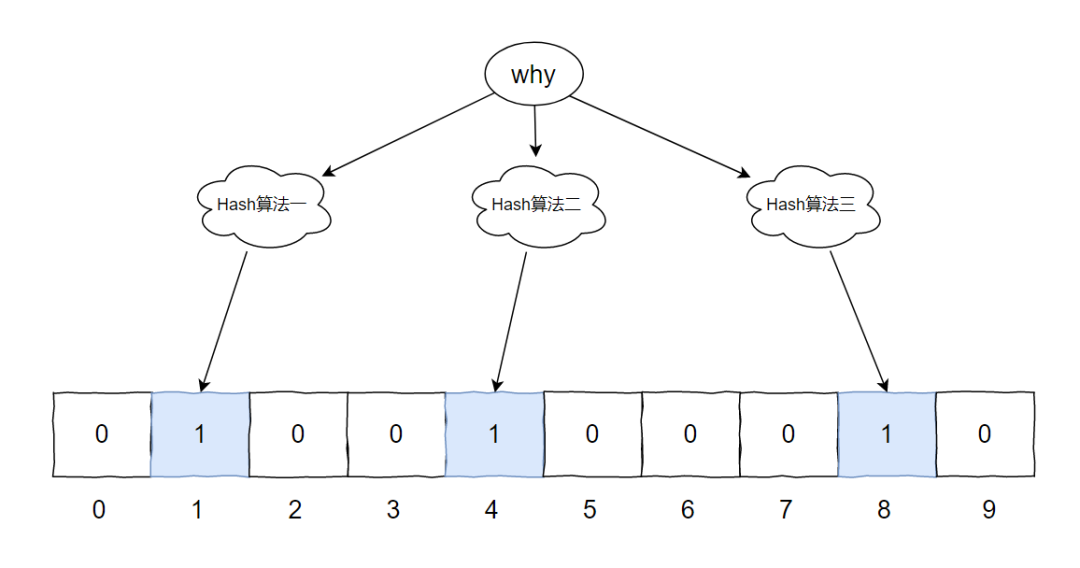
这时，如果 [why] 又来了，经过 Hash 算法得出的下标还是 1,4,8，发现数组对应的位置上都是 1。表明这个元素极有可能出现过。

注意，这里说的是极有可能。也就是说会存在一定的误判率。

我们先再存入一个元素 [jay]。

• Hash1(jay)=0
• Hash2(jay)=5
• Hash3(jay)=8

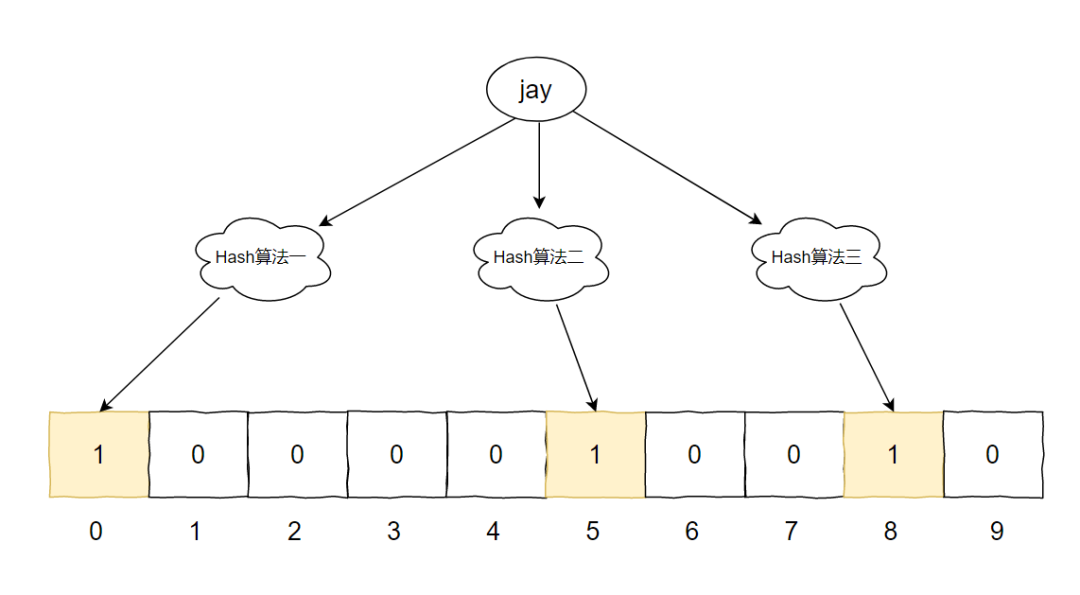
此时，我们把两个元素汇合一下，就有了下面这个图片：

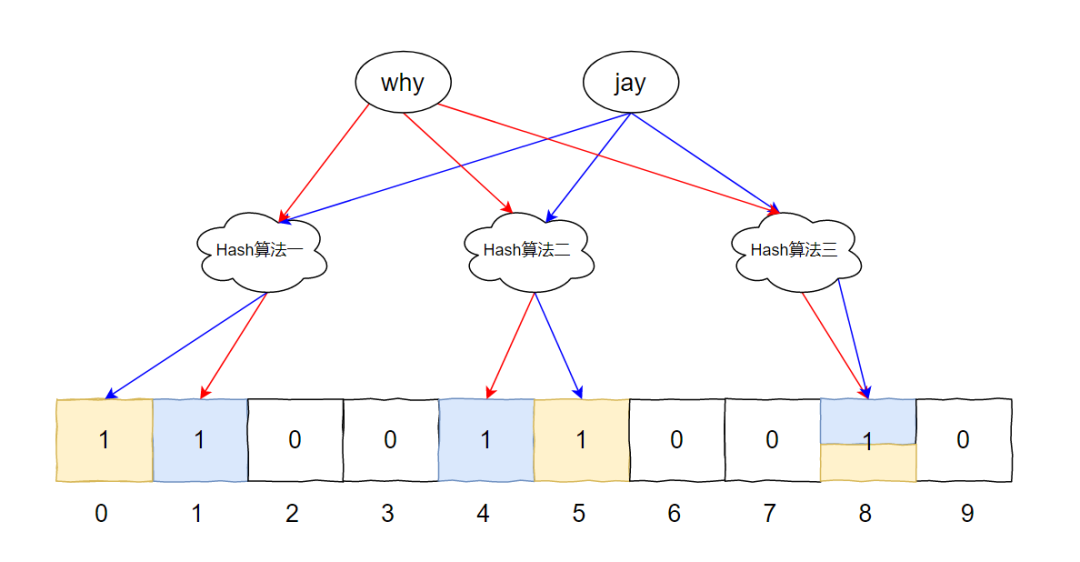
其中的下标为 8 的位置，比较特殊，两个元素都指向了它。

这个图片这样看起来有点难受，我美化一下：

好了，现在这个数组变成了这样：

你说，你只看这个玩意，你能知道这个过滤器里面曾经有过 why 和 jay 吗？

别说你不知道了，就连过滤器本身都不知道。

现在，假设又来了一个元素 [Leslie]，经过三个 Hash 算法，计算结果如下：

• Hash1(Leslie)=0
• Hash2(Leslie)=4
• Hash3(Leslie)=5

通过上面的元素，可以知道此时 0,4,5 这三个位置上都是 1。

布隆过滤器就会觉得这个元素之前可能出现过。于是就会返回给调用者：[Leslie]曾经出现过。

但是实际情况呢？

其实我们心里门清，[Leslie] 不曾来过。

这就是误报的情况。

这就是前面说的：布隆过滤器说存在的元素，不一定存在。

而一个元素经过某个 hash 计算后，如果对应位置上的值是 0，那么说明该元素一定不存在。

但是它有一个致命的缺点，就是不支持删除。

为什么？

假设要删除 [why]，那么就要把 1,4,8 这三个位置置为 0。

但是你想啊，[jay] 也指向了位置 8 呀。

如果删除 [why] ，位置 8 变成了 0，那么是不是相当于把 [jay] 也移除了？

为什么不支持删除就致命了呢？

你又想啊，本来布隆过滤器就是使用于大数据量的场景下，随着时间的流逝，这个过滤器的数组中为 1 的位置越来越多，带来的结果就是误判率的提升。从而必须得进行重建。

所以，文章开始举的腾讯的例子中有这样一句话：

除了删除这个问题之外，布隆过滤器还有一个问题：查询性能不高。

因为真实场景中过滤器中的数组长度是非常长的，经过多个不同 Hash 函数后，得到的数组下标在内存中的跨度可能会非常的大。跨度大，就是不连续。不连续，就会导致 CPU 缓存行命中率低。

这玩意，这么说呢。就当八股文背起来吧。

踏雪留痕，雁过留声，这就是布隆过滤器。

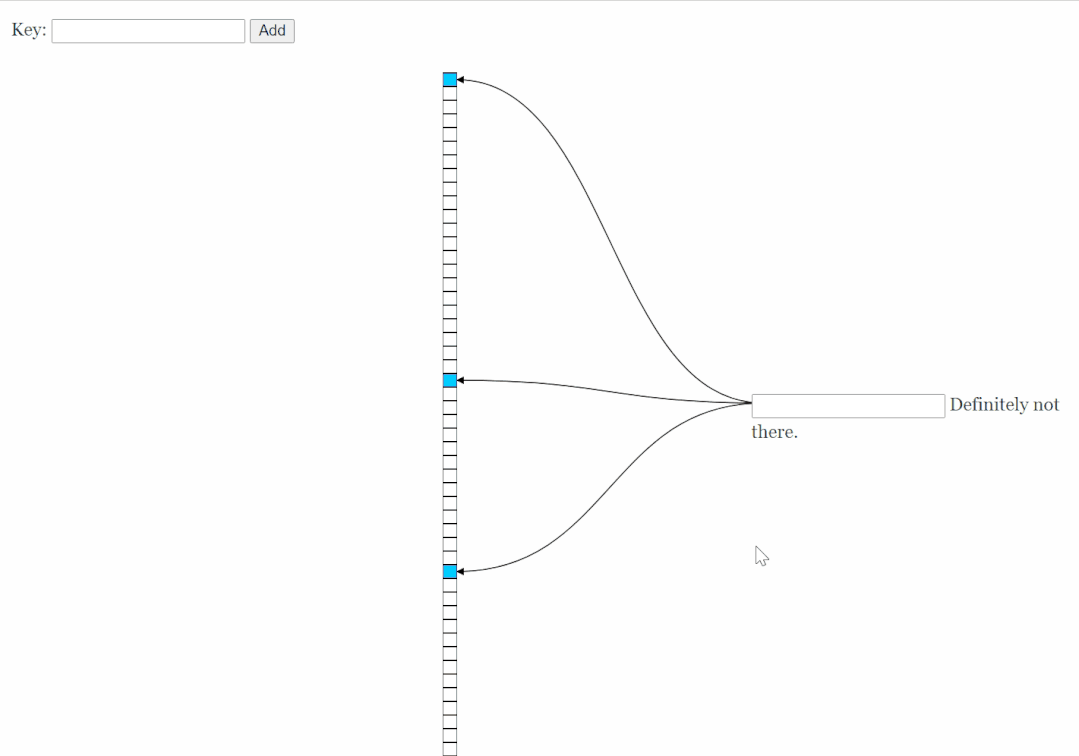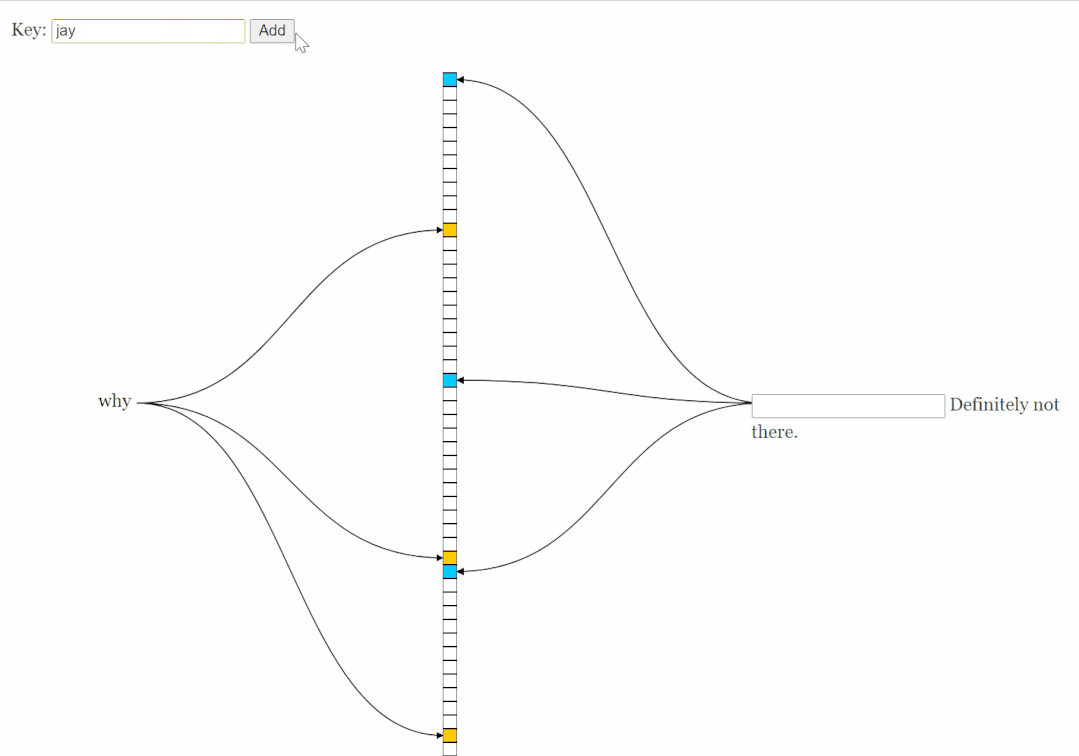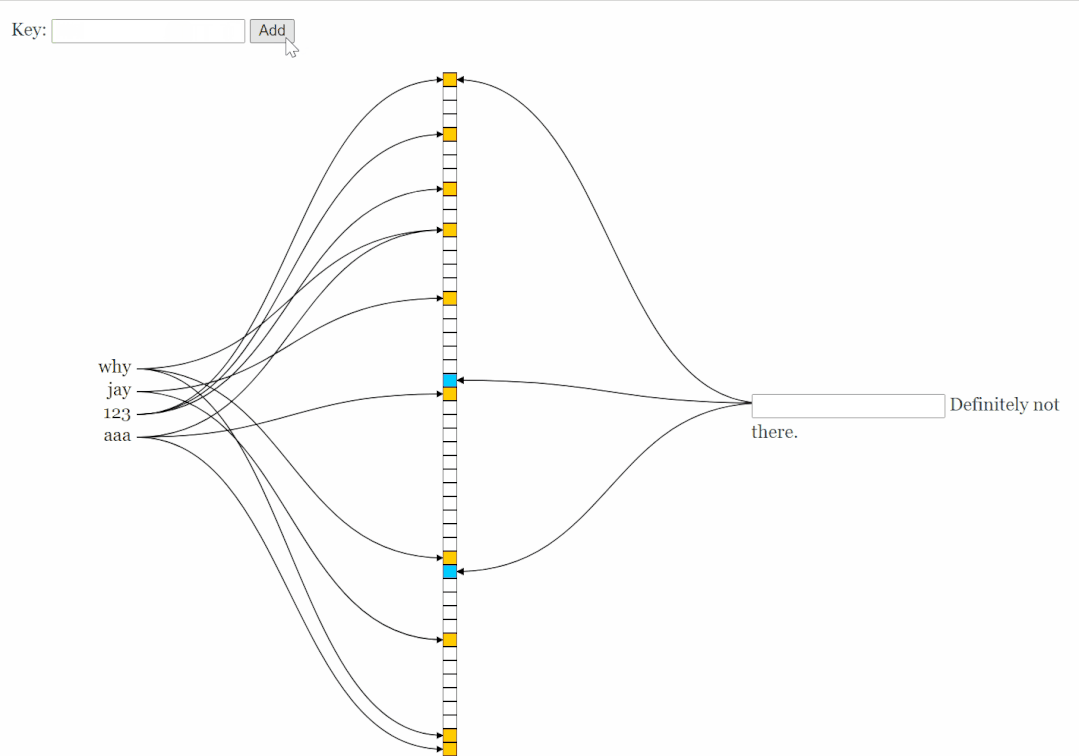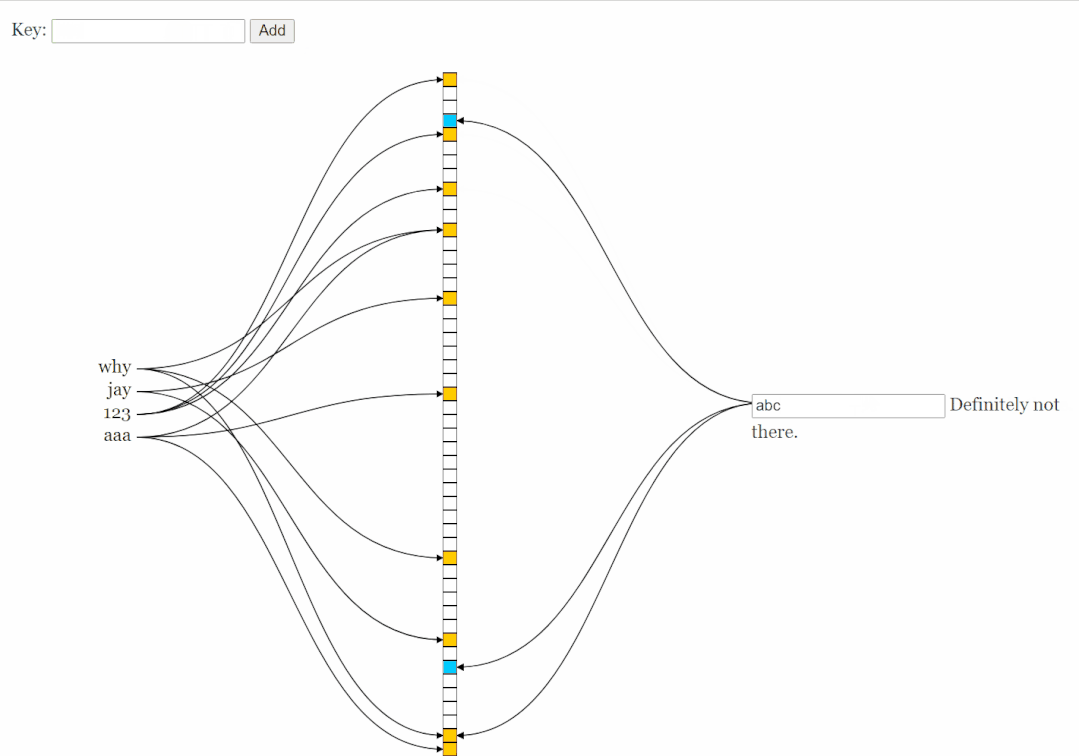
如果你想玩一下布隆过滤器，可以访问一下这个网站：

https://www.jasondavies.com/bloomfilter/

左边插入，右边查询：

如果要布隆过滤器支持删除，那么怎么办呢？

有一个叫做 Counting Bloom Filter。

它用一个 counter 数组，替换数组的比特位，这样一比特的空间就被扩大成了一个计数器。

用多占用几倍的存储空间的代价，给 Bloom Filter 增加了删除操作。

这也是一个解决方案。

但是还有更好的解决方案，那就是布谷鸟过滤器。

另外，关于布隆过滤器的误判率，有一个数学推理公式。很复杂，很枯燥，就不讲了，有兴趣的可以去了解一下。

http://pages.cs.wisc.edu/~cao/papers/summary-cache/node8.html

布谷鸟 hash

布谷鸟过滤器，第一次出现是在 2014 年发布的一篇论文里面：《Cuckoo Filter: Practically Better Than Bloom》

https://www.cs.cmu.edu/~dga/papers/cuckoo-conext2014.pdf

但是在讲布谷鸟过滤器之前，得简单的铺垫一下 Cuckoo hashing，也就是布谷鸟 hash 的知识。

因为这个词是论文的关键词，在文中出现了 52 次之多。

Cuckoo hashing，最早出现在这篇 2001 年的论文之中：

https://www.cs.tau.ac.il/~shanir/advanced-seminar-data-structures-2009/bib/pagh01cuckoo.pdf

主要看论文的这个地方：

它的工作原理，总结起来是这样的：

它有两个 hash 表，记为 T1，T2。

两个 hash 函数，记为 h1，h2。

当一个不存在的元素插入的时候，会先根据 h1 计算出其在 T1 表的位置，如果该位置为空则可以放进去。

如果该位置不为空，则根据 h2 计算出其在 T2 表的位置，如果该位置为空则可以放进去。

如果该位置不为空，就把当前位置上的元素踢出去，然后把当前元素放进去就行了。

也可以随机踢出两个位置中的一个，总之会有一个元素被踢出去。

被踢出去的元素怎么办呢？

没事啊，它也有自己的另外一个位置。

论文中的伪代码是这样的：

看不懂没关系，我们画个示意图：

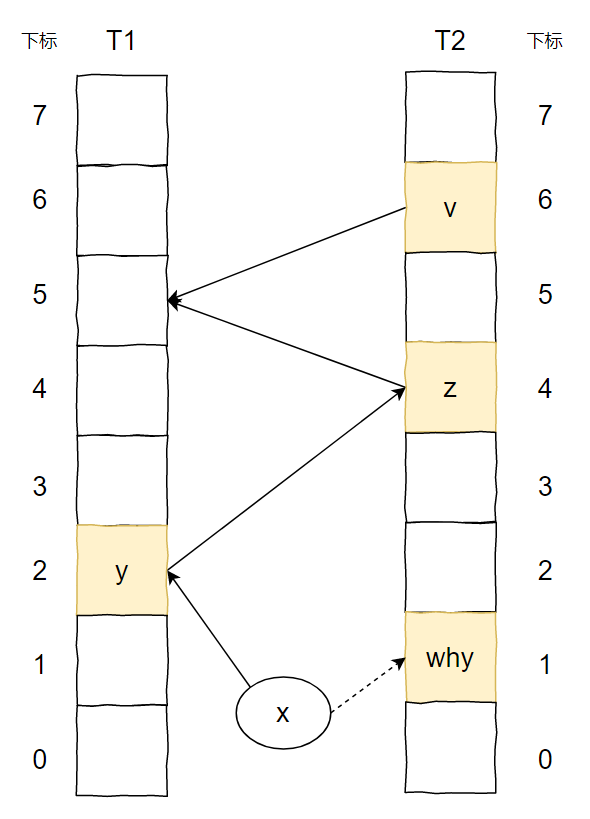
上面的图说的是这样的一个事儿：

我想要插入元素 x，经过两个 hash 函数计算后，它的两个位置分别为 T1 表的 2 号位置和 T2 表的 1 号位置。

两个位置都被占了，那就随机把 T1 表 2 号位置上的 y 踢出去吧。

而 y 的另一个位置被 z 元素占领了。

于是 y 毫不留情把 z 也踢了出去。

z 发现自己的备用位置还空着（虽然这个备用位置也是元素 v 的备用位置），赶紧就位。

所以，当 x 插入之后，图就变成了这样：

上面这个图其实来源就是论文里面（a）：

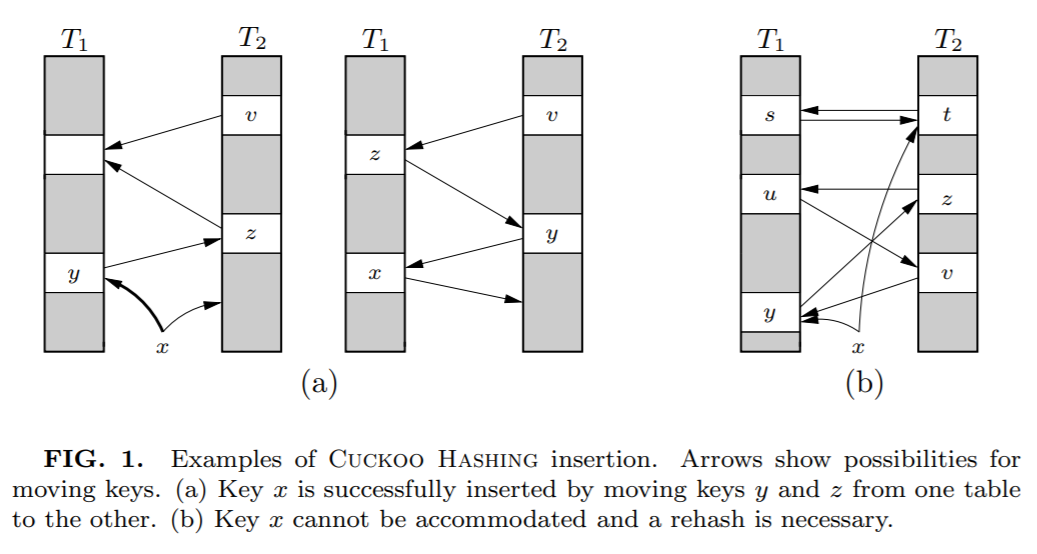
这种类似于套娃的解决方式看是可行，但是总是有出现循环踢出导致放不进 x 的问题。

比如上图中的（b）。

当遇到这种情况时候，说明布谷鸟 hash 已经到了极限情况，应该进行扩容，或者 hash 函数的优化。

所以，你再次去看伪代码的时候，你会明白里面的 MaxLoop 的含义是什么了。

这个 MaxLoop 的含义就是为了避免相互踢出的这个过程执行次数太多，设置的一个阈值。

其实我理解，布谷鸟 hash 是一种解决 hash 冲突的骚操作。

如果你想上手玩一下，可以访问这个网站：

http://www.lkozma.net/cuckoo_hashing_visualization/

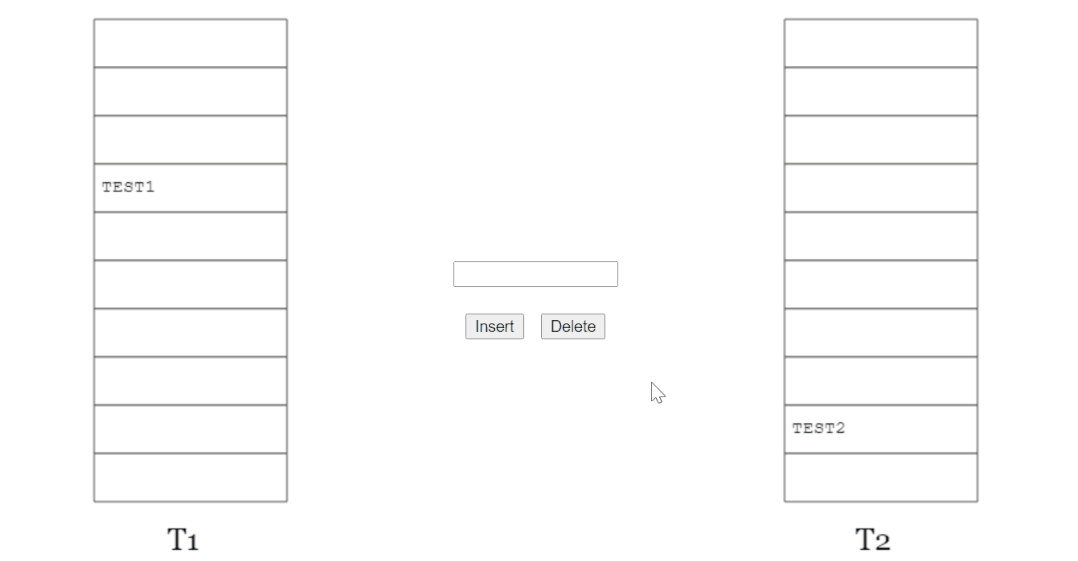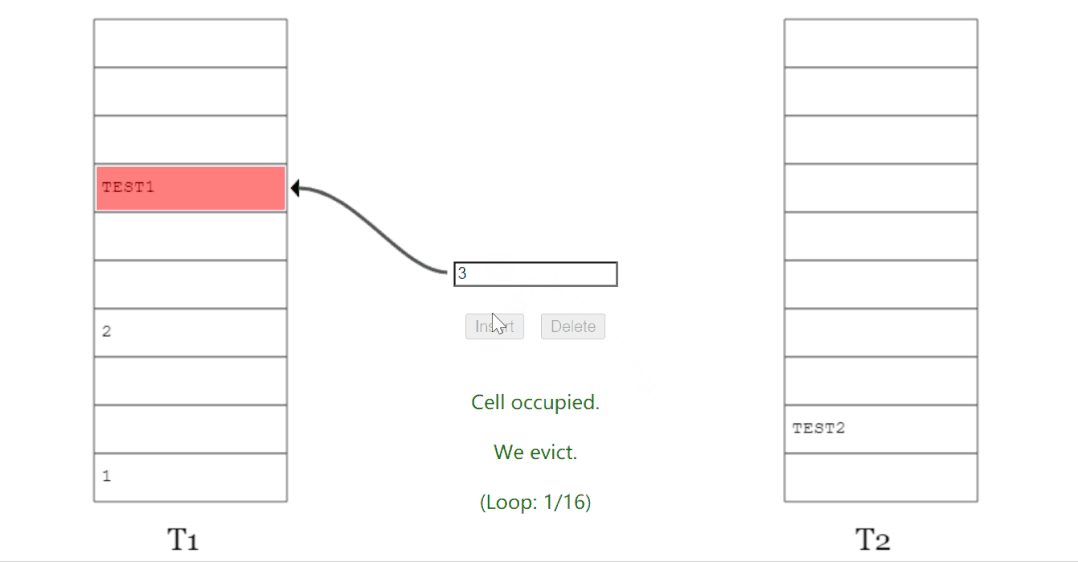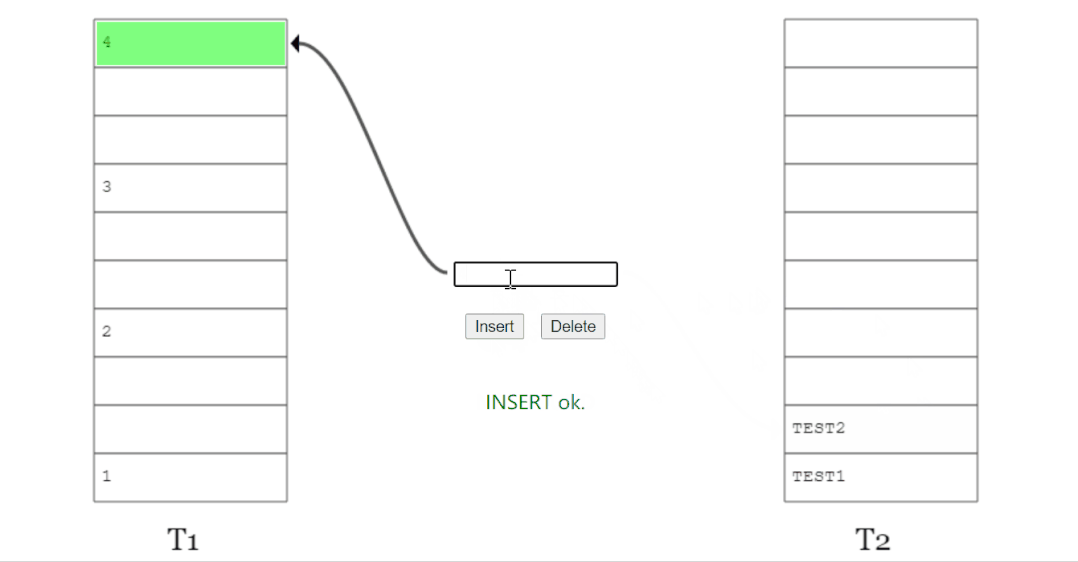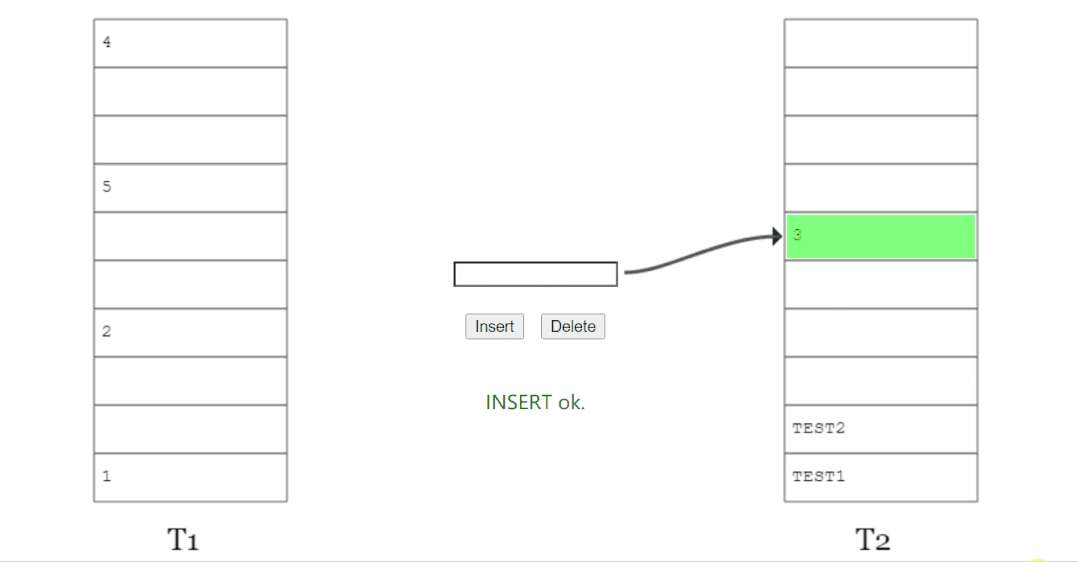
当踢来踢去了 16 （MaxLoop）次还没插入完成后，它会告诉你，需要 rehash 并对数组扩容了：

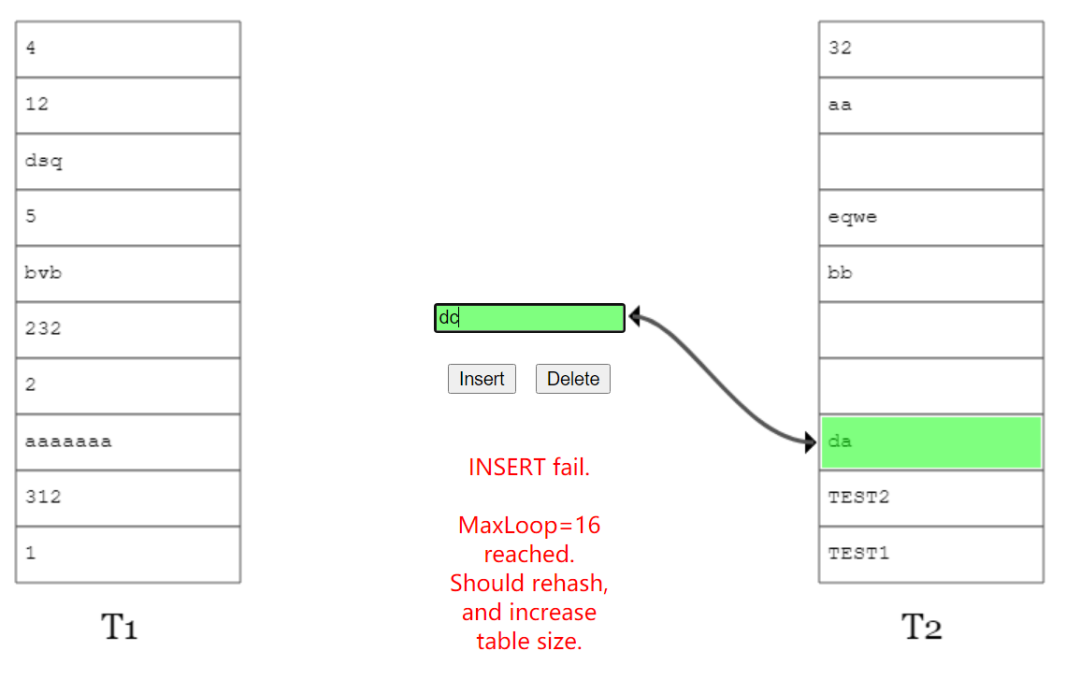
布谷鸟 hash 就是这么一回事，一场踢来踢去的游戏。

接着，我们看布谷鸟过滤器。

布谷鸟过滤器

布谷鸟过滤器的论文《Cuckoo Filter: Practically Better Than Bloom》开篇第一页，里面有这样一段话。

直接和布隆过滤器正面刚：我布谷鸟过滤器，就是比你屌一点。

上来就指着别人的软肋怼：

标准的布隆过滤器的一大限制是不能删除已经存在的数据。如果使用它的变种，比如 Counting Bloom Filter，但是空间却被撑大了 3 到 4 倍，巴拉巴拉巴拉......

而我就比较骚了：

这篇论文将要证明的是，与标准布隆过滤器相比，我支持删除，在空间或性能上并不需要更高的开销。

我，布谷鸟过滤器是一个实用的数据结构，提供了四大优势：

• 1.支持动态的新增和删除元素。
• 2.提供了比传统布隆过滤器更高的查找性能，即使在空间接近满的情况下（比如空间利用率达到 95% 的时候）。
• 3.比诸如商过滤器（quotient filter，另一种过滤器）之类的替代方案更容易实现。
• 4.如果要求错误率小于 3%，那么在许多实际应用中，它比布隆过滤器占用的空间更小。

布谷鸟过滤器的 API 无非就是插入、查询和删除嘛。

其中最重要的就是插入，看一下：

论文中的部分，你大概瞟一眼，看不明白没关系，我这不是马上给你分析一波吗。

插入部分的伪代码，可以看到一点布谷鸟 hash 的影子，因为就是基于这个东西来的。

那么最大的变化在什么地方呢？

无非就是 hash 函数的变化。

看的我目瞪狗呆，心想：

首先，我们回忆一下布谷鸟 hash，它存储的是插入元素的原始值，比如 x。

x 会经过两个 hash 函数，如果我们记数组的长度为 L，那么就是这样的：

• p1 = hash1(x) % L
• p2 = hash2(x) % L

非常容易理解，是我认知范围内的东西。

而布谷鸟过滤器计算位置是怎样的呢？

• h1(x) = hash(x),
• h2(x) = h1(x) ⊕ hash(x’s fingerprint).

我们可以看到，计算 h2（位置2）时，对 x 的 fingerprint 进行了一个 hash 计算。

“指纹”的概念一会再说，我们先关注位置的计算。

这题就稍微有点超纲了，我慢慢说。

上面算法中的异或运算确保了一个重要的性质：位置 h2 可以通过位置 h1 和 h1 中存储的“指纹”计算出来。

说人话就是：只要我们知道一个元素的位置（h1）和该位置里面存储的“指纹”信息，那么我们就可以知道该“指纹”的备用位置（h2）。

因为使用的异或运算，所以这两个位置具有对偶性。

由于具有对偶性，那么其实我们只要知道其中的任意一个位置，就能知道对应的另外一个位置。

只要保证 hash(x’s fingerprint) !=0，那么就可以确保 h2!=h1，也就可以确保不会出现自己踢自己的死循环问题。

另外，为什么要对“指纹”进行一个 hash 计算之后，在进行异或运算呢？

论文中给出了一个反证法：如果不进行 hash 计算，假设“指纹”的长度是 8bit，那么其对偶位置算出来，距离当前位置最远也才 256。

为啥，论文里面写了：

因为如果“指纹”的长度是 8bit，那么异或操作只会改变当前位置 h1(x) 的低 8 位，高位不会改变。

就算把低 8 位全部改了，算出来的位置也就是我刚刚说的：最远 256 位。

所以，对“指纹”进行哈希处理可确保被踢出去的元素，可以重新定位到哈希表中完全不同的存储桶中，从而减少哈希冲突并提高表利用率。

然后这个 hash 函数还有个问题你发现了没？

它没有对数组的长度进行取模，那么它怎么保证计算出来的下标一定是落在数组中的呢？

这个就得说到布谷鸟过滤器的另外一个限制了。

其强制数组的长度必须是 2 的指数倍。

2 的指数倍的二进制一定是这样的：10000000...（n个0）。

这个限制带来的好处就是，进行异或运算时，可以保证计算出来的下标一定是落在数组中的。

这个限制带来的坏处就是：

• 布谷鸟过滤器：我支持删除操作。
• 布隆过滤器：我不需要限制长度为 2 的指数倍。
• 布谷鸟过滤器：我查找性能比你高。
• 布隆过滤器：我不需要限制长度为 2 的指数倍。
• 布谷鸟过滤器：我空间利用率也高。
• 布隆过滤器：我不需要限制长度为 2 的指数倍。
• 布谷鸟过滤器：我烦死了，TMD！

接下来，说一下“指纹”。

这是论文中第一次出现“指纹”的地方。

“指纹”其实就是插入的元素进行一个 hash 计算，而 hash 计算的产物就是几个 bit 位。

布谷鸟过滤器里面存储的就是元素的“指纹”。

查询数据的时候，就是看看对应的位置上有没有对应的“指纹”信息：

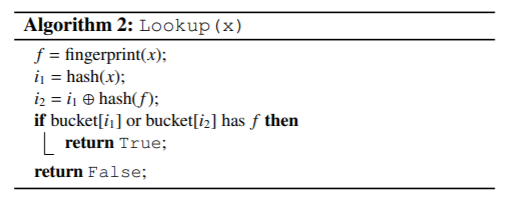
删除数据的时候，也只是抹掉该位置上的“指纹”而已：

由于是对元素进行 hash 计算，那么必然会出现 hash 碰撞的问题，也就是“指纹”相同的情况，也就是会出现误判的情况。

没有存储原数据，所以牺牲了数据的准确性，但是只保存了几个 bit，因此提升了空间效率。

说到空间利用率，你想想布谷鸟 hash 的空间利用率是多少？

在完美的情况下，也就是没有发生哈希冲突之前，它的空间利用率最高只有 50%。

因为没有发生冲突，说明至少有一半的位置是空着的。

除了只存储“指纹”，布谷鸟过滤器还能怎么提高它的空间利用率的呢？

看看论文里面怎么说的：

前面的 (a)、(b) 很简单，还是两个 hash 函数，但是没有用两个数组来存数据，就是基于一维数组的布谷鸟 hash ，核心还是踢来踢去，不多说了。

重点在于 (c)，对数组进行了展开，从一维变成了二维。

每一个下标，可以放 4 个元素了。

你可以理解为之前一个下标是一个圆板凳，上面只能放一个屁股。

而现在你可以把一个下标看成一个四方桌，可以坐四个人，打麻将了。

这样一个小小的转变，空间利用率从 50% 直接到了 98%：

我就问你怕不怕？

上面截图的论文中的第一点就是在陈诉这样一个事实：

当 hash 函数固定为 2 个的时候，如果一个下标只能放一个元素，那么空间利用率是 50%。

但是如果一个下标可以放 2，4，8 个元素的时候，空间利用率就会飙升到 84%，95%，98%。

到这里，我们明白了布谷鸟过滤器对布谷鸟 hash 的优化点和对应的工作原理。

看起来一切都是这么的完美。

各项指标都比布隆过滤器好，主打的是支持删除的操作。

但是真的这么好吗？

当我看到论文第六节的这一段的时候，沉默了：

对重复数据进行限制：如果需要布谷鸟过滤器支持删除，它必须知道一个数据插入过多少次。不能让同一个数据插入 kb+1 次。其中 k 是 hash 函数的个数，b 是一个下标的位置能放几个元素。

比如 2 个 hash 函数，一个二维数组，它的每个下标最多可以插入 4 个元素。那么对于同一个元素，最多支持插入 8 次。

例如下面这种情况：

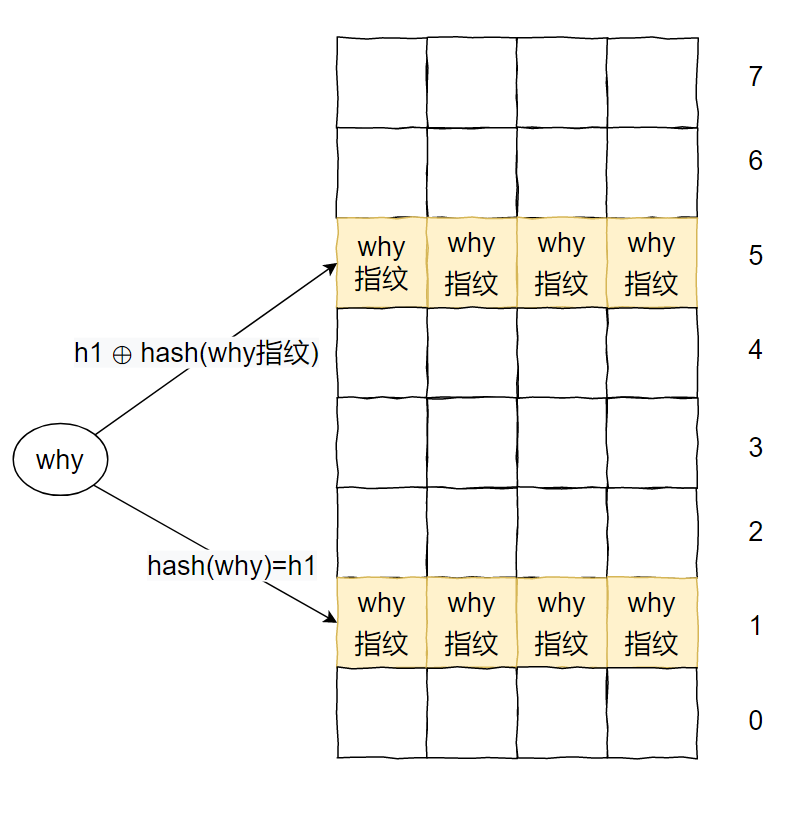
why 已经插入了 8 次了，如果再次插入一个 why，则会出现循环踢出的问题，直到最大循环次数，然后返回一个 false。

怎么避免这个问题呢？

我们维护一个记录表，记录每个元素插入的次数就行了。

虽然逻辑简单，但是架不住数据量大呀。你想想，这个表的存储空间又怎么算呢？

想想就难受。

如果你要用布谷鸟过滤器的删除操作，那么这份难受，你不得不承受。

最后，再看一下各个类型过滤器的对比图吧：

还有，其中的数学推理过程，不说了，看的眼睛疼，而且看这玩意容易掉头发。

荒腔走板

你知道为什么叫做“布谷鸟”吗？

布谷鸟，又叫杜鹃。

《本草纲目》有这样的记载：“鸤鸠不能为巢，居他巢生子”。这里描述的就是杜鹃的巢寄生行为。巢寄生指的是鸟类自己不筑巢，把卵产在其他种类鸟类的巢中，由宿主代替孵化育雏的繁殖方式，包括种间巢寄生（寄生者和宿主为不同物种）和种内巢寄生（寄生者和宿主为同一物种）。现今一万多种鸟类中，有一百多种具有巢寄生的行为，其中最典型的就是大杜鹃。

就是说它自己把蛋下到别的鸟巢中，让别的鸟帮它孵小鸡。哦不，孵小鸟。

小杜鹃孵出来了后，还会把同巢的其他亲生鸟蛋推出鸟巢，好让母鸟专注于喂养它。

我的天呐，这也太残忍了吧。

但是这个“推出鸟巢”的动作，不正和上面描述的算法是一样的吗？

只是我们的算法还更加可爱一点，被推出去的鸟蛋，也就是被踢出去的元素，会放到另外一个位置上去。

我查阅资料的时候，当我知道布谷鸟就是杜鹃鸟的时候我都震惊了。

好多诗句里面都有杜鹃啊，比如我很喜欢的，唐代诗人李商隐的《锦瑟》：

锦瑟无端五十弦，一弦一柱思华年。
庄生晓梦迷蝴蝶，望帝春心托杜鹃。
沧海月明珠有泪，蓝田日暖玉生烟。
此情可待成追忆，只是当时已惘然。

自古以来。对于这诗到底是在说“悼亡”还是“自伤”的争论就没停止过。

但是这重要吗？

对我来说这不重要。

重要的是，在适当的时机，适当的气氛下，回忆起过去的事情的时候能适当的来上一句：“此情可待成追忆，只是当时已惘然”。

而不是说：哎，现在想起来，很多事情没有好好珍惜，真TM后悔。

哦，对了。

写文章的时候我还发现了一件事情。

布隆过滤器是 1970 年，一个叫做 Burton Howard Bloom 的大佬提出来的东西。

我写这些东西的时候，就想看看大佬到底长什么样子。

但是神奇的事情发生了，我前前后后，花了几天，墙内墙外翻了个底朝天，居然没有找到大佬的任何一张照片。

我的寻找，止步于发现了这个网站：

https://www.quora.com/Where-can-one-find-a-photo-and-biographical-details-for-Burton-Howard-Bloom-inventor-of-the-Bloom-filter

这个问题应该是在 9 年前就被人问出来了，也就是 2012 年的时候：

确实是在网上没有找到关于 Burton Howard Bloom 的照片。

真是一个神奇又低调的大佬。

有可能是一个倾国倾城的美男子吧。

最后说一句（求关注）

好了，看到了这里安排个“一键三连”（转发、在看、点赞）吧，周更很累的，不要白嫖我，需要一点正反馈。

才疏学浅，难免会有纰漏，如果你发现了错误的地方，可以在后台提出来，我对其加以修改。

感谢您的阅读，我坚持原创，十分欢迎并感谢您的关注。

往期推荐