爱因斯坦和高中几何问题
日期:2020年09月02日
正文共:3641字6图
预计阅读时间:10分钟
来源:算数君

一个令人费解的回复
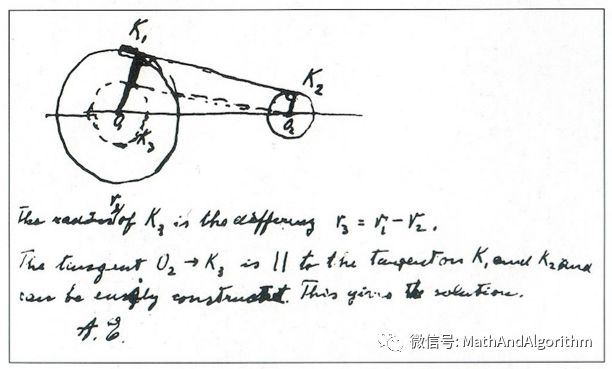
图片中几何示意图下的手写说明为:


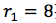 英寸,
英寸,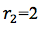 英寸,所以虚线圆
英寸,所以虚线圆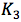 的半径6英寸。
的半径6英寸。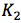 的圆心
的圆心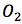 画出一条到虚线圆
画出一条到虚线圆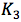 的切线。圆垂直于切线的半径也必然是虚线圆
的切线。圆垂直于切线的半径也必然是虚线圆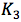 的半径。因此,可以使用尺规构建圆心
的半径。因此,可以使用尺规构建圆心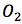 到
到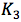 的切线,这条切线必然是等距的,也即平行于圆
的切线,这条切线必然是等距的,也即平行于圆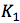 和
和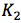 的外切线。爱因斯坦使用虚线画出了这条切线。更进一步,我们可以发现这条切线的长度就是我们所需要的问题中待求的长度。
的外切线。爱因斯坦使用虚线画出了这条切线。更进一步,我们可以发现这条切线的长度就是我们所需要的问题中待求的长度。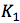 和
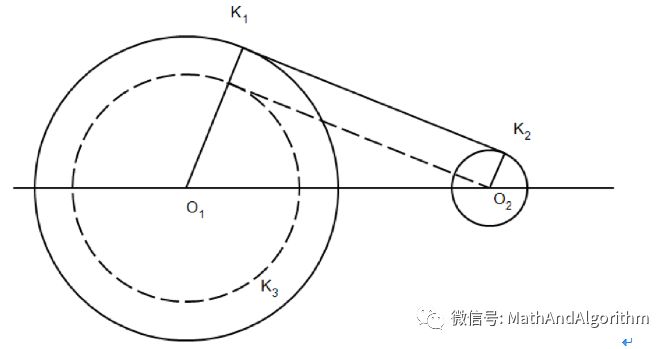
和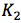 必须是相切的两个圆,即在某一个点上吻合。在图4中,我们给出了包含全部已知信息和爱因斯坦给出的构造方法的示意图。现在我们来看看这两个圆的情况。
必须是相切的两个圆,即在某一个点上吻合。在图4中,我们给出了包含全部已知信息和爱因斯坦给出的构造方法的示意图。现在我们来看看这两个圆的情况。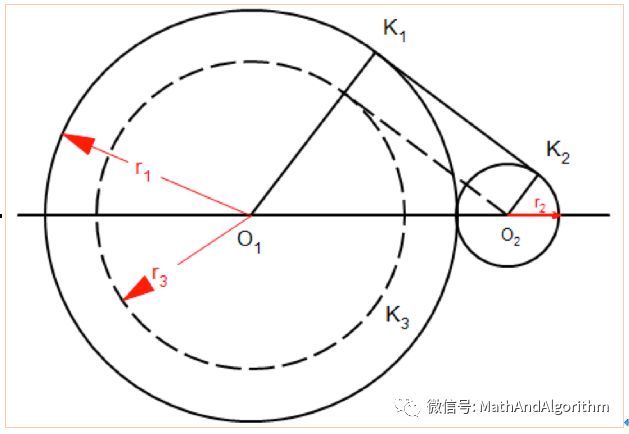
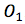 到
到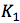 (结束于
(结束于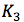 );
);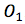 到
到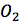 (直角三角形的斜边);爱因斯坦构造出的虚线。使用毕达哥拉斯定理求解这个直角三角形,那么需要的切线长度可以简化为
(直角三角形的斜边);爱因斯坦构造出的虚线。使用毕达哥拉斯定理求解这个直角三角形,那么需要的切线长度可以简化为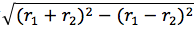 或
或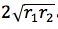 者。代入题目中所给出的数字,可知公共外切线的长度为8英寸。
者。代入题目中所给出的数字,可知公共外切线的长度为8英寸。后续媒体报道
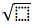 ,这就产生了无关的也没有意义数学等式。
,这就产生了无关的也没有意义数学等式。
— THE END —

评论
