冷淡的面试官,让我手写LRU缓存淘汰算法打发时间!

背景
在我们这个日益追求高效的世界,我们对任何事情的等待都显得十分的浮躁,网页页面刷新不出来,好烦,电脑打开运行程序慢,又是好烦!那怎么办,技术的产生不就是我们所服务么,今天我们就聊一聊缓存这个技术,并使用我们熟知的数据结构--用链表实现LRU缓存淘汰算法。
在学习如何使用链表实现LRU缓存淘汰算法前,我们先提出几个问题,大家好好思考下,问题如下:
什么是缓存,缓存的作用? 缓存的淘汰策略有哪些? 如何使用链表实现LRU缓存淘汰算法,有什么特点,如何优化?
好了,我们带着上面的问题来学进行下面的学习。
1、什么是缓存,缓存的作用是什么?
缓存可以简单的理解为保存数据的一个副本,以便于后续能够快速的进行访问。以计算机的使用场景为例,当cpu要访问内存中的一条数据时,它会先在缓存里查找,如果能够找到则直接使用,如果没找到,则需要去内存里查找;
同样的,在数据库的访问场景中,当项目系统需要查询数据库中的某条数据时,可以先让请求查询缓存,如果命中,就直接返回缓存的结果,如果没有命中,就查询数据库, 并将查询结果放入缓存,下次请求时查询缓存命中,直接返回结果,就不用再次查询数据库。
通过以上两个例子,我们发现无论在哪种场景下,都存在这样一个顺序:先缓存,后内存;先缓存,后数据库。但是缓存的存在也占用了一部分内存空间,所以缓存是典型的以空间换时间,牺牲数据的实时性,却满足计算机运行的高效性。
仔细想一下,我们日常开发中遇到缓存的例子还挺多的。
操作系统的缓存
减少与磁盘的交互
数据库缓存
减少对数据库的查询
Web服务器缓存
减少对应用服务器的请求
客户浏览器的缓存
减少对网站的访问
2、缓存有哪些淘汰策略?
缓存的本质是以空间换时间,那么缓存的容量大小肯定是有限的,当缓存被占满时,缓存中的那些数据应该被清理出去,那些数据应该被保留呢?这就需要缓存的淘汰策略来决定。
事实上,常用的缓存的淘汰策略有三种:先进先出算法(First in First out FIFO);淘汰一定时期内被访问次数最少的页面(Least Frequently Used LFU);淘汰最长时间未被使用的页面(Least Recently Used LRU)
这些算法在不同层次的缓存上执行时具有不同的效率,需要结合具体的场景来选择。
2.1 FIFO算法
FIFO算法即先进先出算法,常采用队列实现。在缓存中,它的设计原则是:如果一个数据最先进入缓存中,则应该最早淘汰掉。
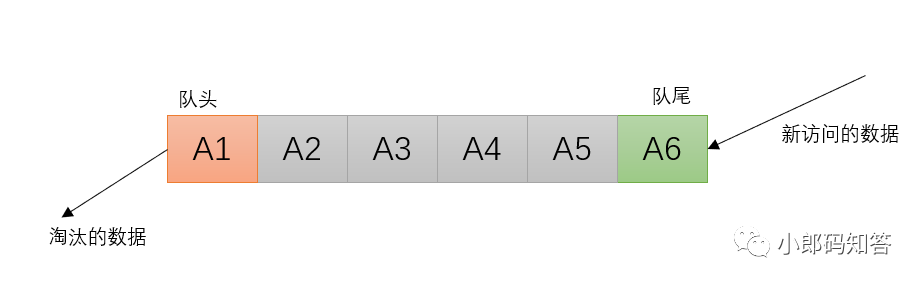
新访问的数据插入FIFO队列的尾部,队列中数据由队到队头按顺序顺序移动 队列满时,删除队头的数据
2.2 LRU算法
LRU算法是根据对数据的历史访问次数来进行淘汰数据的,通常使用链表来实现。在缓存中,它的设计原则是:如果数据最近被访问过,那么将来它被访问的几率也很高。
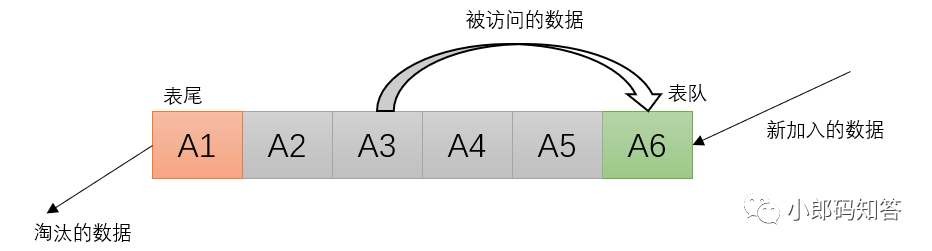
新加入的数据插入到链表的头部 每当缓存命中时(即缓存数据被访问),则将数据移到链表头部 当来链表已满的时候,将链表尾部的数据丢弃
2.3 LFU算法
LFU算法是根据数据的历史访问频率来淘汰数据,因此,LFU算法中的每个数据块都有一个引用计数,所有数据块按照引用计数排序,具有相同引用计数的数据块则按照时间排序。在缓存中,它的设计原则是:如果数据被访问多次,那么将来它的访问频率也会更高。
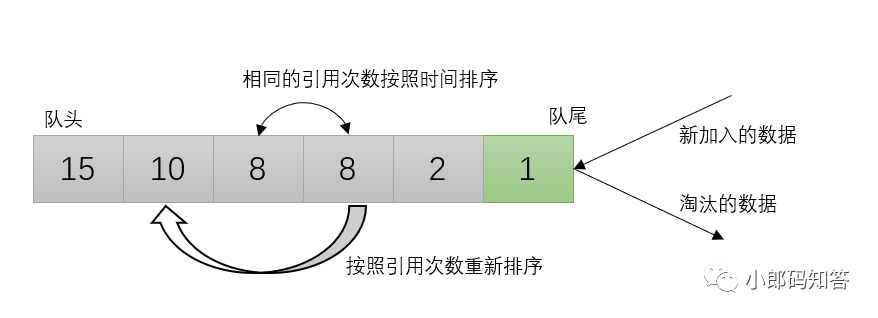
新加入数据插入到队列尾部(引用计数为1; 队列中的数据被访问后,引用计数增加,队列重新排序; 当需要淘汰数据时,将已经排序的列表最后的数据块删除。
3、如何使用链表实现缓存淘汰,有什么特点,如何优化?
在上面的文章中我们理解了缓存的概念及淘汰策略,其中LRU算法是笔试/面试中考察比较频繁的,我秋招的时候,很多公司都让我手写了这个算法,为了避免大家采坑,下面,我们就手写一个LRU缓存淘汰算法。
我们都知道链表的形式不止一种,我们应该选择哪一种呢?
思考三分钟........
好了,公布答案!
事实上,链表按照不同的连接结构可以划分为单链表、循环链表和双向链表。
单链表
每个节点只包含一个指针,即后继指针。 单链表有两个特殊的节点,即首节点和尾节点,用首节点地址表示整条链表,尾节点的后继指针指向空地址null。 性能特点:插入和删除节点的时间复杂度为O(1),查找的时间复杂度为O(n)。
循环链表
除了尾节点的后继指针指向首节点的地址外均与单链表一致。 适用于存储有循环特点的数据,比如约瑟夫问题。
双向链表
节点除了存储数据外,还有两个指针分别指向前一个节点地址(前驱指针prev)和下一个节点地址(后继指针next)
首节点的前驱指针prev和尾节点的后继指针均指向空地址。
双向链表相较于单链表的一大优势在于:找到前驱节点的时间复杂度为O(1),而单链表只能从头节点慢慢往下找,所以仍然是O(n).而且,对于插入和删除也是有优化的。
我们可能会有问题:单链表的插入删除不是O(1)吗?
是的,但是一般情况下,我们想要进行插入删除操作,很多时候还是得先进行查找,再插入或者删除,可见其实是先O(n),再O(1)。
不熟悉链表解题的同学可以先看看我的上一篇算法解析文章刷了LeetCode链表专题,我发现了一个秘密。
因为我们需要删除操作,删除一个节点不仅要得到该节点本身的指针,也需要操作其它前驱节点的指针,而双向链表能够直接找到前驱,保证了操作时间复杂度为O(1),因此使用双向链表作为实现LRU缓存淘汰算法的结构会更高效。
算法思路
维护一个双向链表,保存所有缓存的值,并且最老的值放在链表最后面。
当访问的值在链表中时:将找到链表中值将其删除,并重新在链表头添加该值(保证链表中 数值的顺序是从新到旧) 当访问的值不在链表中时:当链表已满:删除链表最后一个值,将要添加的值放在链表头 当链表未满:直接在链表头添加
3.1 LRU缓存淘汰算法
极客时间王争的《数据结构与算法之美》给出了一个使用有序单链表实现LRU缓存淘汰算法,代码如下:
public class LRUBaseLinkedList<T> {
/**
* 默认链表容量
*/
private final static Integer DEFAULT_CAPACITY = 10;
/**
* 头结点
*/
private SNode<T> headNode;
/**
* 链表长度
*/
private Integer length;
/**
* 链表容量
*/
private Integer capacity;
public LRUBaseLinkedList() {
this.headNode = new SNode<>();
this.capacity = DEFAULT_CAPACITY;
this.length = 0;
}
public LRUBaseLinkedList(Integer capacity) {
this.headNode = new SNode<>();
this.capacity = capacity;
this.length = 0;
}
public void add(T data) {
SNode preNode = findPreNode(data);
// 链表中存在,删除原数据,再插入到链表的头部
if (preNode != null) {
deleteElemOptim(preNode);
intsertElemAtBegin(data);
} else {
if (length >= this.capacity) {
//删除尾结点
deleteElemAtEnd();
}
intsertElemAtBegin(data);
}
}
/**
* 删除preNode结点下一个元素
*
* @param preNode
*/
private void deleteElemOptim(SNode preNode) {
SNode temp = preNode.getNext();
preNode.setNext(temp.getNext());
temp = null;
length--;
}
/**
* 链表头部插入节点
*
* @param data
*/
private void intsertElemAtBegin(T data) {
SNode next = headNode.getNext();
headNode.setNext(new SNode(data, next));
length++;
}
/**
* 获取查找到元素的前一个结点
*
* @param data
* @return
*/
private SNode findPreNode(T data) {
SNode node = headNode;
while (node.getNext() != null) {
if (data.equals(node.getNext().getElement())) {
return node;
}
node = node.getNext();
}
return null;
}
/**
* 删除尾结点
*/
private void deleteElemAtEnd() {
SNode ptr = headNode;
// 空链表直接返回
if (ptr.getNext() == null) {
return;
}
// 倒数第二个结点
while (ptr.getNext().getNext() != null) {
ptr = ptr.getNext();
}
SNode tmp = ptr.getNext();
ptr.setNext(null);
tmp = null;
length--;
}
private void printAll() {
SNode node = headNode.getNext();
while (node != null) {
System.out.print(node.getElement() + ",");
node = node.getNext();
}
System.out.println();
}
public class SNode<T> {
private T element;
private SNode next;
public SNode(T element) {
this.element = element;
}
public SNode(T element, SNode next) {
this.element = element;
this.next = next;
}
public SNode() {
this.next = null;
}
public T getElement() {
return element;
}
public void setElement(T element) {
this.element = element;
}
public SNode getNext() {
return next;
}
public void setNext(SNode next) {
this.next = next;
}
}
public static void main(String[] args) {
LRUBaseLinkedList list = new LRUBaseLinkedList();
Scanner sc = new Scanner(System.in);
while (true) {
list.add(sc.nextInt());
list.printAll();
}
}
}
这段代码不管缓存有没有满,都需要遍历一遍链表,所以这种基于链表的实现思路,缓存访问的时间复杂度为 O(n)。
3.2使用哈希表优化LRU
事实上,这个思路还可以继续优化,我们可以把单链表换成双向链表,并引入散列表。
双向链表支持查找前驱,保证操作的时间复杂度为O(1) 引入散列表记录每个数据的位置,将缓存访问的时间复杂度降到O(1)
哈希表查找较快,但是数据无固定的顺序;链表倒是有顺序之分。插入、删除较快,但是查找较慢。将它们结合,就可以形成一种新的数据结构--哈希链表(LinkedHashMap)
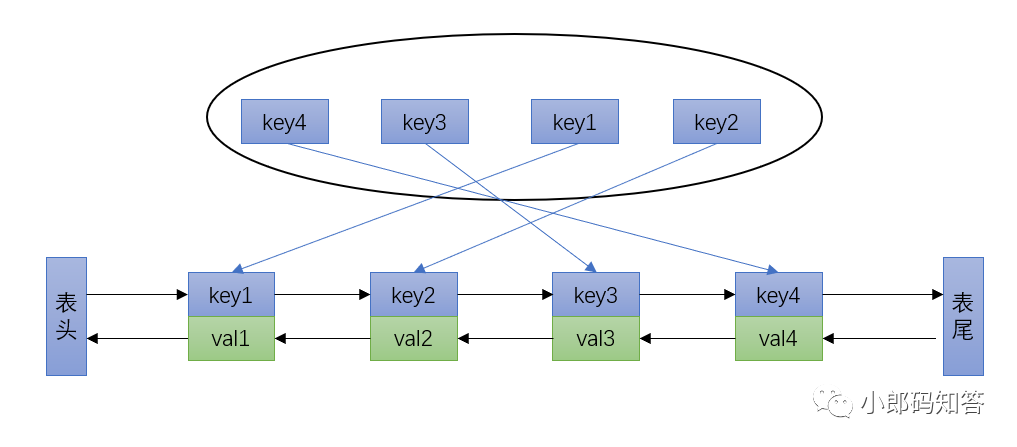
力扣上146题-LRU缓存机制刚好可以拿来练手,题图如下:
题目:
运用你所掌握的数据结构,设计和实现一个 LRU (最近最少使用) 缓存机制 。
实现 LRUCache 类:
LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
void put(int key, int value) 如果关键字已经存在,则变更其数据值;如果关键字不存在,则插入该组「关键字-值」。当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据值,从而为新的数据值留出空间。
思路:
我们的思路就是哈希表+双向链表
哈希表用于满足题目时间复杂度O(1)的要求,双向链表用于存储顺序 哈希表键值类型:<Integer, ListNode>,哈希表的键用于存储输入的key,哈希表的值用于存储双向链表的节点 双向链表的节点中除了value外还需要包含key,因为在删除最久未使用的数据时,需要通过链表来定位hashmap中应当删除的键值对 一些操作:双向链表中,在后面的节点表示被最近访问
新加入的节点放在链表末尾,addNodeToLast(node) 若容量达到上限,去除最久未使用的数据,removeNode(head.next) 若数据新被访问过,比如被get了或被put了新值,把该节点挪到链表末尾,moveNodeToLast(node)
为了操作的方便,在双向链表头和尾分别定义一个head和tail节点。
代码
class LRUCache {
private int capacity;
private HashMap<Integer, ListNode> hashmap;
private ListNode head;
private ListNode tail;
private class ListNode{
int key;
int val;
ListNode prev;
ListNode next;
public ListNode(){
}
public ListNode(int key, int val){
this.key = key;
this.val = val;
}
}
public LRUCache(int capacity) {
this.capacity = capacity;
hashmap = new HashMap<>();
head = new ListNode();
tail = new ListNode();
head.next = tail;
tail.prev = head;
}
private void removeNode(ListNode node){
node.prev.next = node.next;
node.next.prev = node.prev;
}
private void addNodeToLast(ListNode node){
node.prev = tail.prev;
node.prev.next = node;
node.next = tail;
tail.prev= node;
}
private void moveNodeToLast(ListNode node){
removeNode(node);
addNodeToLast(node);
}
public int get(int key) {
if(hashmap.containsKey(key)){
ListNode node = hashmap.get(key);
moveNodeToLast(node);
return node.val;
}else{
return -1;
}
}
public void put(int key, int value) {
if(hashmap.containsKey(key)){
ListNode node = hashmap.get(key);
node.val = value;
moveNodeToLast(node);
return;
}
if(hashmap.size() == capacity){
hashmap.remove(head.next.key);
removeNode(head.next);
}
ListNode node = new ListNode(key, value);
hashmap.put(key, node);
addNodeToLast(node);
}
}
巨人的肩旁:
[1]数据结构与算法之美-王争
[2]力扣-LRU缓存机制(146题)
[3]https://blog.csdn.net/yangpl_tale/article/details/44998423
[4]https://leetcode-cn.com/problems/lru-cache/solution/146-lru-huan-cun-ji-zhi-ha-xi-biao-shuan-l3um/
