【SU Ruby教程】图元定义(2)：端点、边线与平面类-技术圈

本篇介绍图元类的三巨头，即端点类（Vertex）、边线类（Edge）和平面类（Face）。可以毫不夸张地说，这三个类几乎就是 SketchUp 立体表现的全部内容。端点类是其中最简单的空间概念，边线就是两个端点的连线，平面就是几个边线所包围的形体。所谓“一生二，二生三，三生万物”，至此之后 SketchUp 中凡此种种各种图元与相关概念都是由它们组合派生而来，或者服务于它们。

图元定义(2)：端点、边线与平面类

【本期目录】

（1）端点类 Vertex

①端点不是图元

②从端点到图元

（3）平面类 Face

①平面的一般创建方法

②平面的特殊创建方法

③平面的属性

④平面中的边线与端点

（2）边线类 Edge

①边线的创建

②边线的空间属性

③边线的编辑

（1）端点类

①端点不是图元

首先需要说明，这三类并非都是图元。上一篇中有一张 Sketchup Ruby API 中实体类的继承关系图，从图中可以得知平面类（Face）和边线类（Edge）继承自图元类（Drawingelement），而端点类（Vertex）则和图元类在同一级，继承自实体类（Entity）。

因此边线和平面是图元，而端点不是图元。端点与另两类其实并不难区分，回想一下，选择工具可以选择边线也可以选择平面，却不能选择端点——这就足可见端点与它们的区别了。

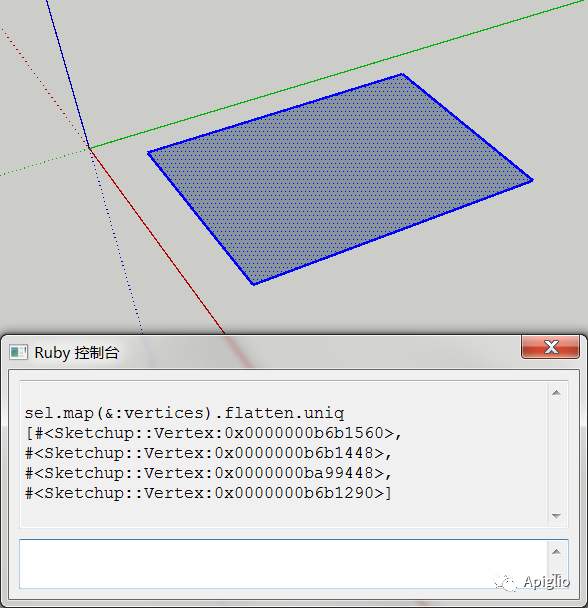
具体来说，端点类的创建和删除不由用户确定，它是根据边线和平面的存在而存在的。如果一个端点仅参与构成一个边线，当边线被删除时，端点就会一并删除；而如果一个边线仅参与构成一个平面，当平面被删除时，边线依然存在。


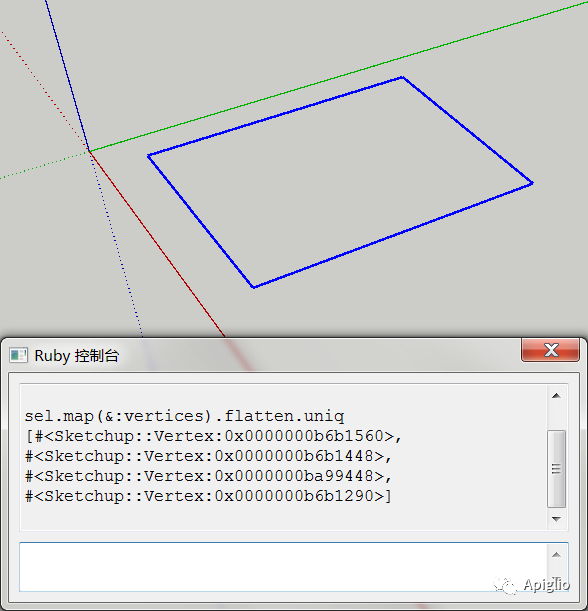
平面及其边线	删除平面

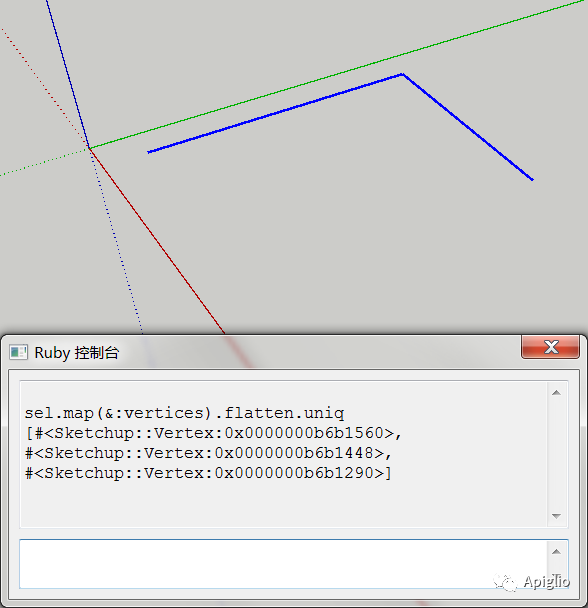
删除对位的两段边线	删除邻位的两段边线

以上图片中使用如下的代码来查看选中的所有图元包含的端点，这使用了 Edge 类和 Face 类的 .vertices 方法：

sel=Sketchup.active_model.selectionp sel.map{|ent|ent.vertices}.flatten.uniq

此方法可以返回一个包含边线或平面图元所有端点的数组。每一个边线都会返回起讫点，而平面图元则会按照一个方向返回所有顶点。由于端点存在共用现象，所以最后需要使用 .uniq 方法排除重复。

但是以上方法仅能用在选区内只有边线和平面的情况，因为其他图元都没有 .vertices 方法。如果选区中有其他类型图元时需要改成以下形式：

sel=Sketchup.active_model.selectionp sel.select{|i|i.respond_to? :vertices}.map(&:vertices).flatten.uniq

可以通过 .respond_to? 方法判断一个实例是否有 .vertices 方法，进行预先的筛选。在 SU 中有以下几类实例有此方法，但其中属于图元的只有边线和平面两类，另外的 Curve、 ArcCurve 和 Loop 三类都是辅助图元而存在的概念，分别按顺序记录一组边线，而并非图元。而 SandboxTools:: Terrain 不在教程讨论范围内。

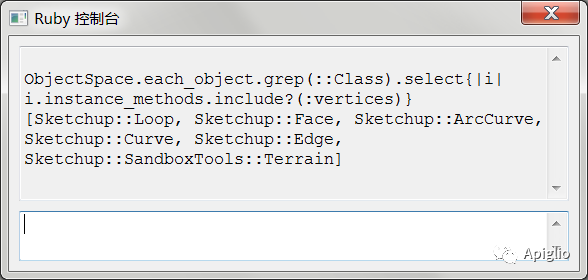
通过 .vertices 方法获得的 Vertex 类实例，可以通过 .position 方法获得端点的位置，而其返回值就是教程第六篇 [SU-R06] 中介绍的 Geom:: Point3d 类实例。

ents=Sketchup.active_model.entitiesputs ents.grep(Sketchup::Face)[0].vertices.map(&:position)#>> (1889.984682mm, 4997.647474mm, 0mm)#>> (4012.984682mm, 4997.647474mm, 0mm)#>> (4012.984682mm, 2487.647474mm, 0mm)#>> (1889.984682mm, 2487.647474mm, 0mm)

②从端点到图元

端点虽然不是图元，但是它与之后的两类图元密不可分，在已知一个端点的情况下可以通过 Vertex 类的方法取得与之相连的边线或平面图元。

为了下文更好地展示图形之间的关系，先进行一些测试前的配置，首先创建一个矩形平面，分别用全局变量引用平面及其四个边线图元：

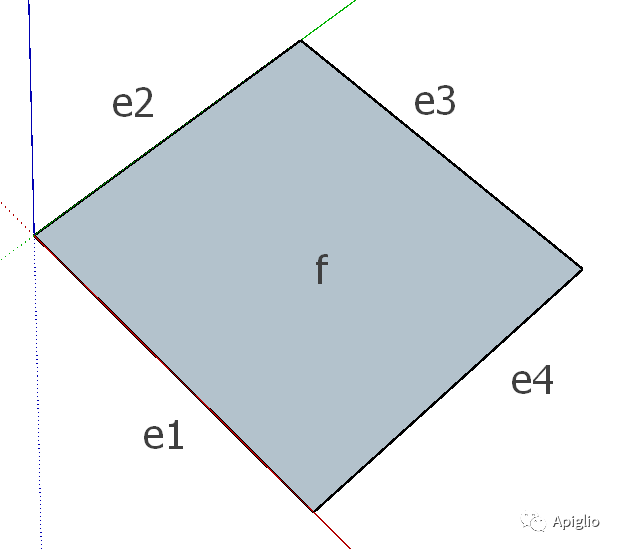用不同名称的全局变量引用每一个图元。使用以下代码，配合选区工具完成：

sel=Sketchup. active_model. selection

$f=sel[0]

注：此处使用全局变量为下文 iden 函数提供方便，否则应极力避免使用全局变量。

之后定义一个 iden 函数，用于返回代表图元的符号：

# 定义一个显示图元编号的方法def iden(ent)  if ent==$f then return "f" end  if ent==$e1 then return "e1" end  if ent==$e2 then return "e2" end  if ent==$e3 then return "e3" end  if ent==$e4 then return "e4" end  return nilend

这样在给定一个图元实例时，只需要使用这个函数就能得知这个图元在上图中对应的符号是哪个了：

e2.vertices[0].edges.map{|i|iden(i)}#>> ["e2", "e3"]e2.vertices[1].edges.map{|i|iden(i)}#>> ["e2", "e1"]
e2.faces.map{|i|iden(i)}#>> ["f"]e4.faces.map{|i|iden(i)}#>> ["f"]
e2.vertices[1].used_by? e3#>> falsee2.vertices[1].used_by? e1#>> truee2.vertices[1].used_by? f#>> true
iden(e2.vertices[1].common_edge e2.vertices[0])#>> e2iden(e2.vertices[1].common_edge e1.vertices[1])#>> e1iden(e2.vertices[1].common_edge e4.vertices[1])#>> (nil)

以上代码中， .edges 和 .faces 方法显然是返回包含了所有使用该端点的边线和平面的数组。需要注意 .faces 方法有可能返回空数组 []，而正常情况下 .edges 方法是一定会返回非空数组的。

.used_by? 方法判断端点是否被特定平面或边线使用，可以被理解为 .edges 和 .faces 方法的逆过程。以下自定义方法可以在效果上替代原方法：

module Sketchup  class Vertex    def used_by2?(de)      if de.is_a? Sketchup::Edge then        return self.edges.include?(de)      elsif de.is_a? Sketchup::Face then        return self.faces.include?(de)      else        raise ArgumentError.new("Edge or Face required")      end    end  endend

.common_edge 方法返回连接两个端点的边线图元，如果没有则返回 nil。需要注意，此方法不对不合理的参数负责：当使用此方法查找同一个点之间的共同边线，方法并不会报错，而是返回该点 .edges 结果的第一个边线图元。因此，以下自定义方法可以在效果上替代原方法：

module Sketchup  class Vertex    def common_edge2(de)      unless de.is_a? Sketchup::Vertex then        raise ArgumentError.new("expected Sketchup::Vertex")      end      return self.edges.find{|e|e.vertices.include?(de)}    end      endend

端点类另外还有 .curve_interior? 和 .loops 这两个方法，分别用来判断端点是否是曲线内的端点和返回需要该端点的环形结构。这两个方法涉及 Curve 类和 Loop 类，会在之后的教程中介绍。

（2）边线类

①边线的创建

边线类（Edge）属于图元类（Drawingelement），所以它可以由用户创建。创建边线类最一般的方法是使用 Entities 类的 .add_line 和 .add_edges 方法。前者返回一条边线图元，后者返回一个边线数组。

ents=Sketchup.active_model.entitiesedg=ents.add_line [0,0,0],[100.mm,100.mm,0]p edg#>> #<Sketchup::Edge:0x0000000b8ab730>
es=ents.add_line [0,0,0],[100.mm,0,0],[100.mm,100.mm,0]p es#>> #<Sketchup::Edge:0x0000000baa8ec0>
edges=ents.add_edges [0,0,100.mm],[100.mm,0,100.mm],[100.mm,100.mm,100.mm]p edges#>> [#<Sketchup::Edge:0x0000000b9c8c30>, #>>  #<Sketchup::Edge:0x0000000b9c8c08>]
edge=ents.add_edges [0,0,100.mm],[100.mm,100.mm,100.mm]p edge#>> [#<Sketchup::Edge:0x0000000ba54a28>]

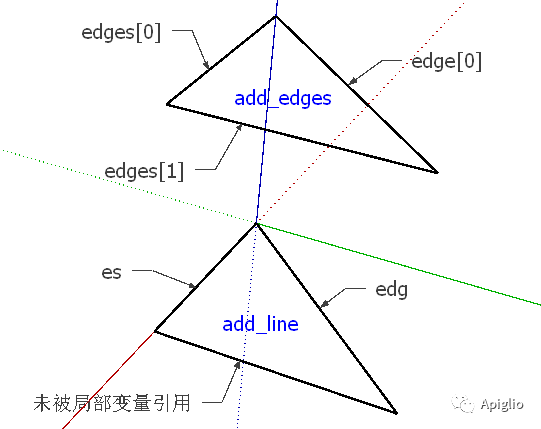
下图的六条边线由以上代码绘制，其中在基平面上的三角形由 .add_line 绘制，其上的由 .add_edges 绘制。对于模型来说，两个三角形除了高度位置以外没有任何不同。

代码中使用了赋值符号，使得这些局部变量会存储方法返回的图元。如左图的文字标注所描述的，两个创建方法的返回结果略有不同。

②边线的空间属性

边线由两个端点连线而成，有起点和终点，分别用 .start 和 .end 方法返回， .vertices 方法返回的数组也总是起点在前终点在后。因此以下两行代码返回值总为 true：

ents.grep(Sketchup::Edge).all?{|i|i.start==i.vertices[0]}ents.grep(Sketchup::Edge).all?{|i|i.end==i.vertices[1]}

边线类同样有 .used_by? 方法，可以用于检验该边线是否与某个端点相连，使用方法与 Vertex 的同名方法相似，原理如下：

module Sketchup  class Edge    def used_by2?(de)      if de.is_a? Sketchup::Vertex then        return self.vertices.include?(de)      elsif de.is_a? Sketchup::Face then        return self.faces.include?(de)      else        return false      end    end   endend

另外还有 .other_vertex 方法在给定一个端点的情况下返回该边线的另一个端点。与 Vertex 类的 .common_edge 方法有些类似，此方法也不对不合理的参数负责：如果参数中的端点不在边线上，方法就会返回边线的起点，就像如下的代替实现方案一样：

module Sketchup  class Edge    def other_vertex2(de)      unless de.is_a? Sketchup::Vertex then        raise ArgumentError.new("expected Sketchup::Vertex")      end      return self.vertices.find{|e|e != de}    end      endend

除此之外，边线类还可以返回其自身所在的直线（ .line 方法）和长度（ .length 方法），由于前者在往期教程 [SU-R06] 中已详细说明，后者相对简单，故不再赘述。

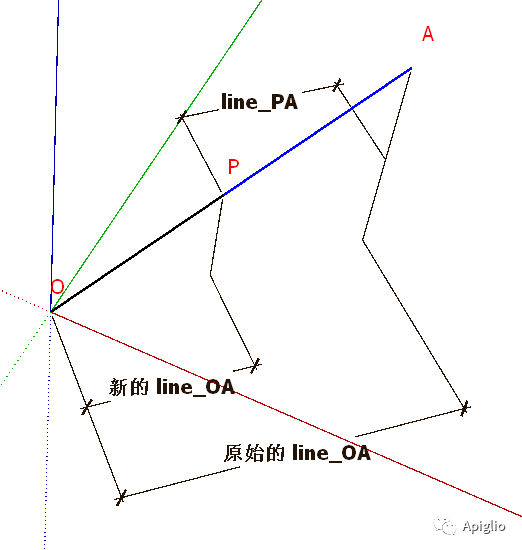
边线类还提供 .split 方法，用于在边线的某一个位置打断，使之成为两段边线。

line_OA = ents.add_line [0,0,0],[100.mm,100.mm,100.mm]pt_O = line_OA.startpt_A = line_OA.endline_PA = line_OA.split(0.5)# 0.5 表示等分pt_P = line_PA.startputs pt_P.position#>> (50mm, 50mm, 50mm)

以上代码新建一条边线 OA 后，在 OA 中点 P 处打断，产生新的边线 PA。而原先的 line_OA，虽然名称还是“OA”，实际上已经指向边线 OP。

打断的过程相当于将原线段的终点从 A 处改到断点处 P，之后再新建一条从断点 P 到 A 的边线。并且将新创建的这条边线图元作为 .split 方法的返回值。

旧边线打断后向量方向不变，新边线向量方向与之也相同。

更多地情况下， .split 方法会使用具体点位置作为参数，而不是如上述例子中那样使用线段长度的百分比。这个参数可以是 Geom:: Point3d 或者是能代表三维坐标的数组。

官方的文档中强调这个参数必须在边线上，因此在使用这种方式打断边线时，最好使用 Geom:: Point3d 或 Array 的 .on_line? 方法判断点是否在边线上：

If a Point3d is given, it must be a point that is on the Edge.
ruby.sketchup.com/Sketchup/Edge.html#split-instance_method

不过我的测试（SU2018和SU7）结果是只要参数点能投影在边线范围内，这个方法就能够正常运行，不会报错。

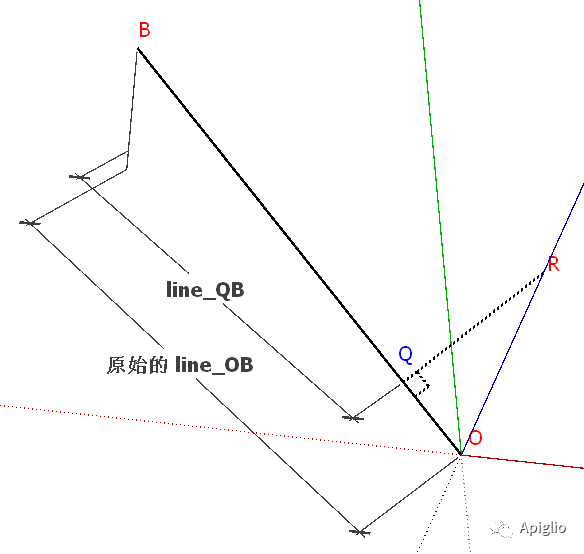
line_OB = ents.add_line [0,0,0],[-200.mm,200.mm,100.mm]pt_O = line_OB.startpt_B = line_OB.endpos_R = Geom::Point3d.new([0,0,150.mm])line_QB = line_OB.split(pos_R)pt_Q = line_QB.startputs pt_Q.position#>> (-33.333333mm, 33.333333mm, 16.666667mm)

以上代码中的 pos_R 并不在 line_OB 上，但是同样可以通过 R 来打断 OB，而断点 Q 可以有以下两种解释：

左图中的Q坐标可以通过以下两种方式获得：

①点到直线的投影

pos_Q = pos_R. project_to_line( line_OB. line)

②过点垂直于直线的平面与直线的交点

pos_Q = Geom. intersect_line_plane( line_OB. line, [pos_R, line_OB. line[1]])

使用 .split 方法后，模型中会增加一个边线类。因此，也可以将此方法视为创建边线的特殊方法。

③边线的编辑

边线有两个与平面有关的属性——软化（Soft）和平滑（Smooth）。前者用于表示不规则形状的表面，后者用于规定平滑光照。如下图所示：

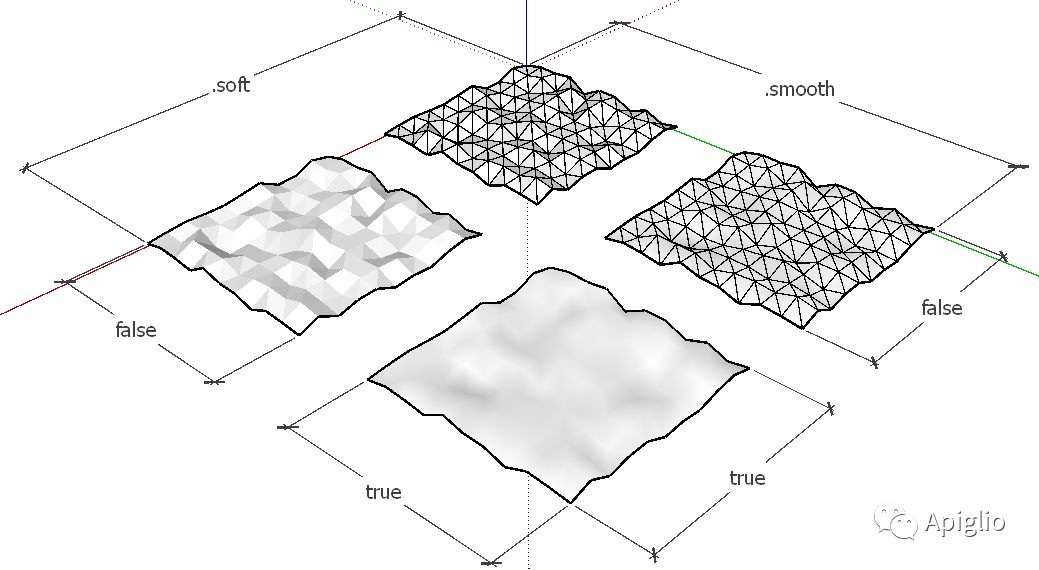
这两个属性可以直接通过图元信息窗口修改，当然自然也可以用代码实现。

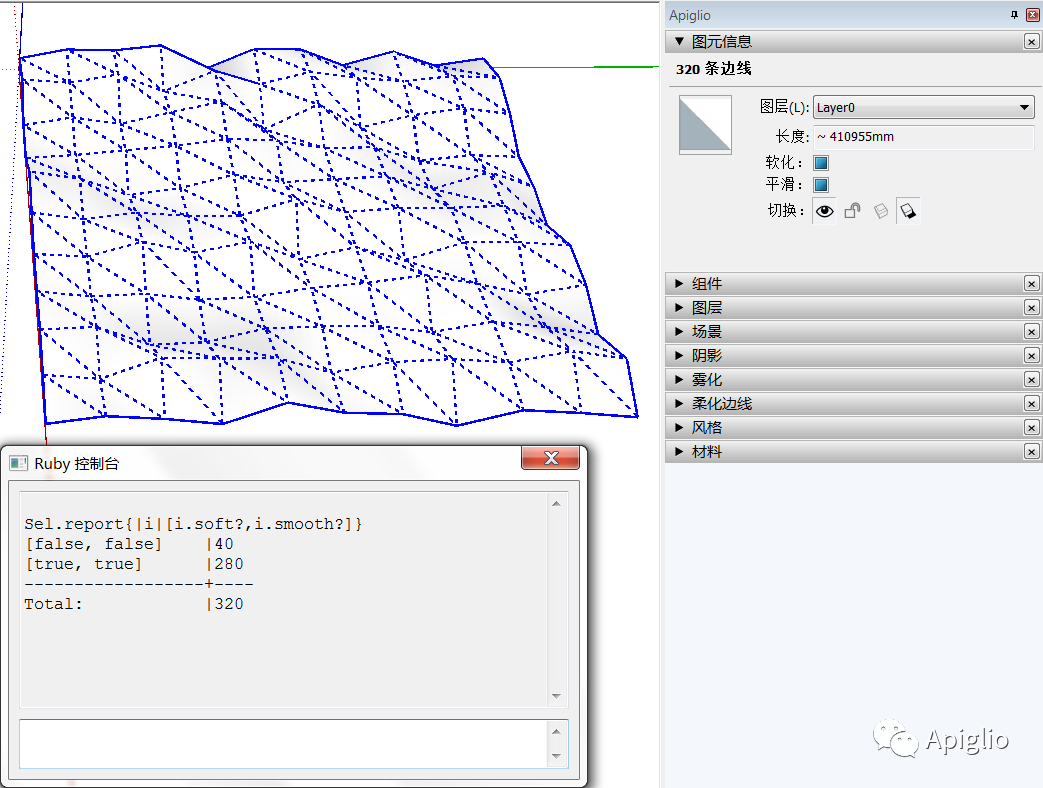
（图中 Sel.report 为自定义代码工具，详见 SU-2021-05）

类似于图元类的“hidden”和“visible”，“soft”和“smooth”同样使用问号和等号后缀的方法来进行读写（以下用 “soft” 举例）：

p ents.grep(Sketchup::Edge).any?{|i|i.soft?}#>> falseents.grep(Sketchup::Edge).each{|i|  i.soft=true}p ents.grep(Sketchup::Edge).all?{|i|i.soft?}#>> true

另外，边线类还有 .curve 属性和 .explode_curve 方法，两者与曲线定义有关，会在之后的篇幅中介绍。

（3）平面类

①平面的一般创建方法

平面类（Face）也属于图元类，所以它也可以由用户创建。创建边线类最一般的方法是使用 Entities 类的 .add_face 方法，此方法用于绘制单独一个平面。如果参数正确，成功绘制了平面，此方法返回这个平面图元的引用，否则返回 nil。

ents=Sketchup.active_model.entitiesf1=ents.add_face [0,0,0],[100.mm,0,0],[100.mm,100.mm,0],[0,100.mm,0]p f1#>> #<Sketchup::Face:0x0000000bb965f8>
f2=ents.add_face [[0,0,100.mm],[100.mm,0,100.mm],[100.mm,100.mm,100.mm],[0,100.mm,100.mm]]p f2#>> #<Sketchup::Face:0x0000000bbc8d28>

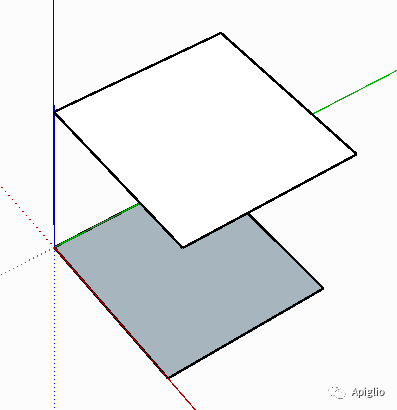
此方法与之前的出现过的多参数方法相同，都可以接受多个参数或是数组参数（请不要尝试这两种参数的杂糅形式，SU不会惯着你的）。执行以上代码后可以看到下图的效果， f1 和 f2 分别引用新创建的两个平面图元：

左图两个平面采用默认材质，可以发现两个平面的正反面方向不同，这是由给定参数和一些额外的规则确定的。具体的解释会在下一篇教程中展开。

作为参数的点坐标应该符合绘制平面的条件，否则就会报出以下错误：

#依次为“有重复点”、“点数量不足”和“点不成面”的参数错误f3=ents.add_face [[0,0,0],[50,50,0],[50,50,0],[0,0,0]]#>> Error: #<ArgumentError: Duplicate points in array>f4=ents.add_face [[0,0,0],[50,50,0]]#>> Error: #<ArgumentError: Not enough edges - at least 3 required>f5=ents.add_face [[0,0,100],[25,0,100],[50,0,100]]#>> Error: #<ArgumentError: Points are not planar>

另外， .add_face 方法同样也接受一组边线图元作为参数，要求边线数量至少为三，且能够首尾相连，与点坐标参数的使用方法类似，此处不额外举例。

除了 .add_face 方法， Entities 类中还有 .add_faces_from_mesh 方法也可以用于创建平面。这个方法可以一次性创建多个平面，但是需要使用 Geom:: PolygonMesh 这个类（这是 Geom 模块部分唯一还没有介绍的类，这部分内容会在之后补充）。

②平面的特殊创建方法

之前的两个创建平面的方法都需要有具体的坐标定义，并且都定义在 Entities 类之中。而平面类和边线类中，也定义有一些创建平面的方法。之所以称这些方法为“特殊的创建方法”，是因为它们与前者所需要的参数不同，需要在已有图元的基础上进一步创建平面。

首先是边线类（Edge）中提供有 .find_faces 方法，可以在图元容器中自己寻找此条边线可以参与创建的平面。这个方法在自动封面的工作中有不小的作用，不过在图元过于复杂时，效率比较低。

sels=Sketchup.active_model.selectionents=Sketchup.active_model.entitiescnt=0sels.each{|e|  cnt+=e.find_faces}puts cnt#>> 20

在选择下图左侧的线框之后，运行以上代码就可以得到右侧的成面效果：

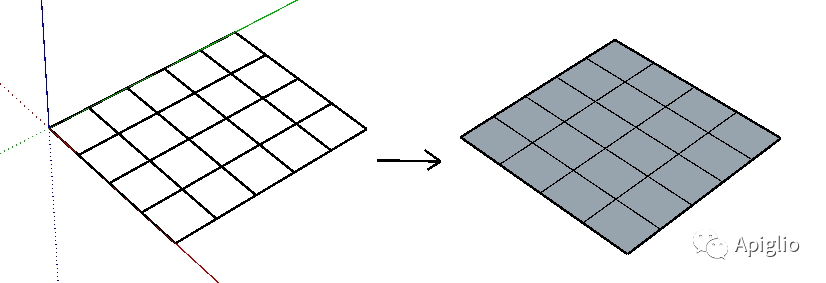
平面类（Face）本身也提供了两个可以进一步创建平面的方法，即 .pushpull 和 .followme 方法。这两个方法对应推拉工具和路径跟随工具，可以在平面所在的图元容器中，根据此平面的位置和参数的规定，创建由多个平面图元包围的几何形体。

这里简要的放两个例子用于自行测试：

(i) 推拉

#此例子来源于官方文档#ruby.sketchup.com/Sketchup/Face.html#pushpull-instance_methoddepth = 100width = 100model = Sketchup.active_modelentities = model.active_entitiespts = []pts[0] = [0, 0, 0]pts[1] = [width, 0, 0]pts[2] = [width, depth, 0]pts[3] = [0, depth, 0]# Add the face to the entities in the modelface = entities.add_face(pts)status = face.pushpull(100, true)

补充说明： .pushpull 方法的第一个参数表示推拉距离，其正方向为平面正面（默认材质的白色面）方向。第二个参数可以省略，省略时默认值为 false，表示不保留原始推拉平面（除非原先平面不构成立体图形）；此参数为 true 相当于使用推拉工具时按下 Ctrl 键。此方法不返回任何图元的引用，始终返回 nil。

(ii) 路径跟随

#此例子来源于官方文档，摘录时有改动#ruby.sketchup.com/Sketchup/Face.html#followme-instance_methodmodel = Sketchup.active_modelentities = model.active_entitiesdepth = 100width = 100points = [  Geom::Point3d.new(0, 0, 0),  Geom::Point3d.new(width, 0, 0),  Geom::Point3d.new(width, depth, 0),  Geom::Point3d.new(0, depth, 0)]face = entities.add_face(points)# Add the line which we will "follow" to the entities in the modelpoint1 = Geom::Point3d.new(0, 0, 0)point2 = Geom::Point3d.new(0, -10, 100)point3 = Geom::Point3d.new(0, -30, 200)point4 = Geom::Point3d.new(0, -60, 300)edges = entities.add_edges(point1, point2, point3, point4)face.followme(edges)

补充说明： .followme 方法可以接受一个或一组参数。参数必须是边线类。如果是一组边线，边线必须首尾相连（但是顺序没有要求）。此方法返回值为 false 或 true，表示是否成功创建图形。

执行以上两段代码后的效果：

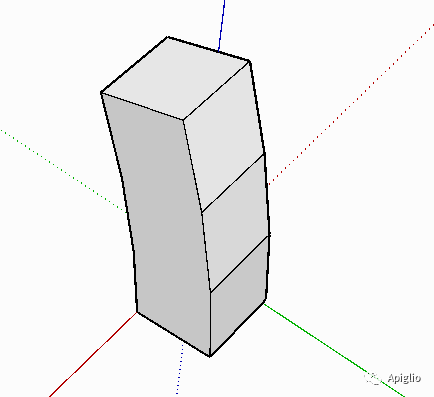③平面的属性

在之前的教程 [SU-R06] 中有提到过，平面图元可以通过 .plane 方法返回一个其所在的抽象平面，形式为一个长度为4的数组。类似地，还可以通过 .normal 方法返回平面的法线，其结果与 .plane[0..2] 是完全一样的。通过 .area 方法可以得到平面图元的面积：

f1.area#>> 15.500031000062002puts Sketchup.format_area(f1.area)#>> 10000 mm²# 第三行代码的返回结果根据当前模型的单位设置而定，# 此处当前模型单位设置为毫米，因此为毫米单位

平面图元可以将默认材质的白色面翻转，这一步可以通过鼠标右键菜单操作，也可以通过 .reverse! 方法实现。翻转前后， .plane 和 .normal 方法的返回值相反，相同参数的 .pushpull 方法产生的结果也相反。

平面图元还提供 .classify_point 方法用于判断一个点与平面图元的位置关系。此方法返回的是一个整数，将这个整数与平面类的类常数对比才能得知具体的位置关系。例如以下使用 Sketchup:: Face:: PointInside 常数表示点在面内的情况：

point_state = f.classify_point(pt)if point_state == Sketchup::Face::PointInside then  puts "pt在f平面内。"end

上述例子中 Sketchup:: Face:: PointInside 常数实际值为 1，但是需要特别注意的是：这个数字本身并不能代表特定含义，也不应该直接通过数字来判断点的状态。这是因为相同的点面关系的返回值在不同版本的 SU 中可能不一样：

puts Sketchup::Face.constants.map{|str|  str.to_s+"=#{eval('Sketchup::Face::'+str.to_s)}"}# 以下是 SU 7 的结果         是否有效#>> PointNotOnPlane=16      $ O#>> PointInside=1           $ O#>> PointOnVertex=4         $ X#>> PointUnknown=0          $ X#>> PointOnEdge=2           $ X#>> PointOutside=8          $ O
# 以下是 SU 2018 的结果      是否有效#>> PointUnknown=0          $ X#>> PointInside=1           $ O#>> PointOnVertex=2         $ O#>> PointOnEdge=4           $ O#>> PointOnFace=8           $ X#>> PointOutside=16         $ O#>> PointNotOnPlane=32      $ O

以上的输出结果中，符号 $ 之后表示对应版本的 .classify_point 方法是否会返回该值。不同版本的差异较大，因此最好不要依赖于此方法来确定点面关系。如果确有需要可以绘制相应的图形测试。

这里列出 SU7 和 SU2018 两个版本的判断结果以供参考：

左图中 arr[2] 和 arr[3] 不在平面图元所在平面内（有投射阴影），其余点都在平面图元所在平面。

图中的红色立方体位置仅供参考，测试点并非在其几何中心。

测试点	SketchUp 7	SU 2018
arr[0]	0x01 Inside	0x01 Inside
arr[1]	0x08 Outside	0x10 Outside
arr[2]	0x10 NotOnPlane	0x20 NotOnPlane
arr[3]	0x10 NotOnPlane	0x20 NotOnPlane
arr[4]	0x08 Outside	0x02 OnVertex
arr[5]	0x08 Outside	0x04 OnEdge
arr[6]	0x08 Outside	0x10 Outside

④平面中的边线与端点

平面由边线包围而成，因此类似于 .vertices 方法，平面类可以用 .edges 方法得到构成它的边线轮廓数组。反过来，边线类也可以通过 .faces 方法返回参与构成的平面数组。在绘图区双击一个平面图元即选中其 .edges 方法返回的所有图元；而双击一个边线图元，则会选中其 .faces 方法返回的所有图元。

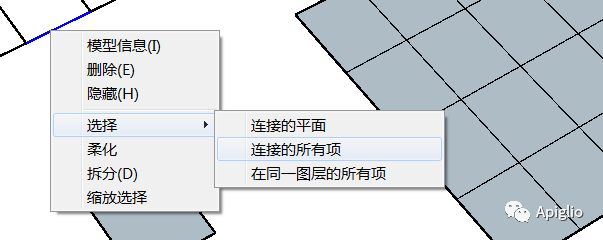
如果通过这两个方法连续交替地查询相连的平面和边线图元，直到找不到新的图元，那么就相当于在操作界面鼠标连续左击三次的“选择连接的所有项”功能，此功能便是 .all_connected 方法，边线类和平面类都能够使用。

边线类的 .used_by? 方法除了可以用来判断是否连接某端点以外，同样也可以用来判断是否连接某个平面， e.used_by? (f) 相当于 e.faces. include? (f)。类似于端点类的 .common_edge 方法，边线类也有 .common_face 方法，原理相同，此处不额外举例。

平面类还有 .mesh、 .loops 和 .outer_loop 方法，第一个与 Geom:: PolygonMesh 有关，后两个则与 Sketchup:: Loop 有关，这个在下一篇教程中就会涉及。

最后放一些与本次教程相关的代码。

# 此方法可以在测试点面关系数值时使用# 这样Face#classify_point的返回值就可以通过# 此方法转译成字符串输出在控制台def int2pointclass(i)  Sketchup::Face.constants.each{|str|    if eval('Sketchup::Face::'+str.to_s)==i then      return str.to_s    end  }  return "Unexpected"end
# 对于仅供临时使用的、不需要考虑版本迁移的代码而言# 或许可以使用点面状态的数值。# 例如，在SU2018中， # PointOnVertex = 0x02# PointOnEdge = 0x04# 0x02 | 0x04 == 0x06# 那么如果需要判断点在面的边缘就可以用以下表达：point_state = f.classify_point(pt)if point_state & 0x06 != 0 then  puts "pt在f平面的边缘"end

（完）

本文编号：SU-R11