Tester Program

Description

Tester Program

For this contest, we first designed the following problem (note that you do not have to solve it!):

Another Wall in the Maze

In ACM/ICPC contests, you'll often see questions such as "find the shortest path out of this maze." Let's turn this on its head and ask "given a path, find a maze for which the given path is the shortest path." Our paths will run vertically and horizontally between the regularly spaced points of a rectangular grid. The problem is to compute a set of unit-length baffles (walls) separating grid points that forces the given path to be the unique shortest path from its starting point to the end point. To make things more interesting, we will require that there should be no redundant walls constructed in the sense that it should not be possible to remove any wall and still have the given path as the unique shortest path. In the following figure for example, consider the path through the 8 ? 5 grid on the left maze of the top row. The wall placements in the two mazes to its right (top row) make that path unique. The two mazes on the lower row are faulty.
The path is not unique in the one on the left, and there are some redundant walls on the right.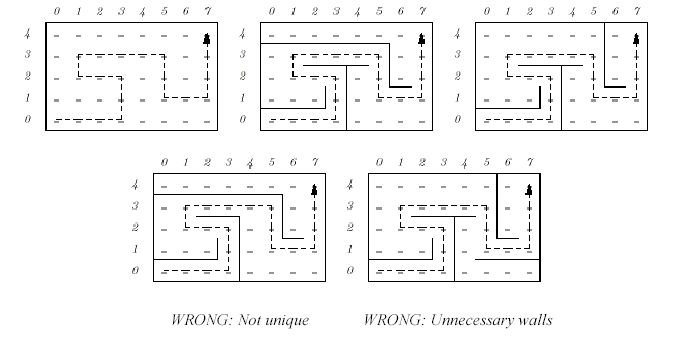

Input (of the original problem)

The first line of the input file contains a single integer t (1 ≤ t ≤ 10), the number of test cases, followed by the input data for each test case. The first line of each test case consists of two integers W and H (1 ≤ W, H ≤ 100) giving the width and height of the grid respectively. The second line of the test case contains a path. The path always starts in the lowerleft corner, (0, 0). It is specified as a string of U (up), D (down), L (left), and R (right) characters (with no embedded white space). You may assume that the path remains within the bounds of the maze and does not intersect itself. It may end anywhere in the maze (i.e., not necessarily in a corner or against a wall).

Output (of the original problem)

First line of the output for the i-th test case (starting from one) should contain an integer M, the number of walls used in the solution. Following the first line, there are M lines each containing a wall specification in the form of four consecutive integers corresponding to two pairs of (x, y) coordinates specifying adjacent grid points separated by the wall (0 ≤ x < W and 0 ≤ y < H). Note that the possible output is not unique. There should no blank line in the output.

Sample Input (of the original problem)

2
8 5
RRRUULLURRRRDDRRUUU
4 3
RRRUU

Sample Output (of the original problem)

19
0 0 0 1
1 0 1 1
2 0 2 1
2 1 3 1
3 0 4 0
3 1 4 1
3 2 4 2
3 2 3 3
2 2 2 3
4 2 4 3
0 3 0 4
1 3 1 4
2 3 2 4
3 3 3 4
4 3 4 4
5 3 5 4
5 3 6 3
5 2 6 2
6 1 6 2
2
2 2 3 2
2 2 2 1
This is the end of the original problem statement! Being lazy, we did not want to spend time to write a tester program for this problem, and decided to have you write this for us!
Write a program that receives both input and output as one input test case, and write as output CORRECT or INCORRECT to indicate whether or not the output is correct.

Input

You read both input and output of the original problem from the standard input;it has each output just after each case's input of the original problem.
Note that the output of original does not have formatting problems, i.e.,
The number of lines in the output file is correct and is as supposed to be.
There are no leading or trailing white space characters in output lines.
Wall specifications are correct, meaning that the four numbers correctly specify a possible wall within the boundary of the maze.

Output

Your program should write a single line for each test case of the input containing a single word CORRECT or INCORRECT, indicating the original problem has correctly produced the output for that test case or not.

Sample Input

2
8 5
RRRUULLURRRRDDRRUUU
19
0 0 0 1
1 0 1 1
2 0 2 1
2 1 3 1
3 0 4 0
3 1 4 1
3 2 4 2
3 2 3 3
2 2 2 3
4 2 4 3
0 3 0 4
1 3 1 4
2 3 2 4
3 3 3 4
4 3 4 4
5 3 5 4
5 3 6 3
5 2 6 2
6 1 6 2
4 3
RRRUU
2
2 2 3 2
2 2 2 1

Sample Output

CORRECT
INCORRECT

测试程序

描述

测试程序

本次比赛，我们首先设计了以下问题(注意，你不必解决它!)

迷宫中的另一堵墙

在ACM/ICPC竞赛中，您经常会看到诸如“找到走出这个迷宫的最短路径”这样的问题。让我们把它反过来问，“给定一条路径，找到一个给定路径是最短路径的迷宫。”我们的路径将在一个矩形网格的规则间隔点之间垂直和水平运行。问题是要计算一组单位长度的挡板(墙)，这些挡板将网格点分隔开来，迫使给定路径成为从起点到终点的唯一最短路径。为了让事情变得更有趣，我们将要求不存在多余的墙，也就是说它不可能移除任何墙，并且给定的路径仍然是唯一的最短路径。以下图为例，考虑通过8 ?5网格在迷宫的左顶行。在其右侧的两个迷宫(顶部一行)的墙放置使这条路径独特。下面两排的迷宫有问题。

左边的路径不是唯一的，右边有一些多余的墙。

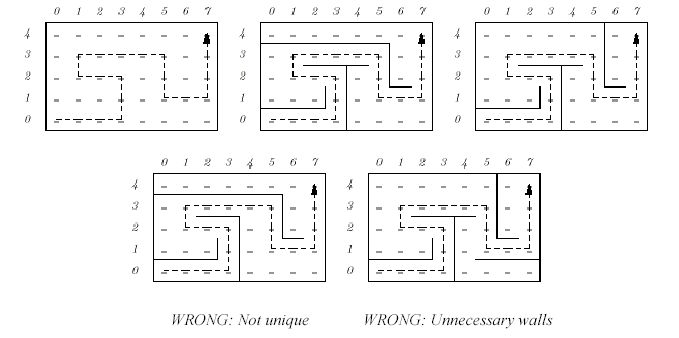
输入(原始问题)

输入文件的第一行包含单个整数t(1≤t≤10)，测试用例的数量，后面是每个测试用例的输入数据。每个测试用例的第一行由两个整数W和H(1≤W, H≤100)组成，分别给出网格的宽度和高度。测试用例的第二行包含一条路径。路径总是从左下角(0,0)开始。它被指定为一个由U(上)、D(下)、L(左)和R(右)字符组成的字符串(没有嵌入空格)。你可以假设这条路径仍然在迷宫的边界内，并且没有与自己相交。它可能在迷宫的任何地方结束(也就是说，不一定在一个角落或靠在墙上)。

(原始问题的)输出

第i个测试用例的输出的第一行(从第一行开始)应该包含一个整数M，即解决方案中使用的墙的数量。第一行后,有M行包含一个墙规范形式的四个连续整数对应两对(x, y)坐标指定相邻网格点隔着墙(0≤x < W和0≤y < H)。注意可能的输出不是独一无二的。输出中不应该有空行。

样本输入(原始问题的)

2
8 5
RRRUULLURRRRDDRRUUU
4 3
RRRUU

Sample Output (of the original problem)

19
0 0 0 1
1 0 1 1
2 0 2 1
2 1 3 1
3 0 4 0
3 1 4 1
3 2 4 2
3 2 3 3
2 2 2 3
4 2 4 3
0 3 0 4
1 3 1 4
2 3 2 4
3 3 3 4
4 3 4 4
5 3 5 4
5 3 6 3
5 2 6 2
6 1 6 2
2
2 2 3 2
2 2 2 1

这是最初的问题陈述的结束!由于懒惰，我们不想花时间为这个问题编写测试程序，所以决定让您为我们编写这个程序!

编写一个程序，将输入和输出都作为一个输入测试用例接收，并将其作为输出写入CORRECT或INCORRECT，以指示输出是否正确。

输入

您可以从标准输入中读取原始问题的输入和输出;它的每个输出刚好在每个case的原始问题输入之后。

注意，原始文件的输出没有格式问题，即:

输出文件中的行数是正确的，并且应该是正确的。

输出行中没有前导或尾随空白字符。

墙的规格是正确的，这意味着四个数字正确地指定了迷宫边界内可能的墙。

输出

您的程序应该为输入的每个测试用例编写一行代码，其中包含一个单词CORRECT或INCORRECT，表明原始问题是否正确地生成了该测试用例的输出。

Sample Input

2
8 5
RRRUULLURRRRDDRRUUU
19
0 0 0 1
1 0 1 1
2 0 2 1
2 1 3 1
3 0 4 0
3 1 4 1
3 2 4 2
3 2 3 3
2 2 2 3
4 2 4 3
0 3 0 4
1 3 1 4
2 3 2 4
3 3 3 4
4 3 4 4
5 3 5 4
5 3 6 3
5 2 6 2
6 1 6 2
4 3
RRRUU
2
2 2 3 2
2 2 2 1

Sample Output

CORRECT
INCORRECT

题意：

/**
* (1)求各点到源点的最小步数（DFS）
* (2)求各点到终点的最小步数（DFS）
* (3)如果点不是给定路径上的点，那么：该点到源点的最小步数＋该点到终点的最小步数<=给定路径的步数，否则给定路径不是唯一最短的
* (4)如果两相邻点a、b之间存在墙，那么：a到源点的最小步数＋1＋b到终点的最小步数<=给定路径的步数
*                               或者 a到终点的最小步数＋1＋b到源点的最小步数<=给定路径的步数，否则墙多余
* (5)如果存在点不可达，说明存在墙将该点封闭起来，可以证明墙至少有一块多余 （本程序未考虑这一点，也过了）*/

代码：

#include 
#include 
struct pos
{
int len[2];
int used;
int r;
int u;
}p[20][20];
int num, wallNum, w, h, Dx, Dy, minPath;
void DFS(int x, int y, int len, int flag)
{
if (len >= p[x][y].len[flag] && p[x][y].len[flag]!=0)
   return;
if (x+y!=0 && (x!=Dx||y!=Dy))
   p[x][y].len[flag] = len;
len++;
if (p[x][y].r==0 && x+1   DFS(x+1, y, len, flag);
if (p[x][y].u==0 && y+1   DFS(x, y+1, len, flag);
if (x-1>=0 && p[x-1][y].r==0)
   DFS(x-1, y, len, flag);
if (y-1>=0 && p[x][y-1].u==0)
   DFS(x, y-1, len, flag);
} 
int judge()
{
int i, j;
for (i=0; i   for (j=0; j   {
    if (p[i][j].used==0 && p[i][j].len[0]+p[i][j].len[1]<=minPath)
     return 0;
    if (p[i][j].r==1 && i+1minPath && p[i][j].len[1]+p[i+1][j].len[0]+1>minPath)
     return 0;
    if (p[i][j].u==1 && j+1minPath && p[i][j].len[1]+p[i][j+1].len[0]+1>minPath)
     return 0; 
   }
return 1;
}
int main()
{
int x, y, x1, y1, x2, y2;
char c;
scanf("%d", &num);
while (num--)
{ 
   memset(p, 0, sizeof(p));
   scanf("%d %d\n", &w, &h);
   p[0][0].used = 1;
   Dx = Dy = minPath = 0;
   while ((c=getchar())!='\n' && c!=EOF)
   {
    if (c == 'U')
     p[Dx][++Dy].used = 1;
    else if (c == 'D')
     p[Dx][--Dy].used = 1;
    else if (c == 'L')
     p[--Dx][Dy].used = 1;
    else if (c == 'R')
     p[++Dx][Dy].used = 1;
    minPath++;
   }
   scanf("%d", &wallNum);
   while (wallNum--)
   {
    scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
    x = x1 - x2;
    y = y1 - y2;
    if (x==0 && y==1)
     p[x2][y2].u = 1;
    else if (x==0 && y==-1)
     p[x1][y1].u = 1;
    else if (x==1 && y==0)
     p[x2][y2].r = 1;
    else if (x==-1 && y==0)
     p[x1][y1].r = 1;
   }
   DFS(0, 0, 0, 0);
   DFS(Dx, Dy, 0, 1); 
   if(judge())
    printf("CORRECT\n");
   else
    printf("INCORRECT\n");
}
return 0;
}