【技术分享】图遍历算法之广度优先遍历算法

广度优先遍历算法应用的是队列这种数据结构的特点，它的遍历过程如下：

（1）以图中的任一顶点V为出发点，首先访问顶点V。

（2）访问顶点V的所有未被访问过的邻接点V 1 ，V 2 ，……，V n 。

（3）按照V 1 ，V 2 ，……，V n 的次序，访问每个顶点的所有未被访问过的邻接点。

（4）以此类推，直到图中所有和顶点V连通的顶点都被访问过为止。

这里以下图所示的无向图为例来介绍此方法的遍历过程。

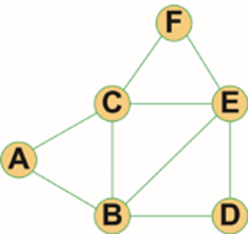
步骤1 ：假设以顶点A为起点，将顶点A放入队列，如下图所示。

步骤2 ：取出顶点A，将顶点A的邻接点B和C放入队列，如下图所示。

步骤3 ：根据队列“先进先出”的原则，取出顶点B，将与顶点B相邻并且未被访问过的顶点D和顶点E放入队列，如下图所示。

步骤4 ：取出顶点C，将与顶点C相邻并且未被访问过的顶点F放入队列，如下图所示。

步骤5 ：取出顶点D，将与顶点D相邻并且未被访问过的顶点放入队列。由于顶点D的邻接点B和E都已被访问过，所以无需放入队列中，如下图所示。

步骤6 ：取出顶点E，将与顶点E相邻并且未被访问过的顶点放入队列。由于顶点E的四个邻接点都已被访问过，所以无需放入队列中，如下图所示。

步骤7 ：取出顶点F，将与顶点F相邻并且未被访问过的顶点放入队列。由于顶点F的邻接点C和E都已被访问过，所以无需放入队列中，如下图所示。

此时，队列中的值都已被取出，表示图中的顶点都已被访问过。由此可知，本例中进行广度优先遍历的顺序为：顶点A、顶点B、顶点C、顶点D、顶点E、顶点F。

用Python代码描述上述过程，则算法代码如下：

def  bfs (graph, start):

    queue = [] #  定义队列

     queue.append(start) #  将起始顶点放入队列

     visited =  set () #  定义集合

     visited.add(start) #  将起始顶点放入已访问集合

     while  queue:

        vertex = queue.pop(0) #  取出队列第一个元素

         print (vertex, end  =  ' ' ) #  打印广度优先遍历的顶点

         for  w  in  graph[vertex] : #  遍历相邻的顶点

             if  w  not in  visited: #  如果该顶点未被访问过

                visited.add(w) #  将该顶点放入已访问集合

                 queue.append(w) #  把顶点放入队列