不要小瞧递归:它比大部分人想象中更强大
大数据文摘授权转载自数据实战派
作者:WhiteBlackGoose
译者:张雨佳
大部分人都知道递归的含义,即通过自身来定义一些东西。
但实际上,这种简单的定义可以完全改变你编写命令式算法的方式。无论你是使用Java、c#、Python还是F#的开发人员,都可以在通用编程语言中使用递归!
定义循环
首先介绍循环,循环不单单是“做n次同一件事”或“条件为真时进行重复”。我认为循环的迭代实际上是一个函数,它可以改变了某些全局变量的状态。并且循环是从某个初始状态开始的链式函数:循环是初始状态和转换(迭代)的有限链。
比如下面这个伪代码:
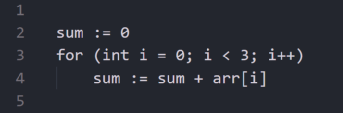
求和的常用递归方法
它的全局状态是元组“sum”和“i”,转换是在sum上对arr[i]求和并且令i + 1。
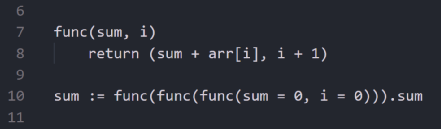
具有初始状态的链式转换
上面的代码中使用了三个“func”函数的嵌套,我们如何让这个链式函数自动运行呢?
事实上,我们可以教函数调用自己!
从循环到递归
下面我们让“func”函数调用自己。
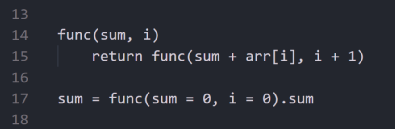
对数组所有元素求和的递归函数
你可能会发现,上面这个函数会无限次递归,所以我们需要添加循环的条件,类似于for或while函数的条件:
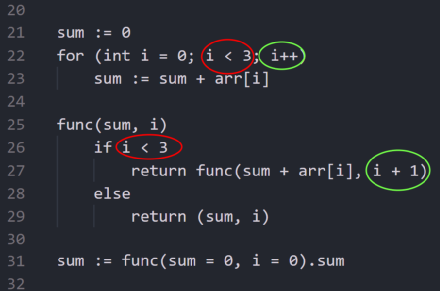
把循环转换成递归
可以看出,我们用递归操作定义了循环,而且这是一种尾递归,即直接将循环转换成递归(后面会进行详细解释)。
这同样也是一种归纳定义(inductive definition)。基础base是i大于等于3,转换函数是“假设func是为i + 1定义的,那么同样func函数也是为i定义的”。
递归的定义是如此简单,没有“改变”和变化的变量。它所做的只是返回一个或、】另一个东西,这难道不棒吗?
为什么需要递归?
因为递归更简单、更容易阅读、编写,也更容易调试。
方便阅读
举一个非常简单的例子:阶乘。下面是循环定义的阶乘操作:
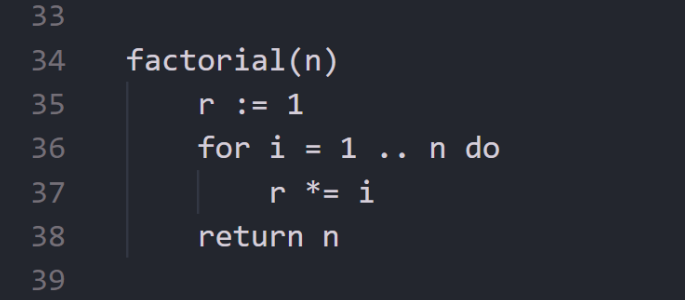
循环定义的阶乘
你能直接告诉我factorial(0)返回的值吗?factorial(4)的值是24吗?是比factorial(6)少一次迭代还是比factorial(120)多一次迭代呢?你需要知道1到n的循环中是否包含n,然后仔细建模。
那么阶乘的“模型”是什么?
其定义如下:
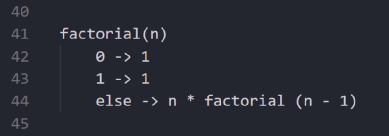
递归定义的阶乘
你不需要去想进行多少次迭代,只需要知道它在base下(0和1)是正确的,那么它在n转变到n-1时也会是正确的。
方便编写代码
我们再将目光转向斐波那契数列。在数学中,它的定义如下:

斐波那契数列的数学定义
但由于这样编写代码非常低效,所以没有人会这样写。
下面是一种命令式的编写方法:

斐波那契数列的循环定义
同样的,你能预测fib(5)的输出吗?你能确定应该返回的是a而不是b吗?你能确定有n次,n-1次还是n+1次迭代?
实际上,我们可以用递归方法写出相同时间复杂度的解决方案,也叫做memoization。在带有可以修改函数的修饰器(decorators)的语言中,我们只需要在上面添加一点操作:

memoization的斐波那契数列
这个函数对于相同的输入会返回相同的答案,并且时间复杂度是线性的,所以我们需要做的就是将其存入缓存。
(对于没有decorators的语言,你可以手动对输入进行检查,这并不难做到)
方便调试
与需要跳进函数的递归相比,似乎调试循环方法更容易一些,你只需要遍历迭代。
但事实上,调试递归定义的函数有两个优点:
(1)可以随时检查或计算任何输入下的函数值(但循环中不能任意选择迭代次数)。
(2)可以直观看到调用栈和每个栈帧中变量的值。
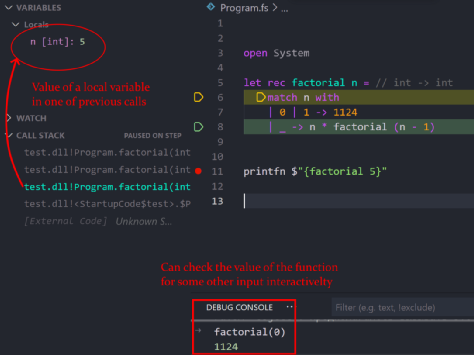
查看调用栈帧的变量。交互式地运行函数
递归还能干什么?
下面会展示一些递归的应用,但实际上,你可以将任何循环用递归实现。例如,可以遍历树结构:
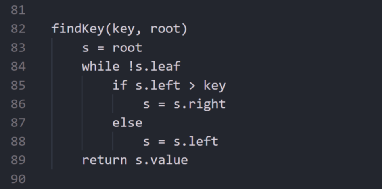
二叉查找树中查找对应值的循环方法
下面是等价的递归方法:
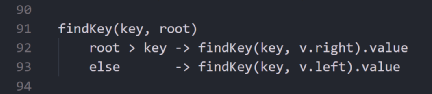
二叉查找树中查找对应值的递归方法
是不是看起来整洁许多!在复杂的算法中,阅读和编写这样的代码会比较容易,甚至都不需要进行调试。
那最主要的问题是,何时才会给出所需的答案?
下面是命令式代码:

命令式实现方法
首先为了进入循环,我们必须声明“n”并将其初值设置为空(null),并且每次都会检查重复条件“n是否等于null”,以确定输入的数字是否正确!
让我们简化这些繁杂的代码:

递归式实现方法
可见,递归方法更加直接明了。对上面代码的翻译是:
(1)输入数字
(2)读入数字
(3)如果数字为空,报告一个错误并再次输入
(4)否则,返回这个数字
现在,你同样可以翻译出之前的命令式循环方法了,它大概是这样的:
(1)假设数字为空
(2)当数字为空时,请求输入一个数字
(3)将读入的值分配给数字
(4)如果数字为空,则报告错误
(5)返回步骤2,重新开始
(6)返回数字
其他东西可以递归吗?
不仅可以用递归定义函数。我认为世界上所有的东西都可以用递归的方式定义,比如下面几个实际的例子。首先可以递归定义的东西是类型(types)。
类型的递归
二叉树节点是最简单的例子。二叉树的节点通常有0、1或2个子节点,并且节点的类型相同。
在函数式或函数式优先的语言中,有种叫做列表(list)的数据类型,相当于离散数学中的字符串。那么,列表满足以下特点:
(1)要么是空的
(2)要么存在第一个元素,且剩下部分也是列表类型
下面是列表的定义:
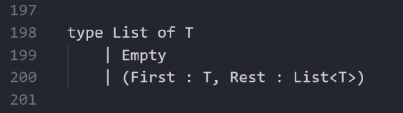
归纳法定义的列表
其中,T是通用类型参数,可以用任何类型进行替换。
这样构建的列表可以避免对所有索引进行遍历,并允许我们动态地构建列表,而不必预先创建集合并填充它。例如,下面是对列表中所有整形(int)元素进行求和的函数:
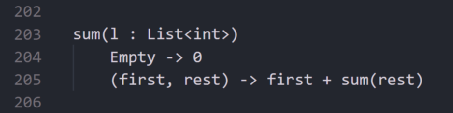
遍历列表
所以我们只需要考虑列表的两种状态:当它为空的时,和是0;当有第一个元素和其余元素时,和是第一个元素加上其余元素的和。
这是多么简单、方便啊!
假如你只想取索引为偶数的元素,最直接的方法是用i进行循环并判断它是不是偶数,但也可以用以下方法:
(1)如果列表为空,那就返回空列表。
(2)如果只有一个元素,那就返回包含这个元素的列表。
(3)如果列表有两个元素及剩余部分元素,那就取第一个元素和剩余部分元素的函数递归结果。
按照上述过程,写出的代码如下:
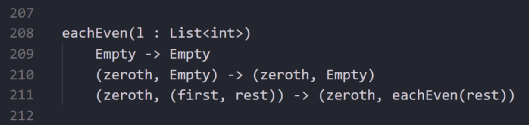
遍历列表
这种类型的列表叫做单链表(singly linked list)
相互递归
相互递归的含义是用B定义A,同时B又是通过A定义的,并且在这个循环中可以有任意数量的“实体(entities)”。红绿树(Red-green trees)就是通过相互递归定义的。通常这种类型的递归比较少见。
语言支持
以上,已经展示了如何在大多数通用编程语言中使用递归方法来代替生硬和可读性差的代码。
同时,还可以通过语言的语法、数据结构和编译工具的特殊功能继续对递归进行优化。
优化尾递归
尾调用优化(TCO,tail call optimization)是指将尾递归编写成实际的循环,常用编译器进行优化,以便让递归定义的函数与循环一样高效。
下面来谈谈调用问题。当调用函数时,会保存当前指令,然后调用函数,调用后又会返回执行前的指令。
如果你想在调用后继续完成某些功能,就必须按照上述过程进行。例如,对于定义为n *factorial (n-1)的阶乘计算,你想在调用内部阶乘函数之后,再将结果乘以n后返回。
那它的伪代码如下:

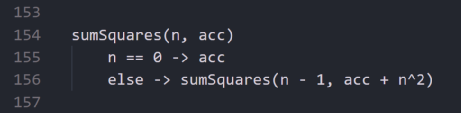
sumSquares的伪代码
sumSquares的功能是将从0到n的整数平方进行相加。因此,当输入参数为0时,将0赋给返回值,并跳转到返回地址。否则,我们保存当前地址,递归调用sumSquares (n-1),与n²相加,然后跳转到返回地址。
如果在函数调用后不进行任何操作,就可以直接跳转。比如从累加器“accumulator” 中添加参数“acc”来实现累加。其具体实现如下:
利用累加器的递归定义
它看起来与我们最初讨论的循环非常接近,用“i”替换“n”,用“sum”替换“acc”,就会变成循环操作。因此,其伪代码如下:
可以直接转换的伪代码
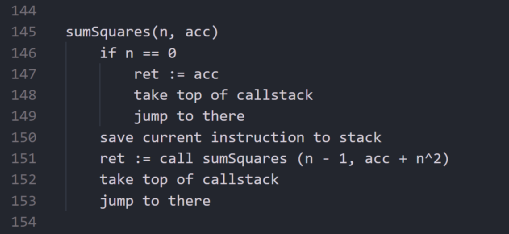
但是事实上,调用时会把结果放入ret中,所以把调用的结果赋值给ret是完全没有必要的。而且如果我们只想要函数返回的值,其实并不需要跳回到原来的地址。如果在调用“ret”后包含所需的值,那么我们只用跳转到自己并结束函数运行即可。

用跳转代替尾调用
将其反编译为伪代码如下:

反编译后的伪代码
事实上,这是一种while循环,可以理解为:如果n是零那么返回,否则运行某些代码后跳转到开头,其功能与下面的while循环等价:

因此,当你用递归方法编写函数后,编译器会自动把它展开成循环!
但可惜的是,并不是所有的编译器都支持该功能,只有在有tailrec的Kotlin、F#(和ML系列)、Scala和其他一些编译器中可以使用。
数据结构
虽然递归不必处理不可变结构,但它可能需要动态地构造新对象。比如F#语言中就包括:
(1)单链表
(2)通过红黑树构成的Persistent maps 和sets
(3)可识别联合(DUs)
我们的目的是让人们在不损害其他方面的情况下使用递归函数,减少潜在的错误或误差。
语法
当有合适的语法支持时,编写递归定义的函数就会更加容易,比如有以下支持时:
(1)用于考虑不同情况的模式匹配(pattern matching)
(2)构造和解构列表和元组
例如,通过decorators,编程语言就可以提供缓存函数(memoize)的方法。
还有一些语言可以确保函数进行TCO优化。例如,Kotlin提供了“tailrec”功能,它会在无法优化时给出警告。
无法使用递归的情况
递归只是一种工具。如果是函数只调用自身不超过一次的单递归的操作,就可以使用顺序进行,比如C#中的LINQ,Kotlin中的sequences等等。
所以只有当递归比它的替代方法更好时,才需使用递归方法。比如写一个过滤偶数的显式函数时,就应该使用filter顺序函数。
或者当编译器不支持TCO,或者函数不受TCO约束,但有成千上万次嵌套调用时,递归方法会消耗大量的堆栈,甚至达到溢出。但日常使用中,很少通过函数遍历这么大的序列。