这个排序这么酷，为什么知道的人很少？-技术圈

有一种很神奇的排序，基数排序(Radix Sort)，时间复杂度为O(n)，今天花1分钟，通过几幅图，争取让大家搞懂细节。

画外音：居然还有时间复杂度为O(n)的排序算法？不但有，其实还有很多。

举个栗子：

假设待排序的数组arr={72, 11, 82, 32, 44, 13, 17, 95, 54, 28, 79, 56}

基数排序的两个关键要点：

（1）基：被排序的元素的“个位”“十位”“百位”，暂且叫“基”，栗子中“基”的个数是2（个位和十位）；

画外音：来自野史，大神可帮忙修正。

（2）桶：“基”的每一位，都有一个取值范围，栗子中“基”的取值范围是0-9共10种，所以需要10个桶（bucket），来存放被排序的元素；

基数排序的算法步骤为：

FOR (每一个基) {

//循环内，以某一个“基”为依据

第一步：遍历数据集arr，将元素放入对应的桶bucket

第二步：遍历桶bucket，将元素放回数据集arr

}

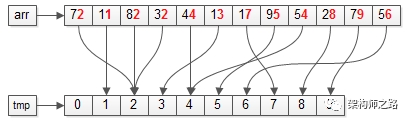
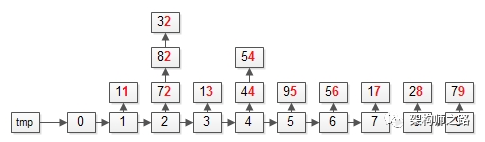
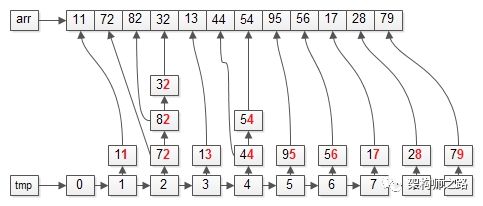
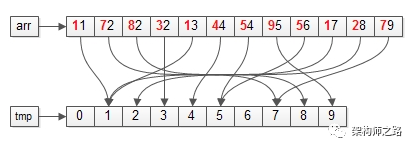
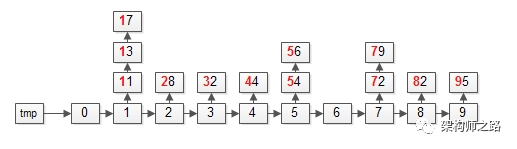
更具体的，对应到上面的栗子，“基”有个位和十位，所以，FOR循环会执行两次。

第一次：以“个位”为依据。

画外音：上图中标红的部分，个位为“基”。

第一步：遍历数据集arr，将元素放入对应的桶bucket；

操作完成之后，各个桶会变成上面这个样子，即：个位数相同的元素，会在同一个桶里。

第二步：遍历桶bucket，将元素放回数据集arr；

画外音：需要注意，先入桶的元素要先出桶。

操作完成之后，数据集会变成上面这个样子，即：整体按照个位数排序了。

画外音：个位数小的在前面，个位数大的在后面。

第二次：以“十位”为依据。

画外音：上图中标红的部分，十位为“基”。

第一步：依然遍历数据集arr，将元素放入对应的桶bucket；

操作完成之后，各个桶会变成上面这个样子，即：十位数相同的元素，会在同一个桶里。

第二步：依然遍历桶bucket，将元素放回数据集arr；

操作完成之后，数据集会变成上面这个样子，即：整体按照十位数也排序了。

画外音：十位数小的在前面，十位数大的在后面。

首次按照个位从小到大，第二次按照十位从小到大，即：排序结束。

神奇不神奇！！！

几个小点：

（1）基的选取，可以先从个位开始，也可以先从十位开始，结果是一样的；

（2）基数排序，是一种稳定的排序；

（3）时间复杂度，可以认为是线性的O(n)；

希望这一分钟，大家有收获。

架构师之路-分享可落地的技术文章

推荐阅读：

调研：

你知道哪些排序算法，时间复杂度是O(n)吗？