困扰数学家50年的问题，竟被博士小姐姐用一周业余时间解决了

▲Lisa Piccirillo

Lisa本人也因此获得了MIT的tenure-track预聘职位，前途无量。

其实这篇论文最早是Lisa在2018年读博期间完成的，当Lisa偶然得到这个结果的时候，她并没有意识到这个问题的重要性。

有一天，她把自己的解决方法告诉了同在德州大学奥斯汀分校的Cameron Gordon教授。Gordon教授大叫道：“什么？我现在就要去投顶级期刊！”

这一举动甚至吓到了Lisa。

直到今年2月，这篇文章才被刊登在学术杂志《数学年刊》上。想必康威在得知自己提出的问题被解决后，也会感到欣慰吧。

01 什么是扭结

「结」这个概念，在日常生活中常被看成是一根有头有尾的绳子打成的结。但数学家眼中的「结」，是一个首尾相连的闭环结，这种结是无法被解开的。

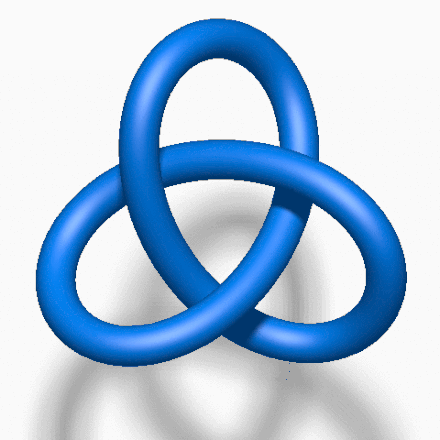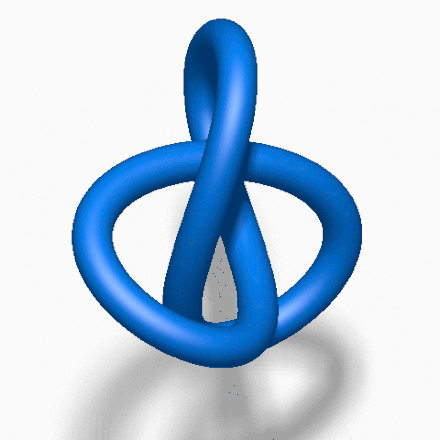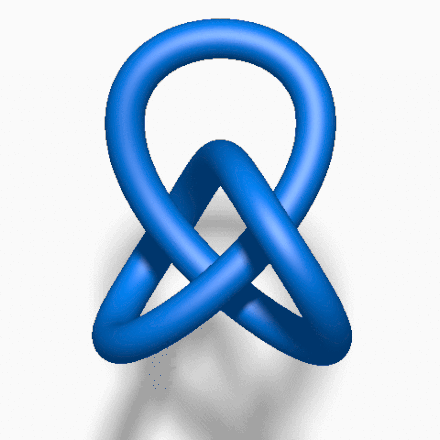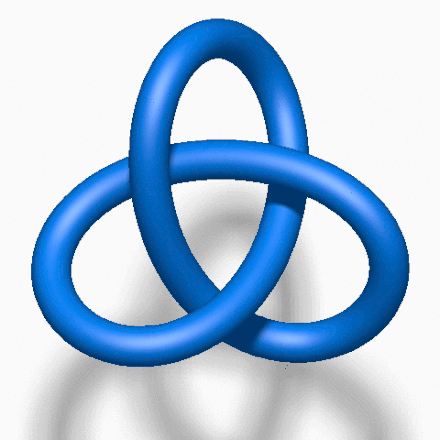
自上个世纪以来，有关扭结的研究启发了量子力学、DNA结构和三维空间拓扑学。

所以数学家们自然要发问，在4维空间中是否有与三维空间对应的扭结理论。

但是这里存在一个问题：在第四个维度上，扭结的绳体可以互相重合穿越，这样一来，任何扭结都可以解开了。

所以4维空间的扭结不是三维扭结的简单移植。

4维空间的扭结并不好理解，我们可以借助3维空间中的的一个球体来想象。

如果切开一个3维球体，可以得到一个未打结的圆环。切开一个4维空间的扭结球体，你可能看到一个打结的环，或者是一个未打结的闭环。

任何能用这种「切开」一个扭结球体而得到的扭结，都称它们为「可切的」（slice），即片状结。但也有一些「不可切」的扭结，比如有3个交叉的三叶结。

片状结提供了3维和4维扭结理论的桥梁。

在4维拓扑学中，片状结有两种形式，一种1980年代年提出的理论认为，在4维空间中，不只有我们常规认知的平坦光滑球体，还普遍存在一种皱缩球体，且永远无法被拉平。所以4维空间中的扭结是否可切，取决于这些特殊的皱缩球体。

这种皱缩的球体并不是4维空间的异常，而是一个十分有用的特征。4维空间中的片状结是「拓扑可切」，而不是「平滑可切」。

这意味着数学家可以借此构造不同版本的普通四维空间，这种4维空间在拓扑学上与其他没有不同，只不过是褶皱的。

切片性问题是这些奇异的四维空间的 “最低维度探究”。

02 康威扭结

多年来，数学家们发现了形形色色的扭结，这些结在拓扑学上可切，但并不是平滑可切。然而，这些扭结的交叉都大于12。而在交叉点数小于12的扭结中，只有康威结的切片状态却一直无法找到。

▲剑桥大学牛顿数学科学研究所的大门，用康威扭结来做装饰

康威在上世纪50年代时对扭结理论产生了浓厚的兴趣。

他想出了一个简单的方法，把交叉点数目不同的的扭结一一列出来，而前人将这项工作推进到10个交叉的扭结。

康威列出了所有具有11个交叉点的扭结，很快发现了它们的特殊之处，这些就是康威扭结。

▲图中只画到了7个交叉的扭结，交叉点是两条绳体交叉之处

11个交叉点的康威扭结，是拓扑可切的，但数学界一直无法证明它是否平滑可切。

数学家马克·休斯（Mark Hughes）创建了一个神经网络，利用扭结的不变量和其他信息来预测可切性等特征。对于大多数的结，这种神经网络能够做出明确的预测。但它对康威结是否具有平滑可切性却没有确切答案。

康威扭结是否平滑可切之所以如此重要，不仅因为它困扰了数学界半个世纪。

平滑可切的扭结为数学家提供了一条探索四维空间奇特属性的途径。

而证明康威扭结是否为平滑可切，已经成为扭结理论重大突破的硬标准。

03 问题解决

数学家一直怀疑康威结不是平滑可切的，因为它缺乏一种 “带状性 “的特征，而平滑可切的扭结通常具有这种特征。

但康威结也有一个特点，使它对所有试图证明它不是光滑切片的尝试都无功而返。

康威扭结有一种变体，如果我们把康威扭结画在纸上，把它的下半部分剪下来，翻转180度再接上，那么就得到一个Kinoshita-Terasaka扭结。

巧合的是，后面的扭结是平滑可切的。

Lisa本人喜欢扭结理论所需的视觉直觉，但她并不是扭结理论方面的专家。Lisa在波士顿大学读本科期间的老师Elisenda Grigsby，Lisa当时并没有展现出天才少年的潜质，但是她的创造力吸引了Grigsby教授的注意。

Grigsby教授说：“她非常相信自己的观点，并且一直如此。”

Lisa当时正在思考关于康威扭结的问题，当时她正在考虑除了突变外将两个结关联起来的另一种方式。每个扭结都有一个关联的四维形状，它是通过将结放置在4D球的边界上并沿着结在球上缝制某种帽而制成，数学家称之为迹（trace）。

Gordon表示，迹以一种非常强烈的方式编码了扭结。

不同的结可以具有相同的四维迹，数学家发现相同迹的扭结总是具有相同的可切性质：要么都是可切的，要么都不是。但是Lisa和莱斯大学博士后Allison Miller证明，可以将扭结迹的不变性让我们在研究扭结可切性质的时候，构造相似扭结变得非必要。

这为Lisa证明康威扭结非平滑可切提供了一种策略：如果可以为康威扭结构造一个相同迹的扭结，那么也许可以更好地与可切不变性配合使用。

构造这样同迹的扭结并非易事，但是Lisa却有非常的天赋，她只是回到家中研究就做到了这一点。

通过巧妙的扭结的组合，Lisa设法构造了一个复杂的扭结，它的迹与康威扭结相同。Lisa使用了一种叫做拉斯穆森S不变量（Rasmussen’s s-invariant）的工具，结果显示她构造的扭结不是平滑可切的，因此康威扭结也不是。

“这是一个非常美丽的证明，”戈登说。没有理由指望Piccirillo构造结会产生拉斯穆森的小号 -invariant，他说。“但是它起作用了……有点令人惊讶。”

Gordon给了Lisa很高的赞誉：“这是一个非常美丽的证明。”他完全没想到Lisa用这样一种用具实现了证明。

Lisa的本科论文导师Greene说：Lisa的工作说明拓扑学家对扭结迹的认识还存在着不足。

参考资料：
https://www.quantamagazine.org/graduate-student-solves-decades-old-conway-knot-problem-20200519/
https://mathworld.wolfram.com/SliceKnot.html
https://www.maths.ed.ac.uk/~v1ranick/papers/sliceknots2.pdf

论文地址：
https://arxiv.org/abs/1808.02923