群体智能算法——烟花算法
烟花算法是我在观察现实中的烟花在空中爆炸这一现象,受到启发而提出的一种具有爆炸搜索机制的全局优化求解的新型群体智能算法,它在求解复杂优化问题中表现出了非常优良的性能和很高的效率,已经逐渐获得了业界的高度关注和跟踪研究。通过近5年的发展,已经相继提出了二十余种烟花算法的改进方法、收敛性分析和多项典型应用,逐渐发展成为一种十分有效的群体智能算法。
记得小的时候在四川老家,每逢一年中最重要的节日春节到来时,我都会邀上几位要好的小伙伴或同学一起到空旷的操场或人烟稀少的街道上,尽情燃放一种在空中爆炸的爆竹花炮。有时,几个小伙伴还会一起进行比赛,看看谁的爆竹扔得高、放得响,在空中燃放出最美丽的图像。这些都是伴随着我们儿时快乐和美好的时光,在我儿时的脑海里留下了很深的印迹。
2006 年春节,我来北京大学任教将近一年了。在这段时间里,我对进化计算投入了较多的精力,进行了深入的研究。因此,在这段时间不管在干什么和遇到什么新鲜的事物都会看看它们是否与进化计算能联系上。恰好在这一年春节期间,北京将禁放烟花爆竹的规定改为限放,首都市民都迫切地期待着除夕之夜的到来,盼望着过一个更加热闹和欢庆的春节。这年的除夕之夜,北京的天空尽情地开放,市民们都争相燃放。人们燃放出了大量绚丽多彩的礼花,将漆黑的夜空照得亮如白昼,五彩斑斓的烟花,燃放出各种美丽的图像,激发了我内心深处的儿时回忆,心情无比的畅快和愉悦。
此时,我的脑海里突然将烟花的爆炸图像与进化计算中随机搜索建立起了联系,产生了一种可以用像烟花爆炸图像一样的方式来对问题解空间进行有效搜索的新方式。
通过模拟烟花爆炸的方式来进行多点同时爆炸式搜索,这也许是一种高效的搜索方式,是有别于现有其他方法的新型搜索方法,从而有了研究这种爆炸搜索方式的想法,当时为其取名烟花算法(fireworks algorithm,FWA)。
虽然烟花算法这个名称比较直观和简洁,但是由于它没有直接与优化等求解问题建立直接的联系,此后有些研究人员有时也用其他别称来称呼我们的烟花算法,如烟花优化算法、烟花爆炸算法、烟花爆炸优化算法、烟花爆炸搜索算法、爆炸搜索方法等。尽管有这些不同的别称,这里统一采用原始的名称烟花算法,以免混淆。
我们对烟花算法的研究动机是希望寻求一种求解复杂问题的全局最优解的高效方法。尤其是对具有多模特性的复杂优化问题能够找到高效求解的新途径。
在2006 年的夏季学期,我招收了来自吉林大学的朱元春同学做我的直博生,并安排他来我的实验室从事毕业设计工作。我将之前的想法和研究烟花算法的任务交代给他来实现,并将他的毕业设计题目拟定为“烟花算法的研究与实现”,与他一道开始了对烟花算法的全面研究。
经过半年时间的深入研究,我们共同设计了烟花算法的各个主要要素、组成和基本框架,并以“爆炸算子”为基础搭建了基本的烟花算法。到2007 年5 月份,我们就完成了对烟花算法的基本研究工作。
但是,在接下来的近两年的时间里,因为忙于主持一项国家863 计划项目,只得暂缓了对烟花算法的相关研究工作,直到2009 年夏才有机会重新展开对烟花算法的研究。2010 年,在首届国际群体智能大会上发表了题为“Fireworks algorithm for optimization”的开创性学术论文。自此烟花算法的研究开始受到业界的关注,对其的研究才开始在群体智能领域逐渐展开。
群体智能(swarm intelligence,SI) 是指由许多简单个体组成的群体呈现出的涌现(emergence) 行为所表现出的集体智能,是单个个体所不具备的强大能力,如生物群体系统有蚁群、鸟群、蜂群、鱼群、蜘蛛、萤火虫、细菌等。鸟群掠过天空、蚁群寻觅食物、鱼群在水中游荡、烟花在空中爆炸、蜘蛛的爬行等,这种群体的运动称为群体行为。尽管这些群体中的每个个体都非常简单,但大量个体组成的群体所表现出的集体行为却是非常复杂的,呈现出了智能的特色。
群体智能是进化计算的一个活跃分支,隶属于计算智能的范畴。近几十年来,计算智能领域取得了丰富的研究成果,包括人工神经网络、模糊逻辑与系统、进化计算、混沌计算、模拟退火、禁忌搜索,以及各种混合策略等,都是通过模拟或揭示某些自然现象或过程来实现的。
优化问题是一个古老且永恒的研究问题,也是解决众多问题的基础。大量学者和实际工作者都致力于对其进行不懈的研究。不同于经典优化算法采用确定性规则的方式,群体智能优化算法利用一种概率转移方式,通过各种随机因素结合元启发性规则,采用群体中的多个个体同时对解空间进行并行搜索的方式,通过群体中个体的相互协作与竞争来实现对优化问题的最优解的有效搜索,具有随机性、自适应性、鲁棒性、并行性等显著特点。在求解复杂优化问题时,群体智能优化算法表现出了非常明显的优势,引起了人们的高度重视,成为目前的研究热点。
群体智能优化算法可以分为基于生物群体的群体智能优化方法和基于非生物群体的群体智能优化方法。
前者包括蚁群优化、粒子群优化、鱼群搜索、虚拟蜜蜂算法、萤火虫算法-I、萤火虫算法-II、布谷鸟算法、蝙蝠算法、人工蜂群算法、人工鱼群算法、磷虾群算法、细菌觅食优化算法等。后者包括烟花算法、水滴算法、头脑风暴优化算法(BSO)、磁铁优化算法等。目前,群体智能算法研究主要包括理论、算法、求解问题类型、应用。其发展趋势包括混合算法、求解大规模问题(面临维数灾难、大数据难题)、新型改进算法、理论分析等。
通常,群体智能优化算法都有一定的共性,即由组成群体的多个个体(社会昆虫、或粒子) 的相互协同,具有交互传递信息(直接或间接地) 和交互式地适应环境的能力,使群体中的个体对环境的适应性逐代变得越来越好,逐渐求得问题的全局最优解的足够好的近似解。
群体智能优化算法所具有的这种协同交互能力能够打破没有免费午餐(NFL)定理的魔咒,预示了存在并且能够发展出具有性能更加优良的高效算法。
这预示着对群体智能优化算法的深入研究将可能给我们带来难以预想的益处,因此激励更多的研究人员从事群体智能的研究和在更多的实际领域里积极采用群体智能的最新研究成果,使得群体智能可以更好地为人类社会服务。
3、烟花算法的组成与研究内容
烟花算法的基本组成框架如下图所示,主要由爆炸算子(explosive operator)、变异操作(mutation operation)、映射规则(mapping rule) 和选择策略(selection strategy) 四大部分组成。爆炸算子包括爆炸强度、爆炸幅度、位移变异等操作;变异操作主要包括高斯变异操作等;映射规则包括有模运算规则,镜面反射规则和随机映射规则等操作;选择策略包括有基于距离的选择和随机选择等操作。
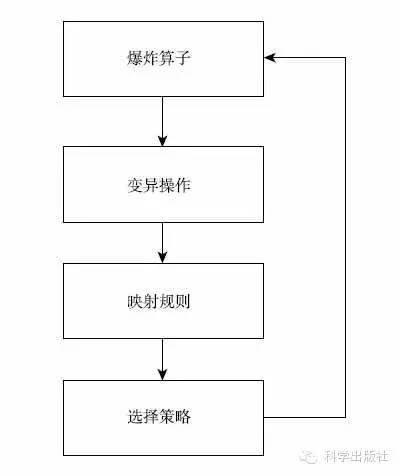
图 烟花算法的基本组成框架图
烟花算法的工作过程与一般群体智能优化算法相似,首先随机选择N个烟花初始化群体,然后让群体中的每个烟花经历爆炸操作和变异操作,并应用映射规则保证变异后的个体仍处于可行域内,最后在保留最优个体(即精英策略) 的前提下,应用选择策略从生成的所有个体(烟花和火花) 中选择出余下的N-1 个个体共同组成下一代的群体。这样周而复始,逐一迭代下去。通过这种交互传递信息(直接或间接地) 使群体对环境的适应性逐代变得越来越好,从而求得问题的全局最优解的足够好的近似解。
目前,对烟花算法的研究工作主要包括理论分析、算法研究、求解问题类型和应用研究。
(1) 理论分析。研究烟花算法的求解机理、收敛性质、演化轨迹特点,各参数对算法性能的影响等理论问题,为开发新的算法和改进现有算法提供理论指导。
(2) 算法研究方面。在算法研究方面,通过对烟花算法基本组成的各个成分进行深入分析和调整,不断改进烟花算法的性能(收敛性、解的精度、时间效率),提出了各种不同的改进烟花算法。同时,通过与其他方法的结合,取长补短,发展出高效的混合型方法。
(3) 求解问题类型。由于烟花算法的通用性,可以用于求解下列不同类型的问题,即单目标优化问题、约束单目标优化问题、多目标优化问题、约束多目标优化问题、许多目标优化问题、组合优化问题(combinatorial optimization problem,COP)、动态优化问题(dynamic optimization problem,DOP)、其他优化问题。
(4) 应用。烟花算法是一类群体智能优化方法,具有求解复杂问题的全局最优解的能力,同时对求解问题的目标要求很低,不要求问题的目标函数的梯度信息,所以具有广泛的适应性。因此,烟花算法可以应用到许多实际应用领域,求解人们可能遇到的各类问题。
烟花算法不仅继承了现有群体智能优化算法的许多优点,还具有明显的自身特色,归纳起来,烟花算法具有下面一些优点。
(1)爆发性(explosive)。每次迭代开始,需要让烟花进行爆炸,在辐射范围内产生许多与该烟花本身不同的火花。之后,依据特定选择策略选择N 个火花或烟花做为下一代烟花群体,恢复烟花数目,并为下次爆炸过程做好准备。
(2)瞬时性(instantaneity)。烟花算法中爆炸产生的火花,如果没有在选择策略中被选中成为下一代的烟花,这些火花或烟花本身都将在本次迭代中消亡,也就是说,一次特定的爆炸只存在于一次特定的迭代之中,具有瞬时存在性。
(3)简单性(simplicity)。每个个体只能感知局部信息,个体的能力或遵循的规则非常简单,因此算法的组成和实现都非常简单。
(4)局部覆盖性(locality)。对于某一个烟花而言,它的爆炸范围是整个自变量取值范围的一个小部分,其爆炸出的火花是这个爆炸范围内的一些局部点,只是对爆炸范围的区域内的点有一定程度的随机覆盖,但是不会涉及爆炸范围外的点,因此说这种爆炸具有一定的局部性。
(5)涌现性(emergent properties)。使用简单交互规则,通过协同与竞争方式个体间相互作用,其群体总体表现出来的单个个体不具有的复杂行为,呈现出智能的特点。涌现现象是以相互作用为中心的, 它比单个行为的简单累加要复杂得多。
(6)分布并行性(distributed parallelism)。群体中个体相对简单,没有一个直接的中心控制约束,每个个体进行局部相互作用,本质上是一个分布式方法,呈现出高度并行的特色,特别适合并行化处理。
(7)多样性(diversity)。首先,烟花个体的多样性,我们通过一定的选择机制,使选择保留下来的烟花具有不同的位置,以保证算法的多样性特征。其次,爆炸强度和爆炸幅度的多样性,即在爆炸强度的作用下,根据各个烟花的优良度不同(适应度函数值大小不同),各个烟花产生不同个数的火花。在爆炸幅度的作用下,根据各个烟花不同的优良度,各个烟花产生的火花拥有不同的变异幅度。最后,爆炸算子中的多种变异共存,正如烟花有多个隔层那样,我们设计出的爆炸幅度中存在有多种变异。目前有两种变异:一种是位移变异;另一种是高斯变异。其中,第一种位移变异是跟自变量的取值区间,以及粒子本身的优良度(决定了变异幅度的大小) 相关的一种变异;第二种高斯变异只与烟花本身的位置有关。这两种变异是本质上不同的变异,保证了变异的多样性。
(8)可扩充性(scalability)。由于个体相对独立,个体间的协作通常通过间接的方式实现信息交流,增加或减少部分个体,对系统的影响都不剧烈,从而保证系统具有很强的可扩展性。
(9)适应性(adaptability)。由于只使用各个个体的适应性来对系统求解能力进行评估,因此对所求解问题的要求非常低,甚至不要求所求解问题具有显式的表达。

本文由刘四旦摘编自谭营著《烟花算法引论》一书。《烟花算法引论》系统描述了作者提出的一种新型群体智能算法——烟花算法,它的产生、算法实现、理论分析、算法改进及其应用,为读者勾勒出了烟花算法的全景图像。主要内容包括:烟花算法的基本原理与实现及其性能分析、收敛性和时间复杂度分析、多种改进算法、混合方法、离散烟花算法、烟花算法的并行化实现,以及几种应用实例。书中重点介绍了烟花算法的参数设定,各种改进方法、并行化实现、与典型群体智能算法的性能对比分析等、书中还包括了烟花算法的最新资料和一些重要算法的流程图,以及源代码的链接,供感兴趣读者参阅和使用。