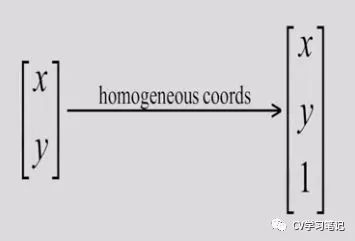
原来你是这样的齐次坐标
点击左上方蓝字关注我们

转载自 | CV学习笔记
今天我们来学习齐次坐标和齐次坐标系,如果你是工科生或是理科生一定听说过齐次这个词,线性代数中我们曾经提到过齐次线性方程组,百度百科的将齐次线性方程组解释为“常数项全部为零的线性方程组”。这个解释非但没有告诉我们 [齐次] 是什么,反而让我们更糊涂了!
我们先从从字面上看一下 [齐次] 是什么意思,齐次的英文是 homogeneous 译为相同的,同质的,同类的。以刚刚提到的齐次线性方程组为例,我们知道 Ax = 0 就是齐次的, Ax = b 不是齐次。当我们把方程左边 Ax 放大一个常数倍时,齐次的 Ax = 0 依然成立,而非齐次的 Ax = b 则不再成立。换句话说对于 mAx = 0,m 为任意非零实数,他们本质上都是同一个方程组,也就是所谓的同质性。再简单来讲,齐次性就是输入函数扩大 a 倍,而其响应函数相应的也扩大 a 倍,就叫 [齐次性]。
那么齐次坐标呢,我们可以理解为(x, y, z)和(kx, ky, kz) 表示同一点,其中k ≠ 0。有的同学可能问了,(x, y, z)和(kx, ky, kz)明明是两个不同的点啊。你说的没错,对于三维空间的点,这的确表示两个点,但是我要用它表示的是平面中的点。你又会说了,这不是浪费吗,明明只有两个自由度为什么非要用三个参数表示。不知道大家看过三体没有,低维文明对高维文明的攻击是毫无抵抗力的。那么我们用三维的方法去解决二维的问题想必也会是轻松加愉快。
现在就来一起看看这一切是如何做到的。
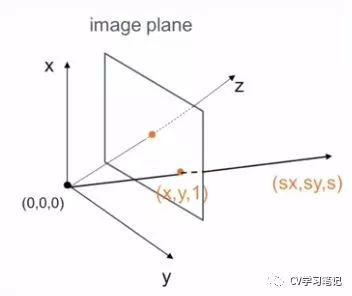
当我们看一个二维图像,每个点都有一个坐标,可以用 x,y 表示。但是如果把它想成一个三维空间上的点。当我们看到这下面张图片时,想象我们和成像平面间有一定距离。可以假设我们的观察点在三维世界中坐标为 (0, 0, 0) ,成像平面在我们的前方一个单位的位置上,成像平面上的一个点将不再是一个点,而是一条经过我们眼睛和成像平面该点的一条射线,也就是一条过 (0, 0, 0) 和 (x, y, 1) 的射线。这样图片中的一点就和三维世界中的一条线联系起来。从现在起,我们每看到一个点都是一条射线,我们用齐次坐标第三个维度坐标的倒数表示我们研究的点在 z 方向(垂直于成像平面)距离我们多远。
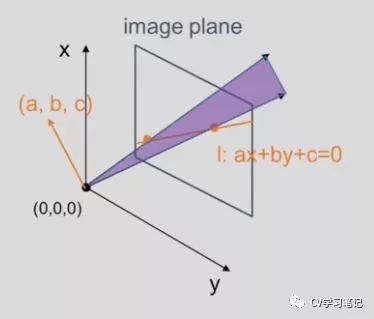
既然图片中一点表示一条三维射线,那么图片中一条线对应在三维空间是什么呢?
相信聪明的你已经想到了,没错就是一个由直线端点表示的那条射线沿直线掠过到另一端点的面,如果平面中是一条直线,就对应空间的一个平面,否则就是一个曲面。我们这里只研究平面,用方程 ax+by+cz = 0 来表示。向量形式表示就是
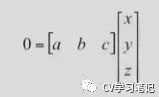
所以一条直线的齐次坐标表示同样是一个三维向量。回忆一下高等数学的知识,其实这个向量的三个坐标表示的就是平面的法线方向。
已知两点坐标求直线方程
我们知道对于平面中的两个点,可以采用两点法解出过这两点的直线表达式,但是计算十分繁琐。对于齐次坐标表示的点和直线呢,我们可以用一种高维的方法去解决这个问题。既然平面上的直线对应空间的一个平面,而这个平面又是由它的法向量表示的,显然这个法向量垂直于平面上任意的直线,当然也垂直于平面上两个点对应的射线。

想到这里,我们就可以利用两个射线的叉乘得到与他们垂直的向量,也就是所求平面的法向量,即所求直线。
所以平面中直线表示为
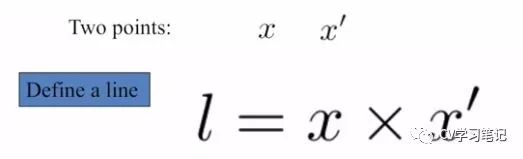
已知两直线求交点
如何找到两条直线的交点,在平面内我们联立两个直线方程,求解一个二元一次方程组。在齐次坐标系系统中两条直线分别表示了两个过空间原点的平面,成像平面中两直线交点对应空间中两平面相交直线。由高中立体几何的知识,因为该交线同时位于两平面内,所以同时垂直与两平面的法线。
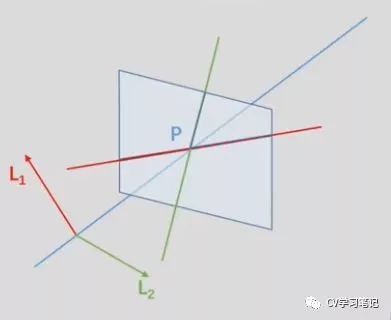
利用两法线叉乘就能得到该交线的方程。
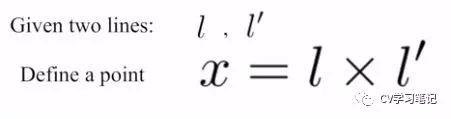
点和线的对偶性
这引出了在齐次坐标下点和线的对偶性。点由三维坐标表示,平面也是。根据这个概念我们可以看到直线 P1P2 ,由过 P1, P2 两点表示的两条射线的叉积定义。因为平面中线代表三维中的一个平面,直线 P1P2 对应的平面有一个法线 n ,同时垂直于空间中的射线 P1, P2 。
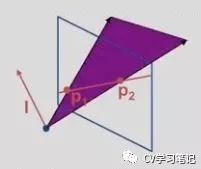
类似的,下图平面中两条红线也是由三维向量表示,平面的法线 l1, l2 由线和原点决定,两条线相交于一个点,同样可以通过计算两个向量的叉积得到交点 又因为交点代表的射线,同时垂直于平面法线l1和l2,因此平面法线 l1 和 l2 的叉积,就是交点射线的方向,也就是交点的齐次坐标。
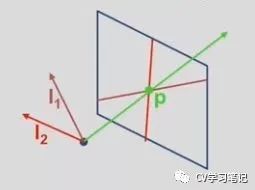
这便是对偶性,因为可以以相同的方式看待点和面首先它们都用三维向量表示,其次你可以通过叉积得到两点连线,而两条线的交点也可以用相同的方法得到。
当我们叉乘得到的结果是 (x, y, 0) 代表什么意思,回忆一下,当我们要把三维射线转换为二维点时需要除掉第三项。但 x 除以 0 , y 除以 0 ,我们会得到两个无限大的数 这意味着这是一个无穷远处的点。事实上有无数个无限远的点,与图像中每个方向的平行线一一相对。
实际上这就是上期提到的灭点!所以,图像中的灭点就是平行线相交得到的。平行线在现实中不相交,但我们仍然可以做一个叉积。考虑平面中两根平行的直线,x = 1,x = 2,齐次坐标为 (-1, 0, 1) 和 (-1 , 0, 2) ,两向量叉积为 (0, 1, 0) ,得到的是交点齐次坐标最后一项为 0 ,故为无穷远处的点,齐次坐标的前两项表示在哪个方向的无穷远处,如 (0, 1) 表示 y 轴方向。
那么无穷远处的直线是什么呢,假设存在一个直线 (a, b, c) 经过所有灭点 (x, y, 0) ,将任意两个无穷远点进行叉积,我们发现这条直线必有 (0, 0, 1) 的形式,这是成像平面的法线,且这条法线垂直于正中心处。
我们称 (x, y, 0) 和 (0, 0, 1) 为理想点和理想线,每一个无限远处的点都表示为 (x, y, 0) 它是一组在成像平面中指向 (x, y) 方向的相互平行的线的交点,所有这些指向同一方向的线有同一个灭点 (x, y, 0) ,而这个理想点坐标表示的直线,是在成像平面中是一条穿过原点的实际存在的线 ,而理想线坐标表示的点,正是成像平面中的原点。
以上内容来源于对宾夕法尼亚大学在Coursera平台开设的《Robotics》专项课程《Perception》篇的理解和摘要。
END
整理不易,点赞三连↓
