稳赚不赔的方法,有人找到了?

导读:煮熟的鸭子飞得快。

如果他答应,15万美元马上到手,但可能失去赚50万的机会; 如果他不答应,就有机会拿走50万美元,但也可能一分钱都赚不到。
下注者当时可以再下注押B球队赢。这样,不管哪一方获胜,他都可以有可观的收入。
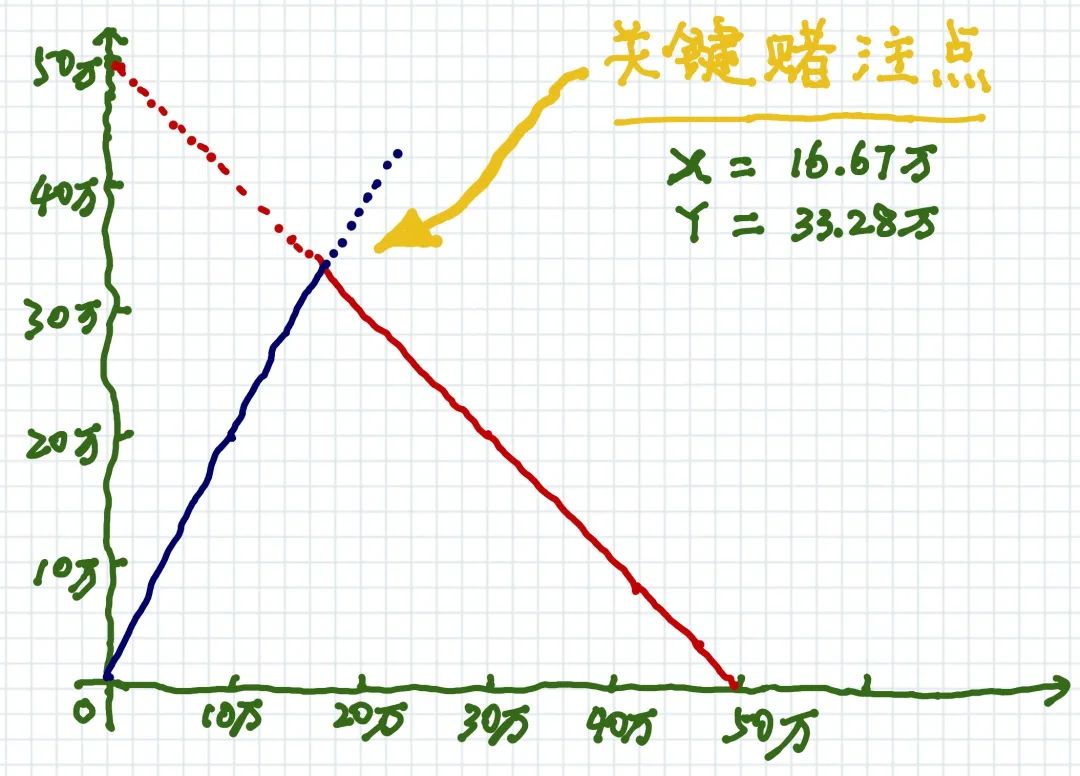
红线是假如A获胜的回报,表示为:(50万-500-B) 蓝线是假如B获胜的回报,表示为:(B✖️3-500-B)

根据期望值理论,绿色按钮价值5千万; 很多人仍然愿意选拿到确认的100万,因为他们无法忍受50%概率的什么都拿不到,因为毕竟这不是一个多次博弈游戏,人生能有几回搏? 换而言之,假如一个人无法承受“什么都没有”,那么右边的选择就相当于“你有50%概率得到一个亿,有50%概率死掉”。你当然无法承受死,何况高达50%概率; 开放地想,假如你拥有这个选择的权利,也就是“概率权”,你可将右侧价值五千万的概率权卖给一个有承受力的人,例如两千万(甚至更高)卖给他; 继续优化上一条,考虑到增加“找到愿意购买你该选择权利的人”的可能性,你可以只用100万(低首付)卖掉这个权利,但要求购买者中得一个亿时和你分成; 再进一步,你可以把这个选择权做成彩票公开发行,将选择权切碎了零售,两块钱一张,印两亿张。头奖一个亿。对比5,风险更低,收益更大; 鉴于6的成功商业模式,开始募集下一笔一个亿作为头奖,令其成为一项生意; 按照P/E估值,募集20亿,公开上市,市值100亿。

算术平均值看,年均回报是25%; 几何平均值看,年均回报是0%。
例如用3%的资产购买“崩盘时能获得900%的超高回报”的保险,这种保险的算术平均回报率是0%,复合平均回报率为-100%,但是却能很好地保护另外97%资产,有效避免整体资产的大幅回撤。
100瓶水空一瓶倒无所谓,因为发挥作用的是99%; 但如果是描述99瓶正常,其中一瓶有毒,那么发挥作用的就是1%。

个人在纸上画了辆车就觉得自己可以造车了; 做了辆玩具车的人,没有意识到,“智慧的投资者对于对上一两次没有兴趣”; 能够接触前沿理论的聪明人,的确可以在实验室里用“Beta、夏普比率、协方差矩阵、肥尾......”造出一辆看上去很厉害的车,甚至可以在某个赛车场上赢几圈儿,然而一进泥地就完蛋。
鲁棒性在进化论里指在突变时生物体的表型仍保持不变的能力。 鲁棒决策,是指一种“尽可能对不确定性免疫”,并在作出后相当长时间仍看上去不错的决策。 鲁棒统计,即使其假设与产生数据的真实模型不符,依然能良好运作的一种统计技巧。

“押注球队”的故事里,是主动降低“整体期望值”; “保险策略”的案例里,是主动降低局部的算术平均值。

在下棋过程中,如果我看到有机会去赢,哪怕是一个子的优势,我就会把优势稳稳守护到最后,而放弃另外一条赢20目以上‘好棋’的路。 一次师傅在复盘的时候跟我说道,你只要走这一步,就能赢很多子了,为什么不下呢? 我说,大胜的棋,也意味着冒大的风险。如果按照我的下法,能够保证赢一百盘棋,而且都是半目胜。
局部最优,有点儿像追求年回报的算术平均值最大; 全局最优,有点像追求复合年化回报率最大(对应几何平均值)。

“为什么你做什么都那么慢呢?” “因为……我害怕。”
我绝不能恐惧。恐惧是思维的杀手。恐惧是带来彻底毁灭的小小死神。我要直面我的恐惧,让它穿越我的身体,当一切逝去,我将打开心眼看清它的轨迹。恐惧所剩无几,唯我独存。
有钱人,是以为稳定的东西一下子垮掉了; 穷人是每次都All in,不断被清空。


延伸阅读👇

延伸阅读《哈佛概率论公开课》
评论
