微软面试题:红帽子与黑帽子
所有人先看别人头上戴的是什么帽子,然后关灯,如果有人认为自己戴的黑帽子,就打自己一个耳光。


一直到第三次关灯,才有声音响起。


分析



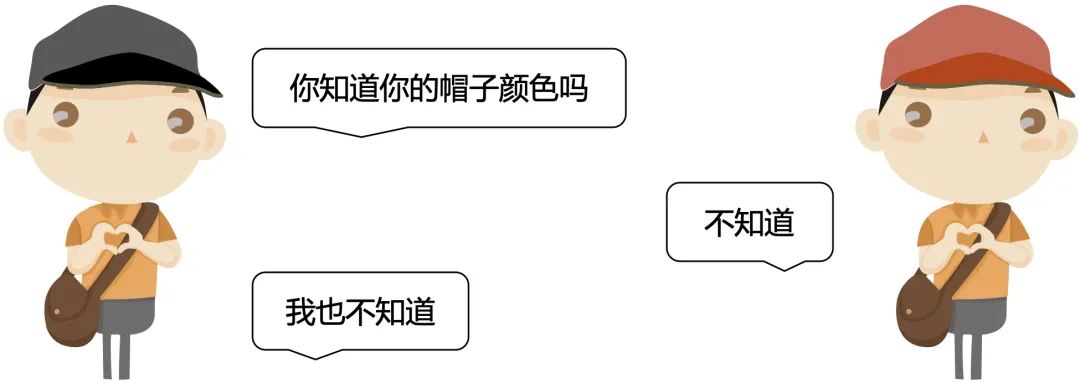
寻找突破口
没有说红帽子有多少人,说明解题的思路肯定跟红帽子没什么关系,有多少都无所谓,那就从黑帽子开始思考。
小规模简单场景

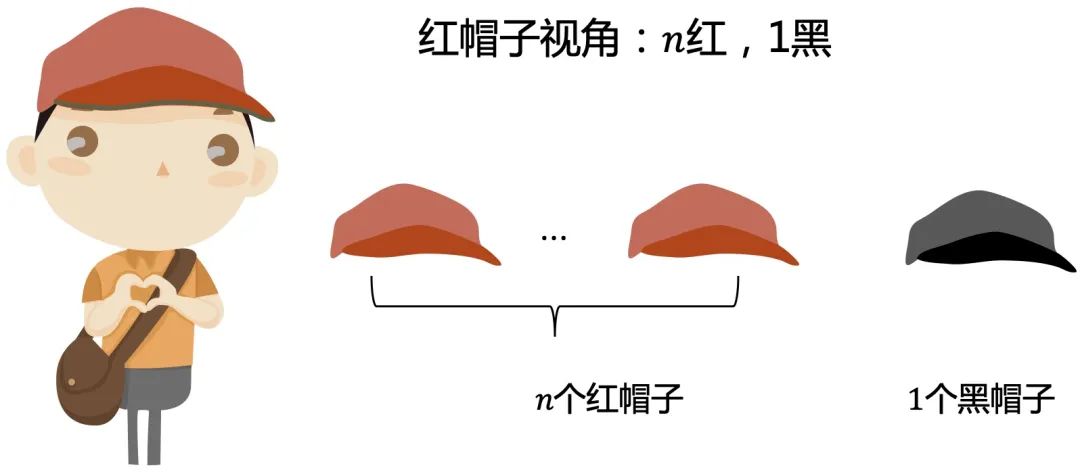
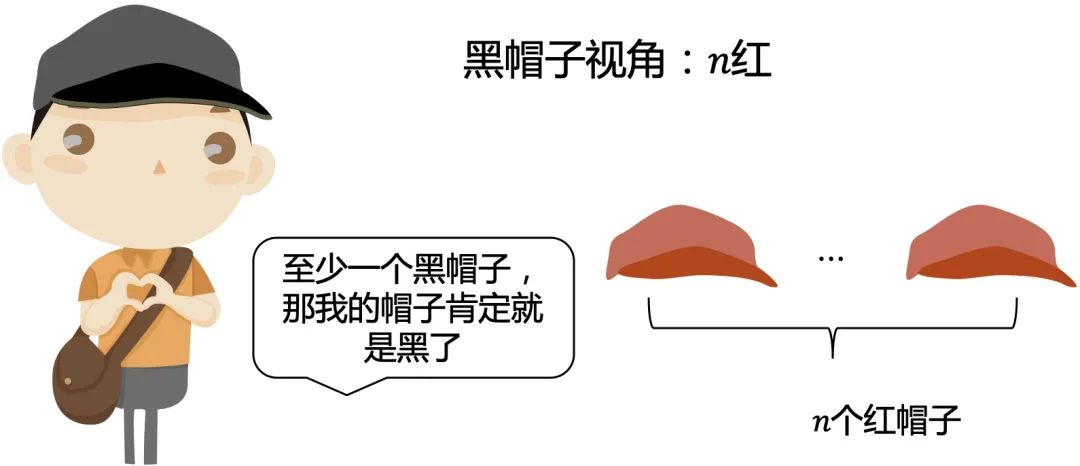

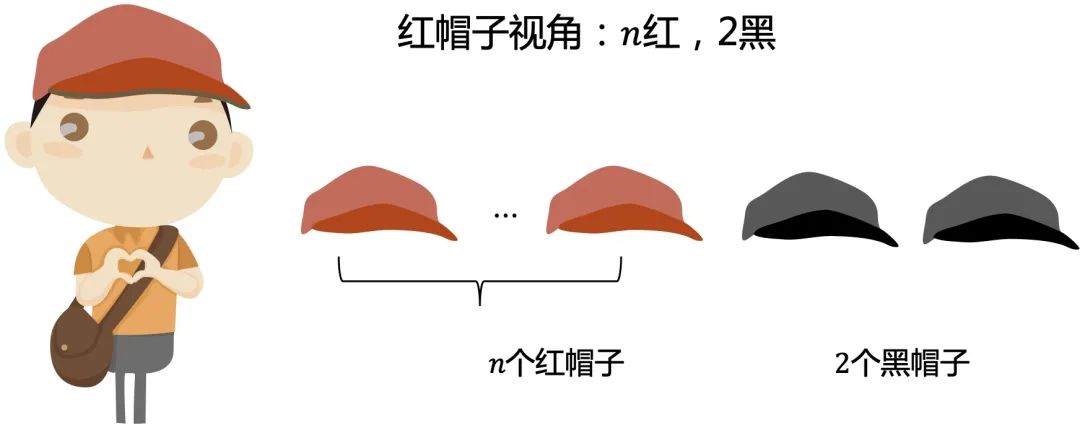
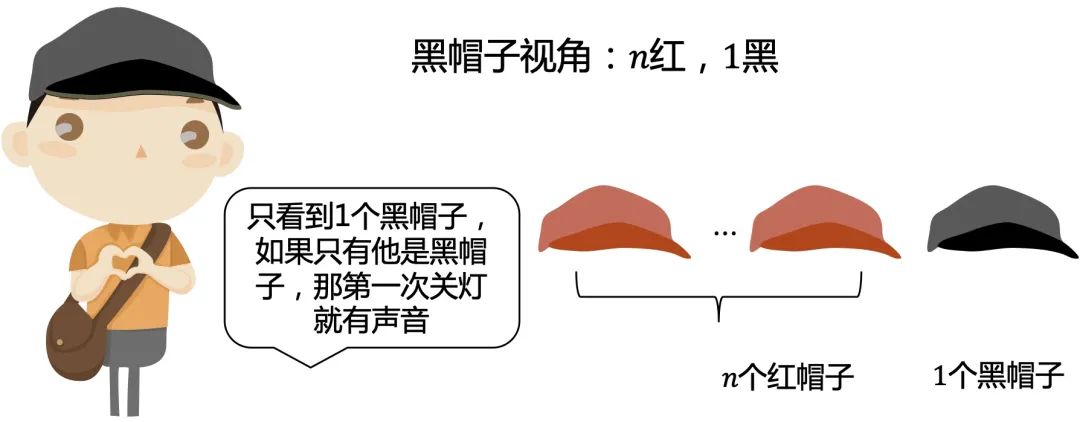
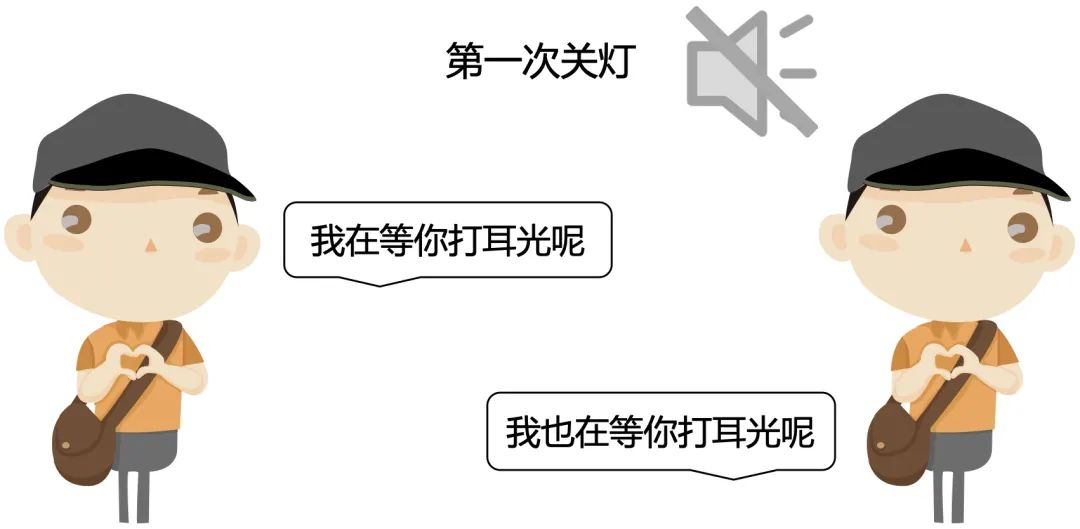





总结
✄------------------------------------------------
双一流高校研究生团队创建 ↓
专注于计算机视觉原创并分享相关知识 ☞

评论
 下载APP
下载APP



分析




寻找突破口
小规模简单场景












总结
✄------------------------------------------------
双一流高校研究生团队创建 ↓
专注于计算机视觉原创并分享相关知识 ☞
