力扣:地下城游戏,手把手教你做困难题

174. 地下城游戏 【困难题】【动态规划】
一些恶魔抓住了公主(P)并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士(K)最初被安置在左上角的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快到达公主,骑士决定每次只向右或向下移动一步。
编写一个函数来计算确保骑士能够拯救到公主所需的最低初始健康点数。
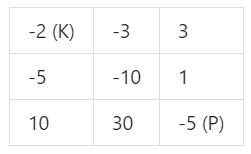
例如,考虑到如下布局的地下城,如果骑士遵循最佳路径右 -> 右 -> 下 -> 下,则骑士的初始健康点数至少为 7。
题目讲解
【核心思想】
这道题,第一眼看过去就是一道动态规划题。但为什么这是困难题呢?因为这与普通的动态规划不一样,注意这一句如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。也就是说,它不是简单的求最小值的问题,其中还有一定的约束。
举个例子:
| 1(K) | -3 | 3 |
|---|---|---|
| 0 | -2 | 0 |
| -3 | -3 | -3(P) |
这个例子中如果只看走到格子(1, 2)的结果的话,肯定是 下 -> 右 -> 右 最好,因为这样初始生命只需要 2 就够了。而另一条路 右 -> 右 -> 下则需要初始生命 3 。
但是如果继续走到格子(2, 2) ,那么最优方向一定是从 (1, 2) 过来(另一个方向负数太多)。但是到 (1, 2)的最优路线保存的是 下 -> 右 -> 右 这一条,走到终点总和是 -4 ,初始所需最小生命增大为 5 。而另一条原本不怎么好的路线 右 -> 右 -> 下 总和是 -2 ,初始所需最小生命 3 ,所以仍然保持不变。
这样看来原本不好的路线在最后的结果里是可能会变好的,因此不好保存下来直接递推。那怎么办呢?
还记得以前我们公众号分享过一个动态规划的通解(公众号后台返回“动态规划”可得),其中构建dp数组的目标,就是让这个dp数组能直接返回答案。所以,本题我们构建的dp数组,存放的就是还未经过当前格子时,保证骑士经过这个格子而不死的最低健康数,那么我们就应该从后往前来填充这个dp数组了。
【举例】
拿此图举例,从终点开始,dp数组应该初始化为下图,因为(3,3)要扣5点血,所以还未经过当前格子时,保证骑士经过这个格子而不死的最低健康数为6
| 0(K) | 0 | 0 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 0 | 6(P) |
第二步就是初始化边界,如下图。这里要注意的是,骑士的血最少必须保证为1,不然就死了。
| 0(K) | 0 | 2 |
|---|---|---|
| 0 | 0 | 5 |
| 1 | 1 | 6(P) |
最后,我们的状态转移方程为:
int minNum = Math.min(dp[i+1][j],dp[i][j+1]);
dp[i][j] = Math.max(minNum-dungeon[i][j],1);
填满整个格子如下,最终返回dp[0][0]
| 7(K) | 5 | 2 |
|---|---|---|
| 6 | 11 | 5 |
| 1 | 1 | 6(P) |
【代码】
class Solution {
public int calculateMinimumHP(int[][] dungeon) {
int n = dungeon.length, m = dungeon[0].length;
int[][] dp = new int[n][m];
dp[n-1][m-1] = (-1)*Math.min(0, dungeon[n-1][m-1])+1;
if(n==1 && m==1)
return dp[n-1][m-1];
for(int i=n-2;i>=0;i--)
dp[i][m-1] = Math.max(dp[i+1][m-1]-dungeon[i][m-1],1);
for(int i=m-2;i>=0;i--)
dp[n-1][i] = Math.max(dp[n-1][i+1]-dungeon[n-1][i],1);
for(int i=n-2;i>=0;i--){
for(int j=m-2;j>=0;j--){
int minNum = Math.min(dp[i+1][j],dp[i][j+1]);
dp[i][j] = Math.max(minNum-dungeon[i][j],1);
}
}
return dp[0][0];
}
}
拜托点一个在看吧 >_<
来个直击灵魂的三连吧!
