动画 | 什么是红黑树?(与2-3-4树等价)
来源：算法无遗策
作者：我脱下短袖
二分搜索树是为了快速查找而生，它是一颗二叉树，每一个节点只有一个元素（值或键值对），左子树所有节点的值均小于父节点的值，右子树所有的值均大于父节点的值，左右子树也是一颗二分搜索树，而且没有键值相等的节点。它的查找、插入和删除的时间复杂度都与树高成比例，期望值是O(logn)。
但是插入数组如[15，17，13，12，9，7]，二分搜索树就暴露了缺点，将树退化成线性表，查找的时间复杂度达到最坏时间复杂度O(n)。 动画：二分搜索树退化成线性表
那有没有插入和删除操作都能保持树的完美平衡性（任何一个节点到其叶子节点的路径长度都是相等的）？ 有，B树。B树是一种自平衡的树，根节点到其叶子节点的路径高度都是一样的，能够保持数据有序（通过中序遍历能得到有序数据）。B树一个节点可以拥有2个以上的子树，如2-3树、2-3-4树甚至2-3-4-5-6-7-8树，它们满足二分搜索树的性质，但它们不属于二叉树，也不属于二分搜索树。 2-3-4树的完美平衡，每条从根节点到叶子节点的路径的高度都是一样的 2-3-4树有以下节点组成： 2-节点，含有一个元素（值或键值对）和两个子树（左右子树），左子树所有的值均小于父节点的值，右子树所有的值均大于父节点的值； 3-节点，含有两个元素和三个子树，左子树所有的值均小于父节点最小元素的值，中间子树所有的值均位于父节点两个元素之间，右子树所有的值均大于父节点最大元素的值； 4-节点，含有三个元素和四个子树，节点之间的比较也满足二分搜索树的性质。 2-3-4树查找算法 2-3-4树的查找类似二分搜索树的查找。 2-3-4树插入算法 2-3-4树的插入算法是消除当前节点是4-节点，将4-节点分解成多个2-节点，中间的2-节点与父节点合并成3-节点或4-节点。 沿着链接向下进行变换分解4-节点分为两种情况： 1）4-节点作为根节点，分解成3个2-节点，中间的2-节点作为根节点； 2）当前节点为4-节点，分解成3个2-节点，中间的2-节点与父节点合并成3-节点或4-节点；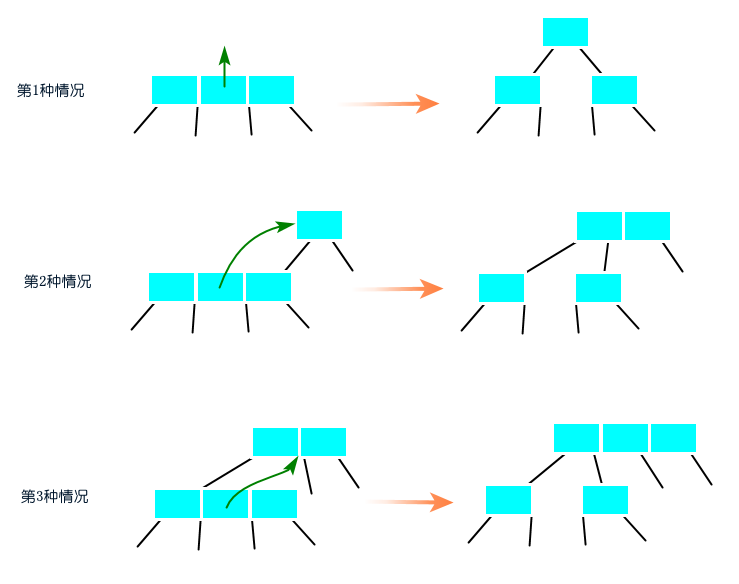
图：沿着链接向下进行变换，分解4-节点 在沿着左右链接向下进行变换的同时，也会进行命中查找。如果元素是键值对的话，查找命中将旧的值赋值为新的值；如果元素是一个值的话，查找命中将忽略之，因为二分搜索树需要满足没有相等的元素；如果需要支持重复的元素，则在元素对象添加count属性，默认为1。 如果查找未命中，则将待插入元素插入在叶子节点上。树底下插入一个元素只有两种情况：向2-节点中插入和向3-节点中插入。 
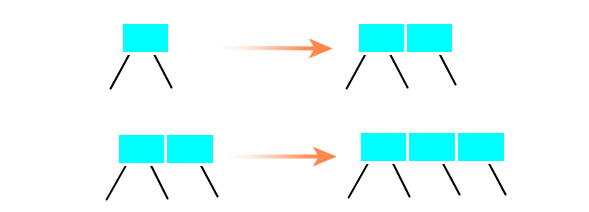图：树底下插入一个元素 2-3-4树删除算法 2-3-4树的删除算法是消除当前节点是2-节点，向兄弟节点或父节点借一个元素过来。 删除最小元素 从根节点的左孩子开始，沿着左链接向下进行变换可以分为三种情况： 1）当前节点不是2-节点，跳过； 2）当前节点是2-节点，兄弟节点是2-节点，将当前节点、父节点最小元素和兄弟节点合并为4-节点，当前节点变换成4-节点； 3）当前节点是2-节点，兄弟节点不是2-节点，将兄弟节点的最小元素移到父节点，父节点的最小元素移到当前节点，当前节点变换成3-节点。 
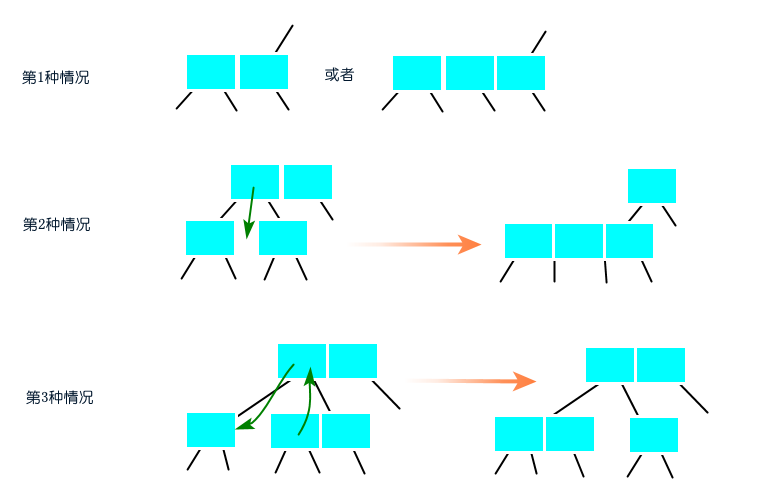图：沿着左链接向下进行变换 删除最大元素 从根节点的右孩子开始，沿着右链接向下进行变换也同样分为三种情况： 1）当前节点不是2-节点，跳过； 2）当前节点是2-节点，兄弟节点是2-节点，将当前节点、父节点的最大元素和兄弟节点合并为4-节点，当前节点变换成4-节点； 3）当前节点是2-节点，兄弟节点不是2-节点，将兄弟节点的最大元素移到父节点，父节点的最大元素移到当前节点，当前节点变换成3-节点。 
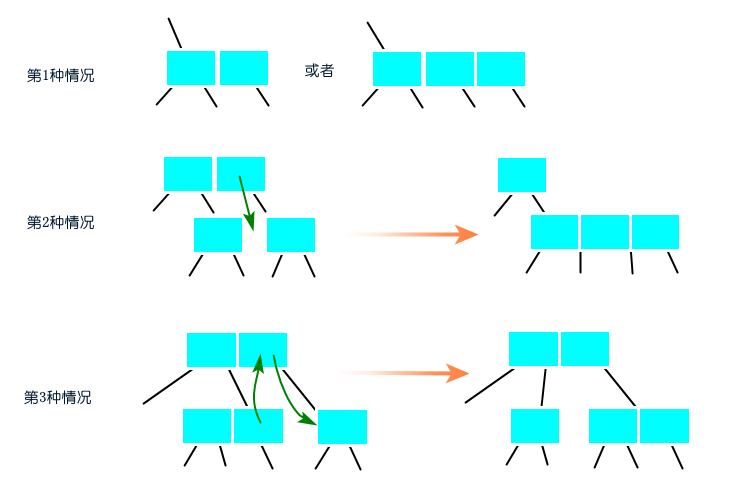图：沿着右链接向下进行变换 删除任意元素 学习过删除最小元素和删除最大元素算法之后，删除任意元素的算法自然就简单了。删除任意元素算法需要先进行命中查找，若查找命中，则将右子树的最小值替换掉待删除元素，然后将右子树进行删除最小元素的算法。 2-3-4树虽满足二分搜索树的性质，但不是一颗二分搜索树。如果期望它是一颗二分搜索树，就需要将3-节点和4-节点替换为多个2-节点，还需要注明元素之间的关系（用红链接表示）。 替换3-节点和4-节点 
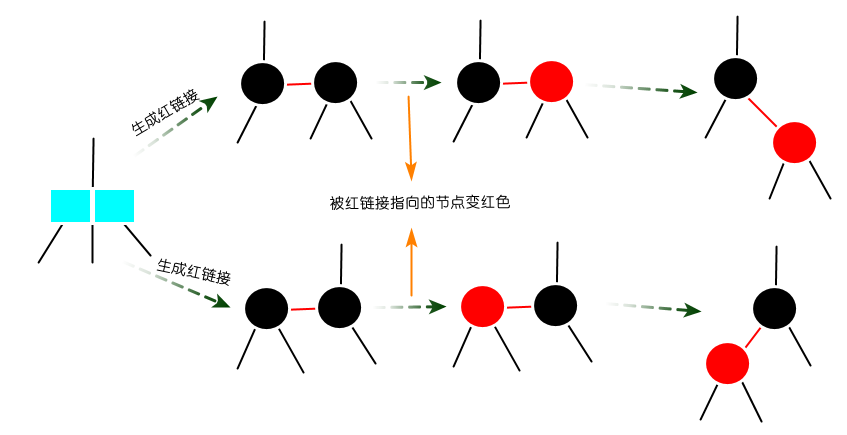图：替换3-节点 
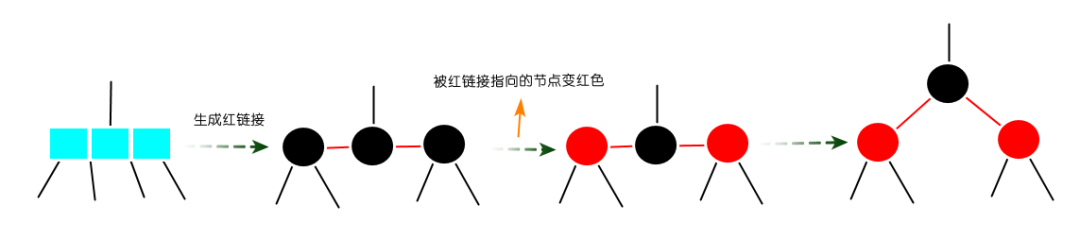图：替换4-节点 但是存在一个问题，2-3-4树因为3-节点的不同表示会有很多种不同的红黑树，3-节点既可以左倾，也可以右倾。所以为了保证树的唯一性，3-节点只考虑左倾，当然你也可以只考虑右倾。 这样对于任何一颗2-3-4树，只考虑左倾的情况下，都能得到唯一的一颗对应的红黑树，这种树也叫左倾红黑树，相对比较减少了复杂性，设计更容易被实现。 红黑树查找算法 红黑树的查找算法和二分搜索树一样。 关于链接的颜色变换只跟颜色转换有关，而旋转不会改变链接的颜色变换，只在被红链接指向的节点变成红色，被黑链接指向的节点变成黑色。 旋转 旋转是将不满足红黑树性质的3-节点和4-节点进行旋转，如果3-节点出现右链接，则将右链接通过左旋转变成左链接；如果4-节点出现一个红节点连着两条红链接，则将4-节点配平。 左旋转 
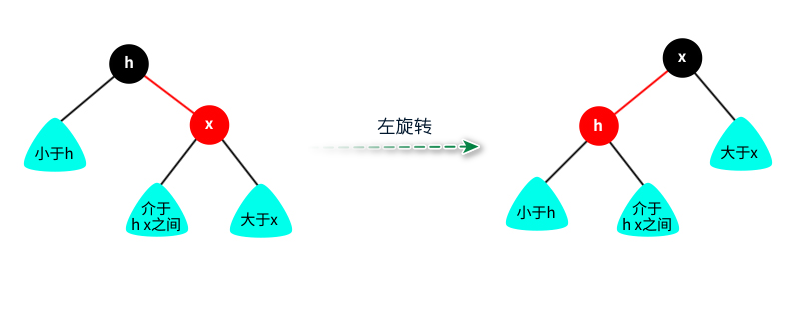图：左旋转 右旋转 
图：右旋转 
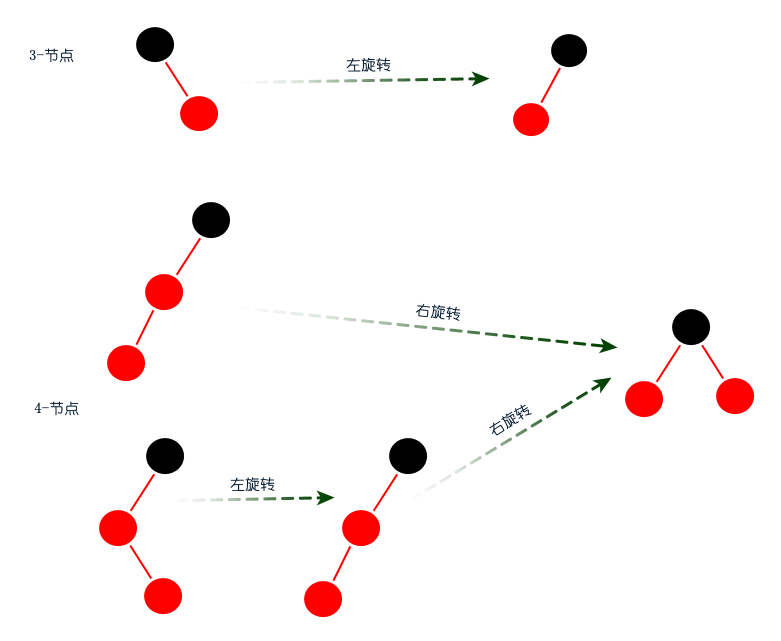图：3-节点和4-节点的旋转 Code：右旋转和左旋转 
颜色转换 颜色转换只应用于4-节点。 
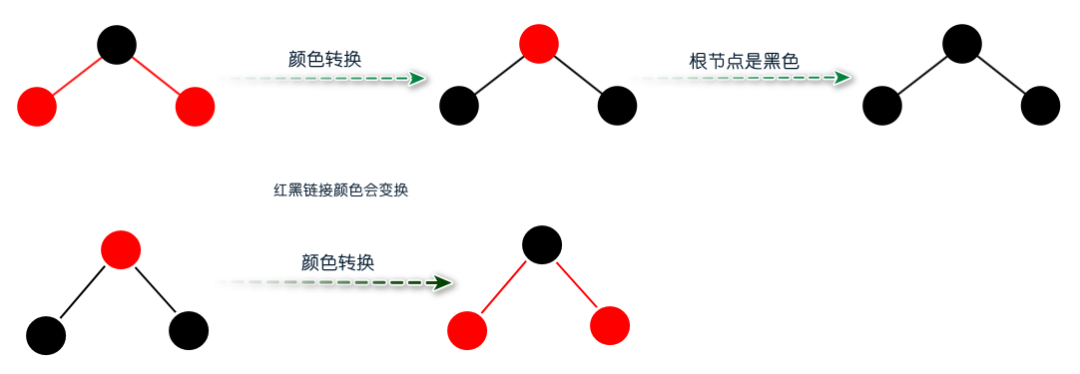图：颜色转换 Code：颜色转换 
红黑树插入算法 回顾之前的2-3-4树的插入算法，它有两个过程：沿着链接向下进行分解4-节点和树底下插入一个元素。 红黑树的插入算法和2-3-4树的插入算法类似，它不仅包含前面两个过程，还增加了向上进行变换的过程，此过程是将3-节点左倾和4-节点配平。 红黑树插入算法会先从根节点开始，沿着左右链接向下进行变换，目的是为了分解4-节点。如果该节点的左右孩子都是红节点，则通过flipColors方法进行颜色转换，接着进行下一个子节点；如果不是，则直接进行下一个子节点。 到达树底的时候，则意味着可以开始插入新的元素。 如果红黑树目前是一颗空树，插入红色的元素作为第一个节点，然后该节点变成黑色。如果不是一颗空树，插入元素分为三种情况：向2-节点插入新元素、向3-节点插入新元素和向4-节点插入新元素。 向2-节点插入新元素 向2-节点插入新元素很简单，如果新元素的值小于父节点，直接插入红色的节点即可；如果新元素的值大于父节点，则产生一个红色右链接，插完之后则将3-节点进行左旋转，将右链接变成左链接，被红链接指向的节点变成红色，被黑链接指向的节点变成黑色。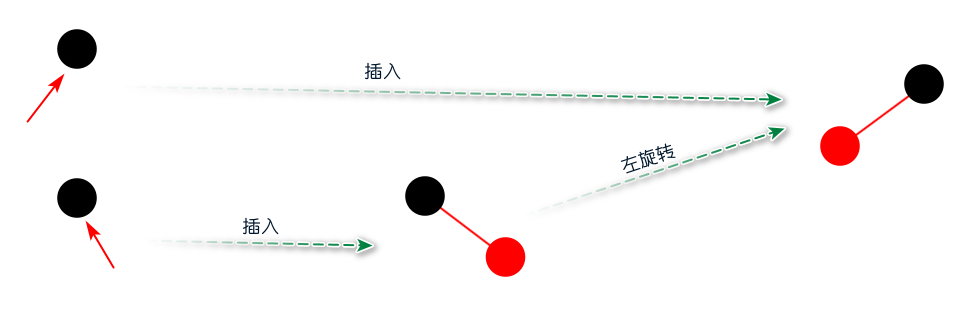 
图：向2-节点插入新元素 向3-节点插入新元素 因为前面的3-节点进行过旋转，此时的3-节点肯定满足左倾红黑树的性质。向3-节点插入新元素分为三种情况： 1）新元素的值位于3-节点中的两元素之间； 2）新元素的值小于3-节点中的最小元素； 3）新元素的值大于3-节点中的最大元素。 
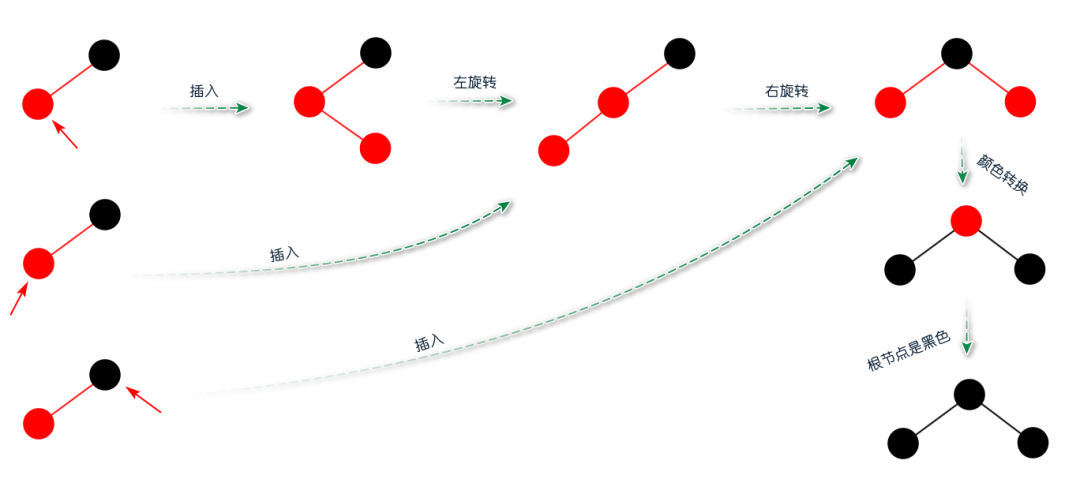图：向3-节点插入新元素 向4-节点插入新元素 向4-节点插入新元素之前需要先进行颜色转换，才可以进行插入新的元素。 
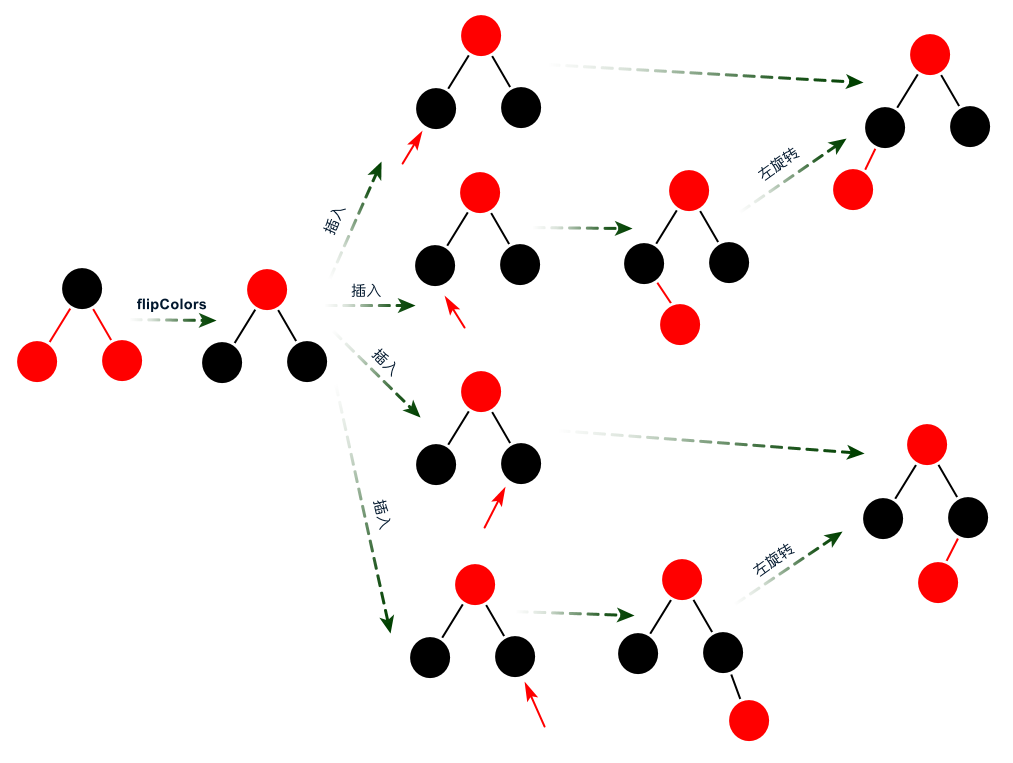图：向4-节点插入新元素 插完新元素之后需要满足红黑树的性质，则在沿着父节点的链接向上进行变换，具体做法和向3-节点插入新元素的做法类似，通过左旋转将3-节点左倾和左右旋转将4-节点配平，没有颜色转换。 动画：2-3-4树与红黑树的插入
Code：红黑树插入算法
红黑树删除算法 红黑树删除算法也需要进行旋转和颜色转换操作，在插入算法中为了待插入元素所在的节点不是4-节点，所以在沿着左右链接向下进行变换时将4-节点分解成3个2-节点，中间的2-节点与父节点合并；而在删除算法中为了待删除元素所在的节点不是2-节点，所以在沿着左右链接向下进行变换时将2-节点向其它不是2-节点的节点（兄弟节点或父节点）借一个元素过来，合并成3-节点。 所以，只要是2-节点的节点，如果兄弟节点不是2-节点，就将兄弟节点的与父节点邻近的元素移到父节点，而父节点将与当前节点邻近的元素移到当前节点；如果兄弟节点是2-节点，则将父节点的与当前节点邻近的元素移到当前节点。（是不是很绕？待会在后面删除最值算法中详细给出） 然后删除完一个元素之后需要进行修复调整，将这个树满足红黑树的性质。如果右链接是红色，将右链接通过左旋转变成左链接；如果有连续的左链接，通过右旋转配平，然后进行颜色转换。 Code：向上变换（修复调整） 
删除最小元素 删除最小元素算法和二分搜索树一样，一直递归它的左孩子，直到它的左孩子为空才进行删除这个最小元素。但是红黑树在递归的同时如何旋转和颜色转换是个问题。 删除最小元素算法一直沿着左链接向下进行转换，对照2-3-4树，我们可以给出三种情况，从根节点开始： 1）当前节点（父节点位置）的左子节点不是2-节点，直接进行下一个节点（左子节点）； 2）当前节点的左子节点和右子节点都是2-节点，则将左子节点、当前节点的最小元素和右子节点合并成4-节点，然后进行下一个节点； 3）当前节点的左子节点是2-节点，右子节点不是2-节点，则将右子节点的最小元素移到当前节点的位置，当前节点的最小元素移到左子节点，然后进行下一个节点。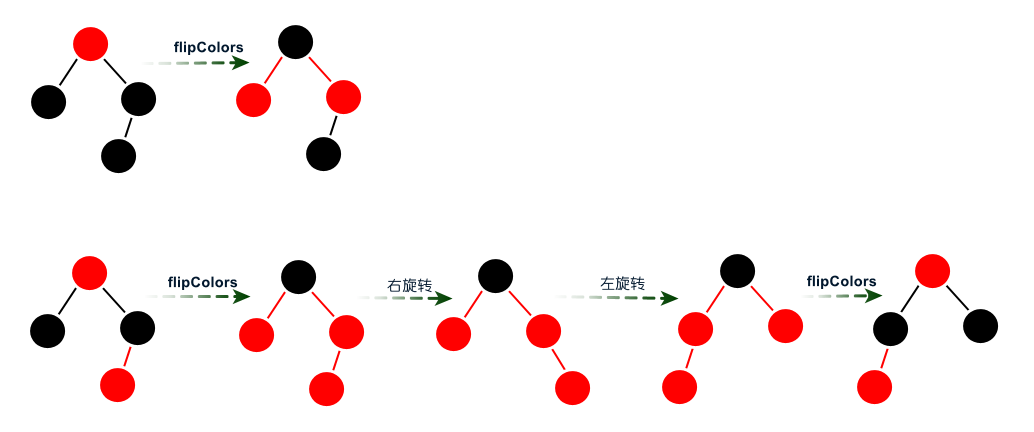 
图：沿着左链接向下进行转换 Code：沿着左链接向下变换 
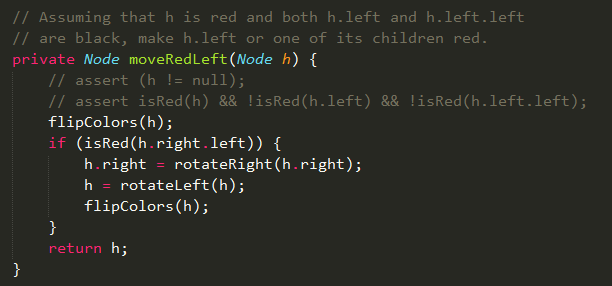直到某元素左孩子为空的时候，此时的元素是这个树的最小元素。因为通过前面的转换，最小元素肯定被一个红链接指向，删除这个元素之后通过balance方法修复调整为红黑树。 Code：删除最小元素算法 
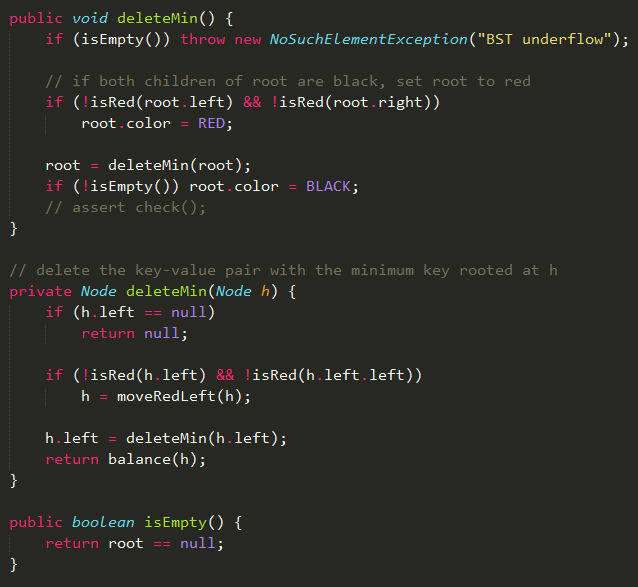删除最大元素 删除最大元素算法和删除最小元素算法类似的，也分为三种情况： 1）当前节点（父节点位置）的右子节点不是2-节点，直接进行下一个节点（右子节点）； 2）当前节点的右子节点和左子节点都是2-节点，则将右子节点、当前节点的最大元素和左子节点合并成4-节点，然后进行下一个节点； 3）当前节点的右子节点是2-节点，左子节点不是2-节点，则将左子节点的最大元素移到当前节点的位置，当前节点的最大元素移到左子节点，然后进行下一个节点。 
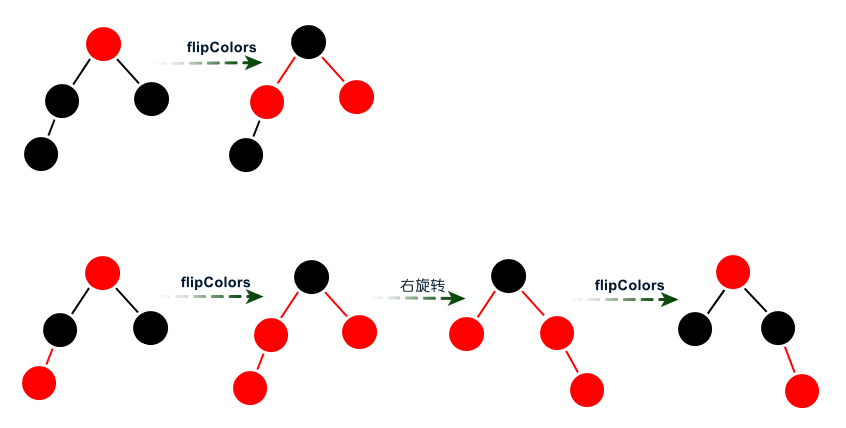图：沿着右链接向下进行变换 Code：沿着右链接向下变换 
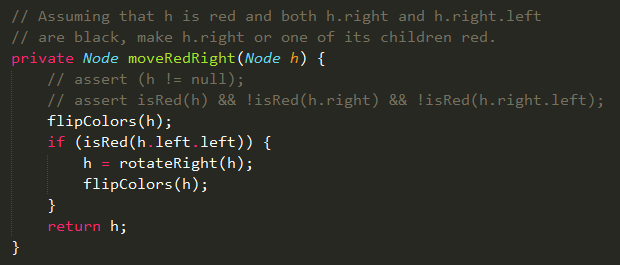Code：删除最大元素算法 
删除任意元素 学习过前面的删除最小元素算法和删除最大元素算法，删除任意元素会变得很简单。删除最小元素算法会一直沿着左链接向下进行变换，删除最大元素算法会一直沿着右链接向下进行变换，而删除任意元素算法需要同时存在着左右链接向下进行变换。 删除任意元素算法需要先进行命中查找，在命中查找的过程中会进行沿着左右链接向下变换，如果查找命中则将右子树的最小元素替换掉待删除元素，然后进行右子树的删除最小元素算法；如果查找未命中，则直接返回balance函数，向上将3-节点左倾或将4-节点配平。 Code：删除任意元素算法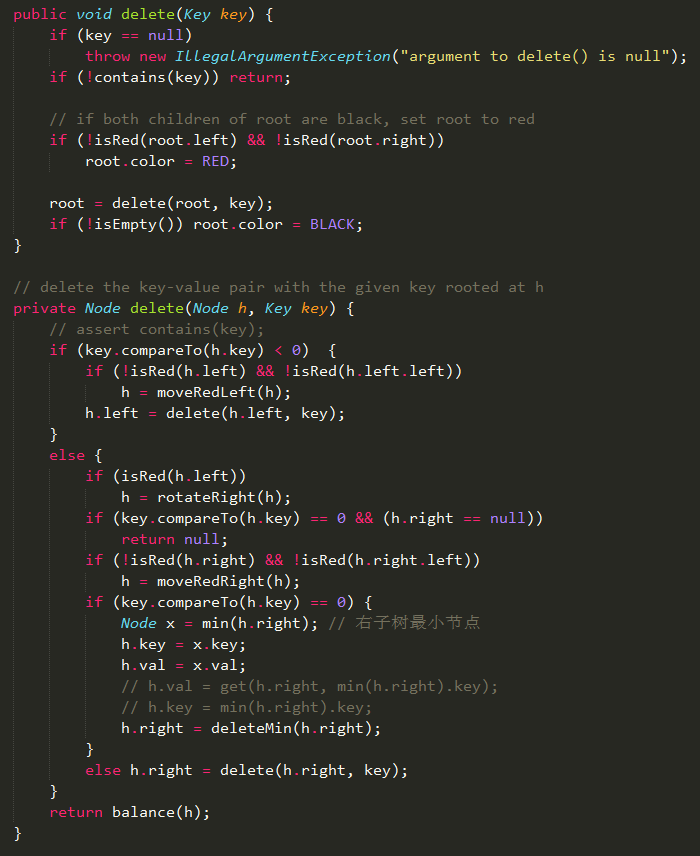 
动画：2-3-4树与红黑树的删除
学习完上面的算法之后，可以总结下红黑树的性质： 1）每个节点或是红色的，或是黑色的； 2）根节点是黑色的； 3）每个叶子节点（NIL）是黑色的； 4）如果一个节点是红色的，则它的两个子节点都是黑色的（NIL节点也是黑色的）； 5）对每个结点，从该节点到其所有后代叶子节点的简单路径上，均包含相同数目的黑色节点（黑链接平衡）。
作者：我脱下短袖
二分搜索树是为了快速查找而生，它是一颗二叉树，每一个节点只有一个元素（值或键值对），左子树所有节点的值均小于父节点的值，右子树所有的值均大于父节点的值，左右子树也是一颗二分搜索树，而且没有键值相等的节点。它的查找、插入和删除的时间复杂度都与树高成比例，期望值是O(logn)。
但是插入数组如[15，17，13，12，9，7]，二分搜索树就暴露了缺点，将树退化成线性表，查找的时间复杂度达到最坏时间复杂度O(n)。 动画：二分搜索树退化成线性表
那有没有插入和删除操作都能保持树的完美平衡性（任何一个节点到其叶子节点的路径长度都是相等的）？ 有，B树。B树是一种自平衡的树，根节点到其叶子节点的路径高度都是一样的，能够保持数据有序（通过中序遍历能得到有序数据）。B树一个节点可以拥有2个以上的子树，如2-3树、2-3-4树甚至2-3-4-5-6-7-8树，它们满足二分搜索树的性质，但它们不属于二叉树，也不属于二分搜索树。 2-3-4树的完美平衡，每条从根节点到叶子节点的路径的高度都是一样的 2-3-4树有以下节点组成： 2-节点，含有一个元素（值或键值对）和两个子树（左右子树），左子树所有的值均小于父节点的值，右子树所有的值均大于父节点的值； 3-节点，含有两个元素和三个子树，左子树所有的值均小于父节点最小元素的值，中间子树所有的值均位于父节点两个元素之间，右子树所有的值均大于父节点最大元素的值； 4-节点，含有三个元素和四个子树，节点之间的比较也满足二分搜索树的性质。 2-3-4树查找算法 2-3-4树的查找类似二分搜索树的查找。 2-3-4树插入算法 2-3-4树的插入算法是消除当前节点是4-节点，将4-节点分解成多个2-节点，中间的2-节点与父节点合并成3-节点或4-节点。 沿着链接向下进行变换分解4-节点分为两种情况： 1）4-节点作为根节点，分解成3个2-节点，中间的2-节点作为根节点； 2）当前节点为4-节点，分解成3个2-节点，中间的2-节点与父节点合并成3-节点或4-节点；
图：沿着链接向下进行变换，分解4-节点 在沿着左右链接向下进行变换的同时，也会进行命中查找。如果元素是键值对的话，查找命中将旧的值赋值为新的值；如果元素是一个值的话，查找命中将忽略之，因为二分搜索树需要满足没有相等的元素；如果需要支持重复的元素，则在元素对象添加count属性，默认为1。 如果查找未命中，则将待插入元素插入在叶子节点上。树底下插入一个元素只有两种情况：向2-节点中插入和向3-节点中插入。 图：树底下插入一个元素 2-3-4树删除算法 2-3-4树的删除算法是消除当前节点是2-节点，向兄弟节点或父节点借一个元素过来。 删除最小元素 从根节点的左孩子开始，沿着左链接向下进行变换可以分为三种情况： 1）当前节点不是2-节点，跳过； 2）当前节点是2-节点，兄弟节点是2-节点，将当前节点、父节点最小元素和兄弟节点合并为4-节点，当前节点变换成4-节点； 3）当前节点是2-节点，兄弟节点不是2-节点，将兄弟节点的最小元素移到父节点，父节点的最小元素移到当前节点，当前节点变换成3-节点。 图：沿着左链接向下进行变换 删除最大元素 从根节点的右孩子开始，沿着右链接向下进行变换也同样分为三种情况： 1）当前节点不是2-节点，跳过； 2）当前节点是2-节点，兄弟节点是2-节点，将当前节点、父节点的最大元素和兄弟节点合并为4-节点，当前节点变换成4-节点； 3）当前节点是2-节点，兄弟节点不是2-节点，将兄弟节点的最大元素移到父节点，父节点的最大元素移到当前节点，当前节点变换成3-节点。 图：沿着右链接向下进行变换 删除任意元素 学习过删除最小元素和删除最大元素算法之后，删除任意元素的算法自然就简单了。删除任意元素算法需要先进行命中查找，若查找命中，则将右子树的最小值替换掉待删除元素，然后将右子树进行删除最小元素的算法。 2-3-4树虽满足二分搜索树的性质，但不是一颗二分搜索树。如果期望它是一颗二分搜索树，就需要将3-节点和4-节点替换为多个2-节点，还需要注明元素之间的关系（用红链接表示）。 替换3-节点和4-节点 图：替换3-节点 图：替换4-节点 但是存在一个问题，2-3-4树因为3-节点的不同表示会有很多种不同的红黑树，3-节点既可以左倾，也可以右倾。所以为了保证树的唯一性，3-节点只考虑左倾，当然你也可以只考虑右倾。 这样对于任何一颗2-3-4树，只考虑左倾的情况下，都能得到唯一的一颗对应的红黑树，这种树也叫左倾红黑树，相对比较减少了复杂性，设计更容易被实现。 红黑树查找算法 红黑树的查找算法和二分搜索树一样。 关于链接的颜色变换只跟颜色转换有关，而旋转不会改变链接的颜色变换，只在被红链接指向的节点变成红色，被黑链接指向的节点变成黑色。 旋转 旋转是将不满足红黑树性质的3-节点和4-节点进行旋转，如果3-节点出现右链接，则将右链接通过左旋转变成左链接；如果4-节点出现一个红节点连着两条红链接，则将4-节点配平。 左旋转 图：左旋转 右旋转 图：右旋转 图：3-节点和4-节点的旋转 Code：右旋转和左旋转 颜色转换 颜色转换只应用于4-节点。 图：颜色转换 Code：颜色转换 红黑树插入算法 回顾之前的2-3-4树的插入算法，它有两个过程：沿着链接向下进行分解4-节点和树底下插入一个元素。 红黑树的插入算法和2-3-4树的插入算法类似，它不仅包含前面两个过程，还增加了向上进行变换的过程，此过程是将3-节点左倾和4-节点配平。 红黑树插入算法会先从根节点开始，沿着左右链接向下进行变换，目的是为了分解4-节点。如果该节点的左右孩子都是红节点，则通过flipColors方法进行颜色转换，接着进行下一个子节点；如果不是，则直接进行下一个子节点。 到达树底的时候，则意味着可以开始插入新的元素。 如果红黑树目前是一颗空树，插入红色的元素作为第一个节点，然后该节点变成黑色。如果不是一颗空树，插入元素分为三种情况：向2-节点插入新元素、向3-节点插入新元素和向4-节点插入新元素。 向2-节点插入新元素 向2-节点插入新元素很简单，如果新元素的值小于父节点，直接插入红色的节点即可；如果新元素的值大于父节点，则产生一个红色右链接，插完之后则将3-节点进行左旋转，将右链接变成左链接，被红链接指向的节点变成红色，被黑链接指向的节点变成黑色。 图：向2-节点插入新元素 向3-节点插入新元素 因为前面的3-节点进行过旋转，此时的3-节点肯定满足左倾红黑树的性质。向3-节点插入新元素分为三种情况： 1）新元素的值位于3-节点中的两元素之间； 2）新元素的值小于3-节点中的最小元素； 3）新元素的值大于3-节点中的最大元素。 图：向3-节点插入新元素 向4-节点插入新元素 向4-节点插入新元素之前需要先进行颜色转换，才可以进行插入新的元素。 图：向4-节点插入新元素 插完新元素之后需要满足红黑树的性质，则在沿着父节点的链接向上进行变换，具体做法和向3-节点插入新元素的做法类似，通过左旋转将3-节点左倾和左右旋转将4-节点配平，没有颜色转换。 动画：2-3-4树与红黑树的插入 Code：红黑树插入算法
红黑树删除算法 红黑树删除算法也需要进行旋转和颜色转换操作，在插入算法中为了待插入元素所在的节点不是4-节点，所以在沿着左右链接向下进行变换时将4-节点分解成3个2-节点，中间的2-节点与父节点合并；而在删除算法中为了待删除元素所在的节点不是2-节点，所以在沿着左右链接向下进行变换时将2-节点向其它不是2-节点的节点（兄弟节点或父节点）借一个元素过来，合并成3-节点。 所以，只要是2-节点的节点，如果兄弟节点不是2-节点，就将兄弟节点的与父节点邻近的元素移到父节点，而父节点将与当前节点邻近的元素移到当前节点；如果兄弟节点是2-节点，则将父节点的与当前节点邻近的元素移到当前节点。（是不是很绕？待会在后面删除最值算法中详细给出） 然后删除完一个元素之后需要进行修复调整，将这个树满足红黑树的性质。如果右链接是红色，将右链接通过左旋转变成左链接；如果有连续的左链接，通过右旋转配平，然后进行颜色转换。 Code：向上变换（修复调整） 删除最小元素 删除最小元素算法和二分搜索树一样，一直递归它的左孩子，直到它的左孩子为空才进行删除这个最小元素。但是红黑树在递归的同时如何旋转和颜色转换是个问题。 删除最小元素算法一直沿着左链接向下进行转换，对照2-3-4树，我们可以给出三种情况，从根节点开始： 1）当前节点（父节点位置）的左子节点不是2-节点，直接进行下一个节点（左子节点）； 2）当前节点的左子节点和右子节点都是2-节点，则将左子节点、当前节点的最小元素和右子节点合并成4-节点，然后进行下一个节点； 3）当前节点的左子节点是2-节点，右子节点不是2-节点，则将右子节点的最小元素移到当前节点的位置，当前节点的最小元素移到左子节点，然后进行下一个节点。 图：沿着左链接向下进行转换 Code：沿着左链接向下变换 直到某元素左孩子为空的时候，此时的元素是这个树的最小元素。因为通过前面的转换，最小元素肯定被一个红链接指向，删除这个元素之后通过balance方法修复调整为红黑树。 Code：删除最小元素算法 删除最大元素 删除最大元素算法和删除最小元素算法类似的，也分为三种情况： 1）当前节点（父节点位置）的右子节点不是2-节点，直接进行下一个节点（右子节点）； 2）当前节点的右子节点和左子节点都是2-节点，则将右子节点、当前节点的最大元素和左子节点合并成4-节点，然后进行下一个节点； 3）当前节点的右子节点是2-节点，左子节点不是2-节点，则将左子节点的最大元素移到当前节点的位置，当前节点的最大元素移到左子节点，然后进行下一个节点。 图：沿着右链接向下进行变换 Code：沿着右链接向下变换 Code：删除最大元素算法 删除任意元素 学习过前面的删除最小元素算法和删除最大元素算法，删除任意元素会变得很简单。删除最小元素算法会一直沿着左链接向下进行变换，删除最大元素算法会一直沿着右链接向下进行变换，而删除任意元素算法需要同时存在着左右链接向下进行变换。 删除任意元素算法需要先进行命中查找，在命中查找的过程中会进行沿着左右链接向下变换，如果查找命中则将右子树的最小元素替换掉待删除元素，然后进行右子树的删除最小元素算法；如果查找未命中，则直接返回balance函数，向上将3-节点左倾或将4-节点配平。 Code：删除任意元素算法 动画：2-3-4树与红黑树的删除 学习完上面的算法之后，可以总结下红黑树的性质： 1）每个节点或是红色的，或是黑色的； 2）根节点是黑色的； 3）每个叶子节点（NIL）是黑色的； 4）如果一个节点是红色的，则它的两个子节点都是黑色的（NIL节点也是黑色的）； 5）对每个结点，从该节点到其所有后代叶子节点的简单路径上，均包含相同数目的黑色节点（黑链接平衡）。
推荐阅读
评论