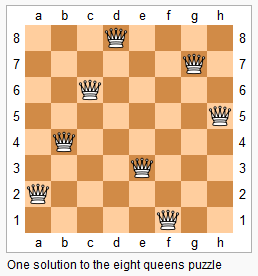
样例 输入: 4 2 4 皇后问题存在如下两个不同的解法。".Q.." , // 解法 1 "...Q" ,"Q..." ,"..Q." ],"..Q." , // 解法 2 "Q..." ,"...Q" ,".Q.." ]
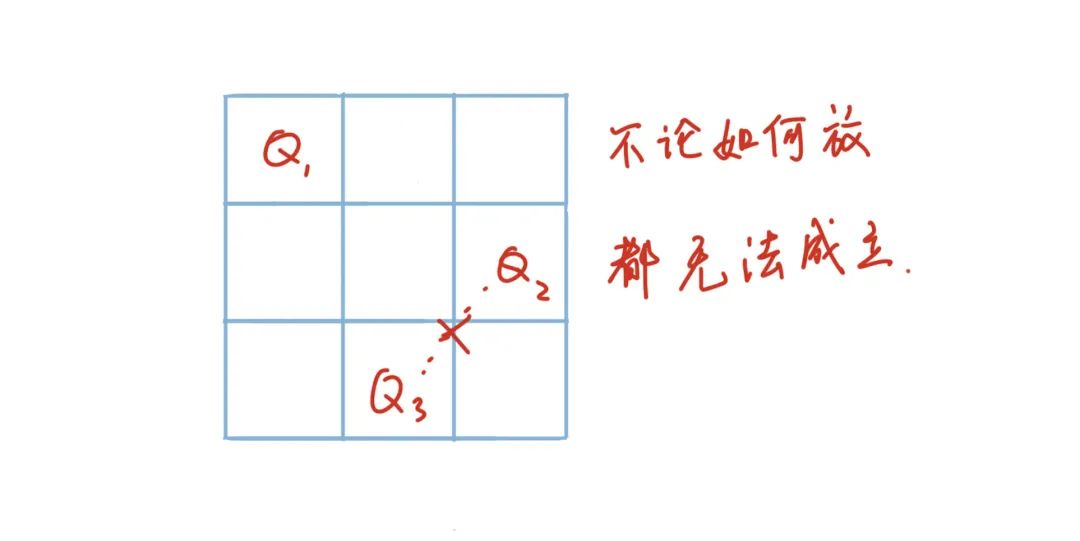
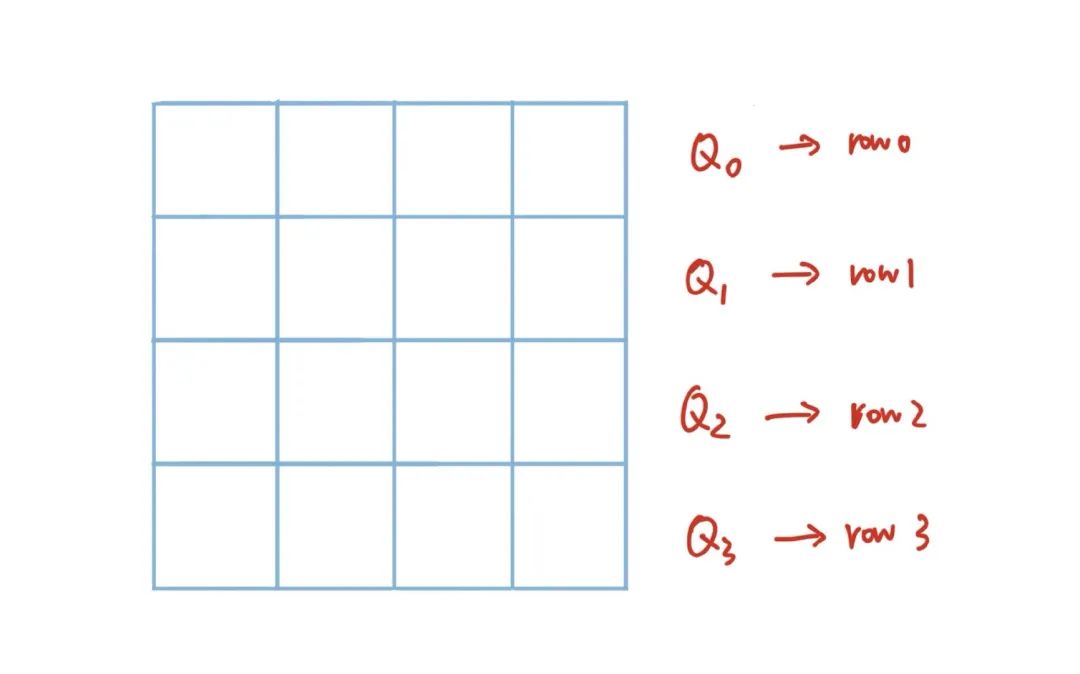
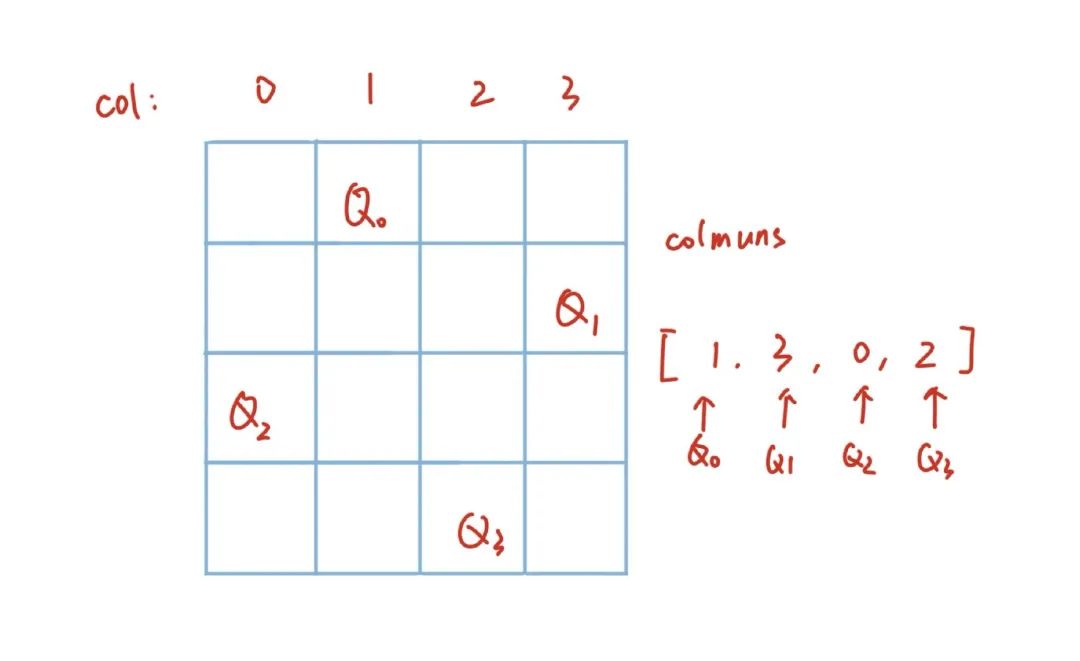
解题 https://www.cnblogs.com/techflow/p/12782020.html 思路分析 八皇后问题已经是老生常谈了,在我们探讨解法之前,先来思考一个问题,用递归或者搜索解决的问题很多,为什么只有N皇后问题如此经典呢? 是因为国际象棋比较流行吗?还是因为这个问题很困难吗?还是它的思路很巧妙吗?由于这个问题是我自己提出的,书本上并没有相关的答案,需要我们自己思考。我们先不公布答案,带着这个问题来分析一下这道题的思路。 我个人在解题的时候喜欢问问题,很多时候看似破朔迷离找不到头绪的题目,多问几个问题也许就能找到灵感 。如果我们对数字敏感的话,很容易发现一个大问题,为什么题目会让我们在n*n的棋盘上摆放n个皇后呢?为什么是n个,而不是2n个,也不是n+1个呢? 这个问题不难回答,因为题目当中规定了皇后不能同行摆放 ,所以每一行最多摆放一个皇后,一共有n行,那么显然最多只能摆放n个皇后。但是如果我们继续提问,既然这么多限制条件,那为什么一定能找到答案呢 ,会不会摆放n个皇后的解不存在呢?这当然是有可能的,我们很容易发现,当n=2和3的时候就没有解法。 如果我们顺着这个思路问下去,还可以挖掘出许多问题来。比如到底什么样的n可以使得一定有解呢?每一个n对应的解有没有规律呢?这样一直问下去,如果所有的问题都能解答,就说明这个问题就彻底吃透了。实际上这个问题背后是一个非常复杂的数学问题 ,会在之后开一篇文章单独讲解。 虽然不去深究这些问题,也一样可以把题目做出来,但很多时候思维和能力的差距就体现在这些看似无用的思考上。 我们先把问题简化,把解的存在性问题先放一放,既然题目要我们求,一定会给我们有解的n。而且我们也可以大概猜测得出结论,当n大于等于4的时候,N皇后问题一定有解。那么,我们怎么求解呢? 问题建模 我们干想是没有结果的,要对问题进行建模 。建模这个词很玄乎,听起来很高端,而且在很多场景当中都会出现。比如机器学习当中,我们需要建模,还有专门的数学建模大赛,但是少有人会对建模这个词进行解释。 经过了一系列思考,我个人总结,所谓的建模,其实就是一个寻找和设计适应问题的解法的过程 。模型就是从问题当中抽象出来的逻辑,比如N皇后摆放是问题本身,但是摆放的方法的逻辑才是模型。模型不是凭空出现的,是我们一点点构建的。这个过程有点像是搭积木,从无到有,从易到难,一点点将模型完善。 n*n的棋盘上摆放n个皇后,这个是问题本身,我们做第一层抽象。显然,由于皇后之间不能同行也不能同列,那么每一行和每一列只能摆放一个皇后。我们不能同时枚举一个皇后摆放的行和列,我们优先考虑其中的行。不如做一个假设,由于皇后之间没有差别,我们可以假设每一行摆放的皇后是固定的 。第一个皇后就摆放在第一行,第二个皇后就摆放在第二行。 进行了第一层抽象之后,问题清晰了许多,但是还是无法得出答案。所以我们还需要做第二层抽象和分析,每行固定一个皇后之后可以保证皇后之间不会同行发生冲突,但是不能保证不同列以及不同对角线。所以我们必须设计一个机制,来保证这一点。我们需要枚举皇后所有摆放的情况,所以不能再固定皇后摆放的列,既然不能固定,但是可以记录。由于我们已经确定了每一个皇后摆放的行,只要记录下它们摆放的列 ,就可以判断是否会构成同列以及同对角线。 到这里,我们已经找到解法了,但是我们还可以再做第三层抽象。由于皇后已经固定了行号,我们可以用数组当中的下标代替皇后 。下标0存储的位置就是皇后0摆放的列号,0就是皇后0的行号,那么我们用一个一维数组就存储了皇后摆放的二维信息。 也就是说我们在递归的时候,只用一个数组就记录了整个棋盘的情况,这个时候用代码实现起来就要容易很多。 # code for leetcode 51 class Solution def dfs (self , n, queen, ret) :if return for in # 如果同列 if in continue False # 判断是否存在同对角线 for in enumerate (queen):# len(queen)表示当前是第几个皇后 if abs (len(queen) - j) == abs (idx - i):True break if continue # 合法则放入i列 self .dfs(n, queen, ret)def transform (self , n, ret) :# 根据每个皇后摆放的列号还原棋盘 for in for in enumerate (arr):'.' for in 'Q' '' .join (row))return def solveNQueens (self , n: int) -> List [List [str]]:self .dfs(n, [], ret)return self .transform(n, ret)总结 最后,我们再回到一开始的问题,为什么递归求解的问题这么多,只有N皇后成为经典呢? 我觉得很重要的一个原因就在于这道题对应的建模过程 ,我们从无到有,抽丝剥茧,一点点将整个问题搭建起来,构建出了一个适配于当前问题的模型。并且经过我们的优化,这也是用递归实现的最佳模型。对于我们而言,把问题AC了其实并不重要,重要的是能够掌握这个思路构建的能力 ,这样以后我们就可以很方便地迁移到其他的问题场景当中,这才是学习的精髓。 好了,今天的文章就到这里,如果觉得有所收获,请顺手点个在看 或者转发吧,你们的支持是我最大的动力。