楼教主男人八题(第四题)
先讲几句,上周五开始,一直在头晕,稍微一动就感觉双脚离地了。

去医院检查了下,万幸只是过度疲劳。在家静养了一周,吃了些药,感觉又能卷起来了。不过还是友提下,身体才是革命的本钱,老铁们一定要好好保护身体呀~

接下来继续战斗~

开搞 1740 「A New Stone Game」。
题目链接
http://poj.org/problem?id=1740
题目描述
Alice and Bob decide to play a new stone game.At the beginning of the game they pick n(1<=n<=10) piles of stones in a line. Alice and Bob move the stones in turn.
At each step of the game,the player choose a pile,remove at least one stones,then freely move stones from this pile to any other pile that still has stones.
For example: n=4 and the piles have (3,1,4,2) stones.
If the player chose the first pile and remove one.Then it can reach the follow states.
2 1 4 2 1 2 4 2(move one stone to Pile 2) 1 1 5 2(move one stone to Pile 3) 1 1 4 3(move one stone to Pile 4) 0 2 5 2(move one stone to Pile 2 and another one to Pile 3) 0 2 4 3(move one stone to Pile 2 and another one to Pile 4) 0 1 5 3(move one stone to Pile 3 and another one to Pile 4) 0 3 4 2(move two stones to Pile 2) 0 1 6 2(move two stones to Pile 3) 0 1 4 4(move two stones to Pile 4)
Alice always moves first. Suppose that both Alice and Bob do their best in the game.
You are to write a program to determine who will finally win the game.
输入
The input contains several test cases.
The first line of each test case contains an integer number n, denoting the number of piles.
The following n integers describe the number of stones in each pile at the beginning of the game, you may assume the number of stones in each pile will not exceed 100.
The last test case is followed by one zero.
输出
For each test case, if Alice win the game,output 1,otherwise output 0.
样例输入
3
2 1 3
2
1 1
0
样例输出
1
0
题解
先来分析下选手可以做的操作,大体可以分为三个步骤:
从 n 堆石子中选中一堆,不妨记为 。 从 中取走 个,。 从剩余的 中取走 个,放入其他「尚未取完的」任意一堆或多堆,。
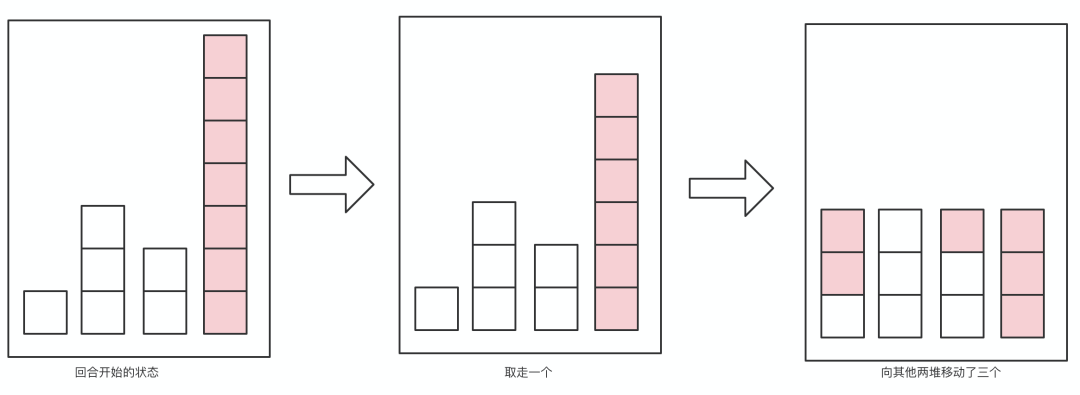
不难发现,当仅剩一堆石子时,选手可将石子全部取走,所以 是必胜局面。
接下来分析 的局面,当两堆数量相同时,先手只能让其中一堆减少,让另一堆数量增加或不变。
不妨假设先手让 减少了 个, 增加了 个。那么后手必然在 中取走 个,让两堆再次进入相等的局面。
直到先手进入 , 的局面,先手只能取完其中一堆,让后手进入 的必胜局面。
所以, 且两堆石子数量相同是必败局面。
当两堆石子不相等时,不妨设 ,先手总是可以在 中取走 个,让后手进入必败局面。
所以, 且两堆石子数量不相同是必胜局面。
继续发散,考虑到 是偶数时,如果任意一堆都存在另一堆数量和它相同。比如像下面这样:
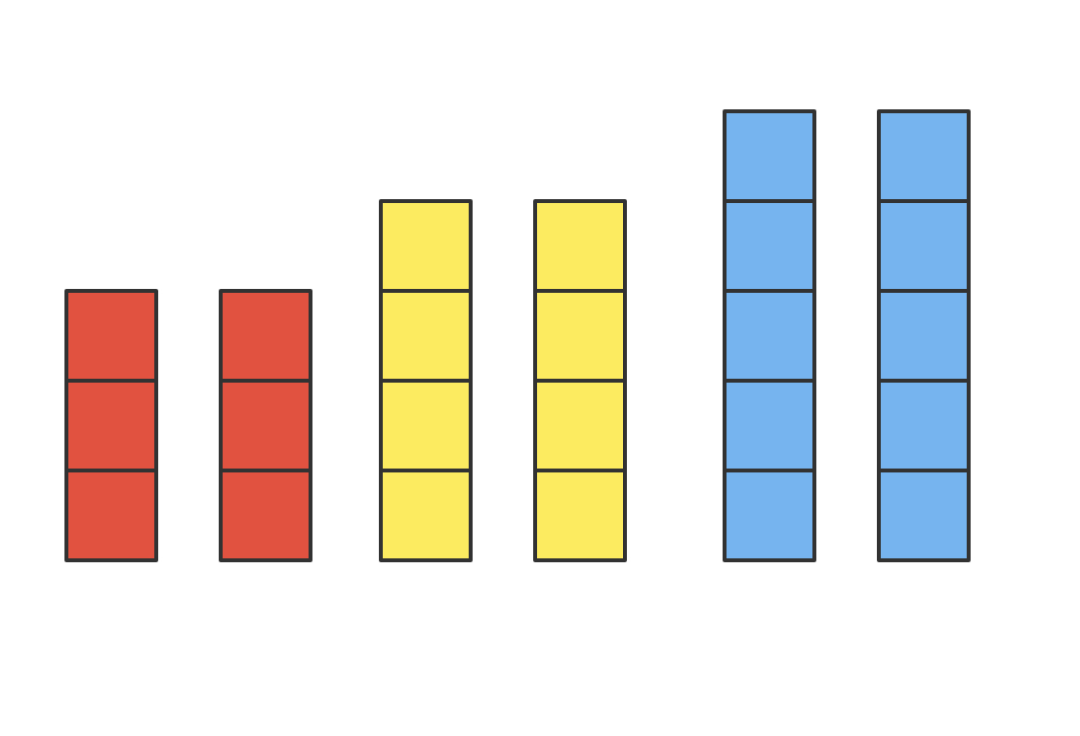
这时,可以将这 堆石子,分成完全相同的两部分,比如这样:
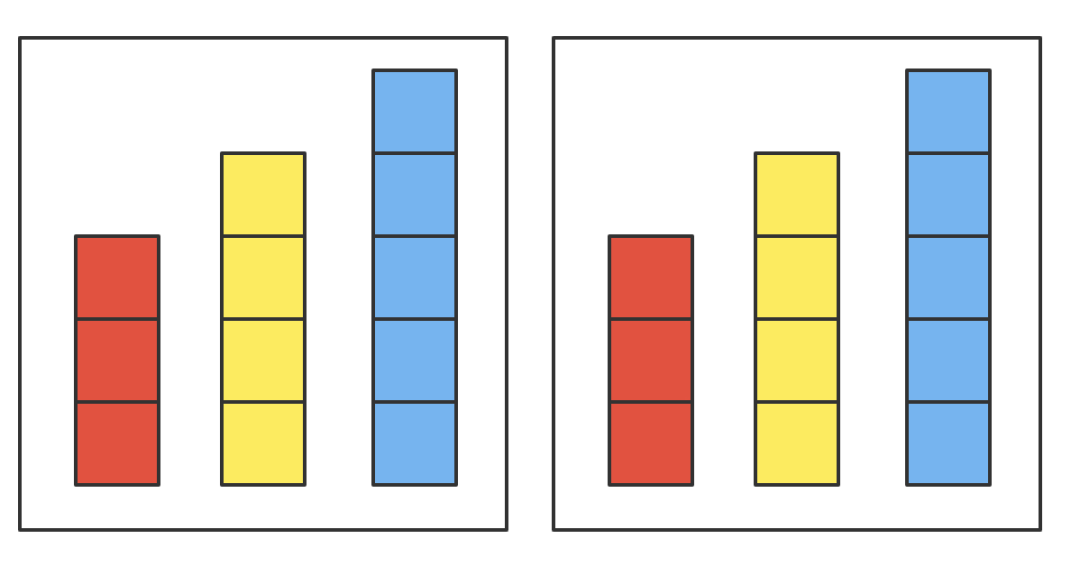
此时后手又可以进入无赖状态,不停模仿先手的动作,使得先手总是面对这种对称的局面。所以 是偶数时的对称局面,是必败的。
接着思考, 是偶数时,先手如何构造对称局面,从而让对手必败呢?
设 堆石子的数量分别为 , , ..., ,因为选手可以操作任意一堆石子,所以不妨规定 是一个单调递增序列。
为了构造对称局面,不妨操作 ,让 ,因为这样可以拿出最多的自由石子,即个石子,放入 ,使得 ,,...,。
为了满足上述操作,必须保证:
移项得:
总结一下,当 是偶数时,如果满足上述要求,则为必胜局面,反之为必败局面。
解释一下上述公式:因为是单调递增的,所以不等式左边只会大于等于右边,且只有对称局面时,两边才会相等。因此,当 是偶数时,对称局面时必败局面,非对称局面时必胜局面。
继续讨论 是奇数时,仍然令 是一个单调递增序列,只要满足:
先手就可通过操作,让后手进入对称局面。
通过对上式移项得:
因为 是一个单调递增序列,所以上式恒成立。所以 是奇数时,先手必胜。
思考过程有点麻烦,代码很简单~
#include
#include
#include
#include
using namespace std;
int main() {
int n;
int seq[10];
while(scanf("%d", &n) != EOF && n) {
for (int i = 0; i < n; i++) {
scanf("%d", seq + i);
}
if (n & 1) {
puts("1");
} else {
sort(seq, seq+n);
bool flag = true;
for (int i = 0; i < n && flag; i += 2) {
if (seq[i] != seq[i+1]) {
flag = false;
}
}
if (flag) {
puts("0");
} else {
puts("1");
}
}
}
return 0;
}
