激活还是不激活?CVPR2021-Activate Or Not
简介
在该工作中,我们提出了一种名为ACON(Activate Or Not)激活函数。此外,我们发现由NAS搜索得到的Swish函数,是我们常用的ReLU激活函数的平滑形式。我们将该形式推广到ReLU函数的其他变体(Leaky-ReLU, PReLU等)。最后我们提出了一个meta-ACON激活函数和其设计空间,它可以自适应的选择是否激活神经元,通过替换原网络的激活层,能提升1-2个点的网络精度(ResNet-152)。
论文地址:Activate or Not: Learning Customized Activation(https://arxiv.org/abs/2009.04759)
代码地址:nmaac/ACON.pytorch(https://github.com/nmaac/ACON.pytorch)
Smooth Maximum
我们常用的ReLU激活函数本质是一个MAX函数,其公式如下
而MAX函数的平滑,可微分变体我们称为Smooth Maximum,其公式如下
其中 是一个平滑因子,当 趋近于无穷大时,Smooth Maximum就变为标准的MAX函数,而当 为0时,Smooth Maximum就是一个算术平均的操作
这里我们只考虑Smooth Maximum只有两个输入量的情况,于是有以下公式
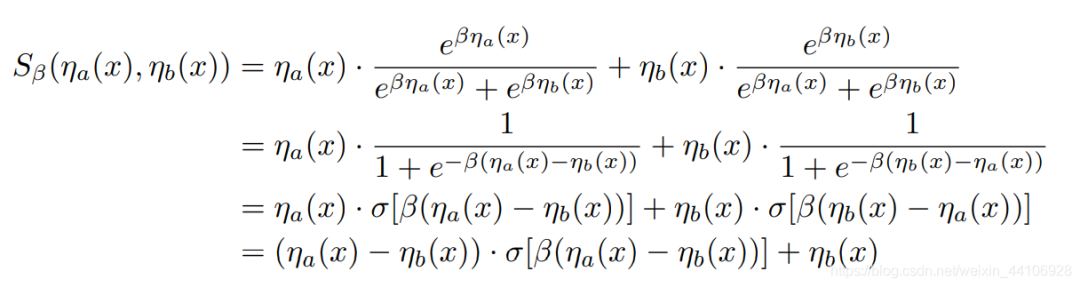
其中 表示 sigmoid函数
笔者写了一段关于Smooth Maximum的代码
import numpy as np
import matplotlib.pyplot as plt
def smooth_maximum(x, x1_func, x2_func, beta=0.0):
"""
Smooth Maximum
:param x: The input variable
:param x1_func: The functor of n1
:param x2_func: The functor of n2
:param beta: The beta value
:return:
"""
a_x = x1_func(x)
b_x = x2_func(x)
e_beta_a_x = np.exp(beta * a_x)
e_beta_b_x = np.exp(beta * b_x)
return ((a_x * e_beta_a_x) + (b_x * e_beta_b_x)) / (e_beta_a_x + e_beta_b_x)
从ReLU推广到Swish
考虑平滑形式下的ReLU,即
代入公式我们得到
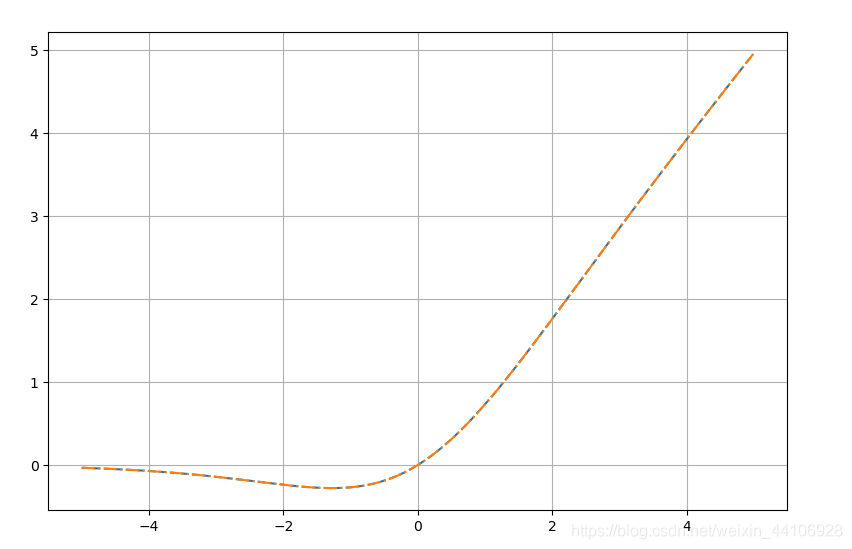
而这个结果就是Swish激活函数!所以我们可以得到,Swish激活函数是ReLU函数的一种平滑近似。我们称其为ACON-A
我们也可以用上述代码验证下
def swish(x, beta=1.0):
return beta * x / (1 + np.exp(-x))
Acon_a = lambda x: smooth_maximum(x, x1_func=lambda x: x, x2_func=lambda x: 0, beta=1.0)
x = np.arange(-5, 5, 0.01).astype(np.float32)
acon_a_out = Acon_a(x)
swish_out = swish(x)
plt.plot(x, acon_a_out, ls='--')
plt.plot(x, swish_out, ls='-.')
plt.grid()
plt.show()
ACON-B
上述的平滑形式可以推广到ReLU激活函数家族里(PReLU,Leaky-ReLU)
因此我们提出了ACON-B的变体,即
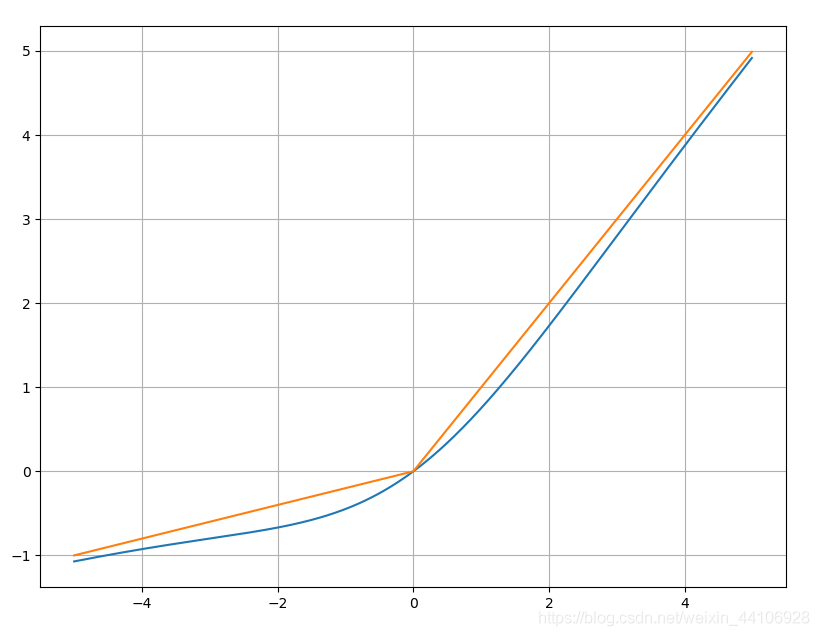
我们按照前面的代码实验一下Leaky ReLU和它的平滑形式
def leaky_relu(x, beta):
return np.maximum(x, beta * x)
Acon_b = lambda x: smooth_maximum(x, x1_func=lambda x: x, x2_func=lambda x: 0.2 * x, beta=1.0)
x = np.arange(-5, 5, 0.01).astype(np.float32)
acon_b_out = Acon_b(x)
leaky_relu_out = leaky_relu(x, 0.2)
plt.plot(x, acon_b_out)
plt.plot(x, leaky_relu_out)
plt.grid()
plt.show()
ACON-C
最后我们提出最广泛的一种形式ACON-C,即
它能涵盖之前的,甚至是更复杂的形式,在代码实现中,p1和p2使用的是两个可学习参数来自适应调整
我们简单看下ACON-C的函数性质
对其求一阶导,可以得到
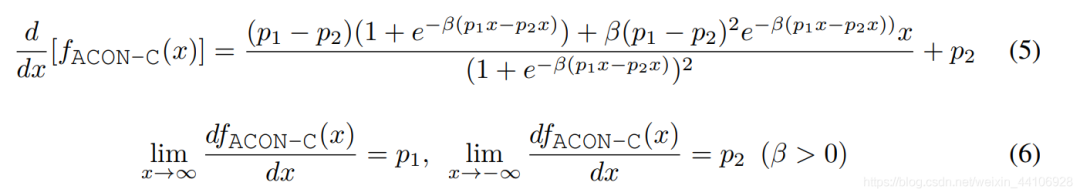
当 x 趋近于正无穷时,其梯度为 p1,当x趋近于负无穷时,其梯度为 p2。
对其求二阶导,有
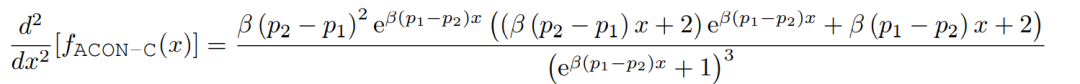
为了得到一阶导的上下界,我们令其二阶导为0,求得一阶导上下界分别为
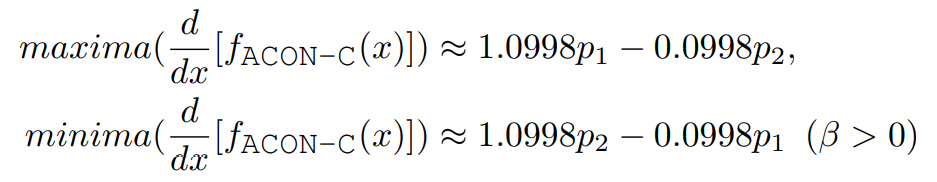
可以看到ACON-C下,一阶导的上下界也是通过p1和p2两个参数来共同决定的
最后总结下各个形态的公式

Meta-ACON
前面我们有提到,ACON系列的激活函数通过 的值来控制是否激活神经元(为0,即不激活)。因此我们需要为ACON设计一个计算 的自适应函数。
而自适应函数的设计空间包含了layer-wise,channel-wise,pixel-wise这三种空间,分别对应的是层,通道,像素。
这里我们选择了channel-wise,首先分别对H, W维度求均值,然后通过两个卷积层,使得每一个通道所有像素共享一个权重。公式如下
为了节省参数量,我们在和之间加了个缩放参数r,我们设置为16
代码解读
具体的代码很简单,实现为:
import torch
from torch import nn
class MetaAconC(nn.Module):
r""" ACON activation (activate or not).
MetaAconC: (p1*x-p2*x) * sigmoid(beta*(p1*x-p2*x)) + p2*x
"""
def __init__(self, width):
super().__init__()
self.fc1 = nn.Conv2d(width, width//16, kernel_size=1, stride=1, bias=False)
self.fc2 = nn.Conv2d(width//16, width, kernel_size=1, stride=1, bias=False)
self.p1 = nn.Parameter(torch.randn(1, width, 1, 1))
self.p2 = nn.Parameter(torch.randn(1, width, 1, 1))
self.sigmoid = nn.Sigmoid()
def forward(self, x, **kwargs):
beta = self.sigmoid(self.fc2(self.fc1(x.mean(dim=2, keepdims=True).mean(dim=3, keepdims=True))))
return (self.p1 * x - self.p2 * x) * self.sigmoid( beta * (self.p1 * x - self.p2 * x)) + self.p2 * x
首先作者设置了p1和p2这两个可学习参数,并且设置了fc1和fc2两个1x1卷积。在前向过程中,首先计算beta,x首先在H和W维度上求均值,然后经过两层1x1卷积,最后由sigmoid激活函数得到一个(0, 1)的值,用于控制是否激活。
接着就是按照前面的公式进行计算,大家可以参考上文的图
实验
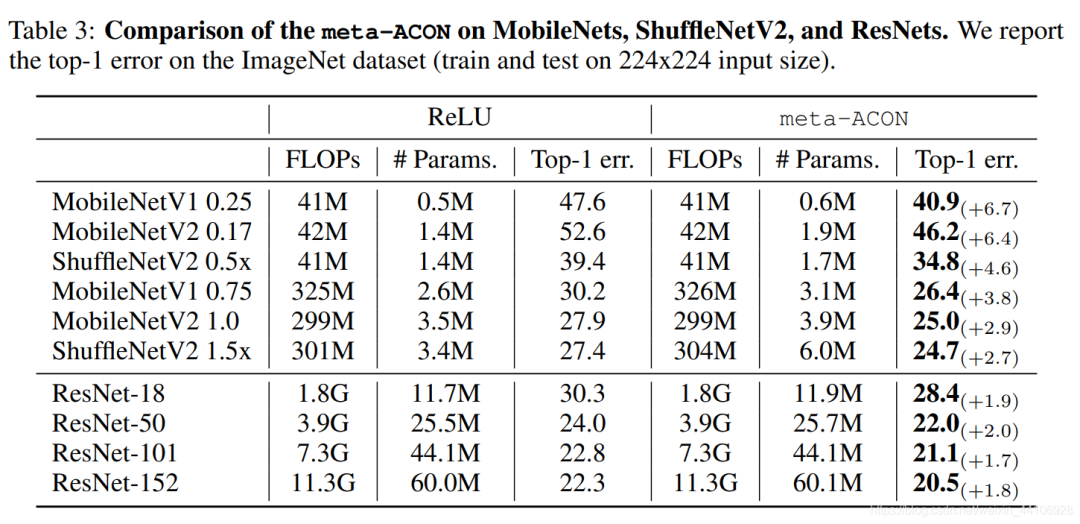
作者针对不同大小的网络做出了调整,针对小网络它替换了所有ReLU激活层,针对大网络(如ResNet50/101)只替换了每一个Block中3x3卷积后面的ReLU激活层,作者怎么设置的理由是避免过拟合,但我个人认为如果全都换成Meta-ACON,额外增加的参数量是很大的。
Meta-ACON虽然带来了一定的参数量,但是对大网络和小网络上都是有一定的提升
作者还针对设计空间做了一系列消融实验,其中channel-wise的效果是最好的
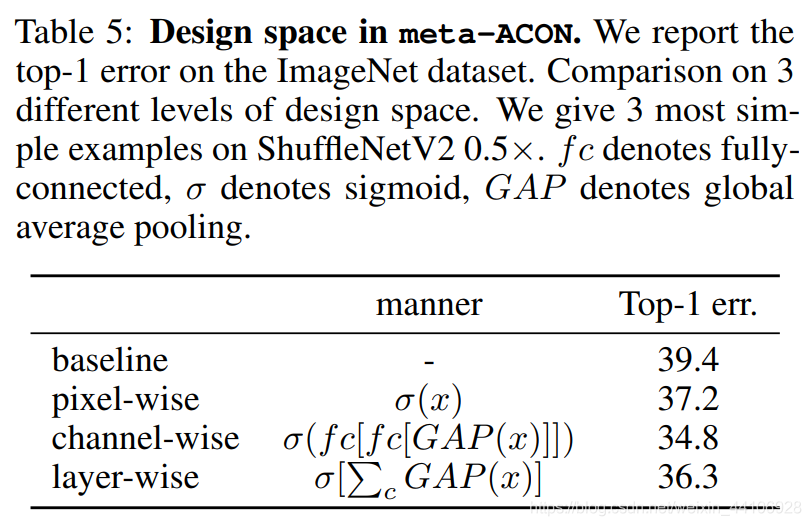
小结
该工作是之前旷视FReLU激活函数,ShuffleNet的作者MaNingNing提出的,构思十分巧妙,将ReLU和NAS搜索出来的Swish激活函数联系起来,并推广到一般的形式,为了让网络自适应的调整是否激活,设置了两层1x1卷积来控制。从实验上也从各个角度论证其有效性,期待后续对激活函数的进一步探索。
欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享,坚持原创,每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧
有对文章相关的问题,或者想要加入交流群,欢迎添加BBuf微信:
为了方便读者获取资料以及我们公众号的作者发布一些Github工程的更新,我们成立了一个QQ群,二维码如下,感兴趣可以加入。
