ZOJ 1017 The Bermuda Triagle
The Bermuda Triagle
People in the hidden region of the Bermuda Triangle make everything they need in triangular shapes. One day, someone decided to break the rule and bake a hexagonally shaped cake. But as usual, he has to serve the cake in triangular pieces. The pieces are equilateral triangles but in different sizes for different people. He can use as many triangles as needed to cut the cake into pieces, such that nothing remains from the cake. For example, the following figure shows one way that a hexagon with side 9 can be cut into triangles with side 2 and 3. (The cake is cut along the thick lines, thin lines are drawn to show the sizes).
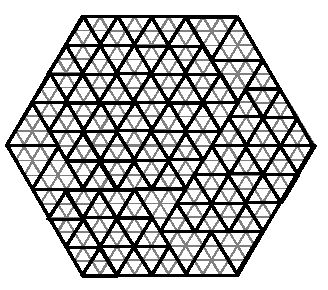
Input is a hexagon and triangle types (specified by the length of their sides) and the goal is to decide if the hexagon can be completely divided by the given triangle types.
Input
The first line of the input contains a single integer t (1 <= t <= 10), the number of test cases, followed by the input data for each test case. Each test case consists of a single line, containing s (1 <= s <= 25), the length of the hexagon's side, followed by n, the number of triangle types (1 <= n <= 10), followed by n integers representing the length of each triangle type's side (between 1 and 25, inclusive).
Output
There should be one output line per test case containing either YES or NO depending on whether the hexagon can be completely divided by the given triangle types.
Sample Input
3
5 2 2 3
7 2 3 2
13 2 2 3
Sample Output
NO
NO
YES
百慕大三角
百慕大三角隐秘区域的人们把他们需要的一切都做成三角形。有一天,有人决定打破这个规矩,烤了一个六边形的蛋糕。但像往常一样,他必须把蛋糕做成三角形。这些小块是等边三角形,但不同的人有不同的尺寸。他可以根据需要使用多少三角形来把蛋糕切成块,这样蛋糕就不会剩下任何东西。例如,下图展示了一个边为9的六边形可以被切成边为2和3的三角形的一种方法。(蛋糕按粗线切,用细线表示大小)。
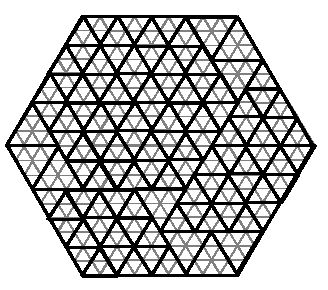
输入是一个六边形和三角形类型(由它们的边长指定),目标是确定六边形是否可以被给定的三角形类型完全分割。
输入
输入的第一行包含一个单一的整数t (1 <= t <= 10),测试用例的数量,然后是每个测试用例的输入数据。每个测试用例包括一行,包含(1 < =年代< = 25),六边形的边的长度,紧随其后的是n,三角形的类型(1 < = n < = 10),其次是n个整数代表每个三角形类型的边的长度(1 - 25、包容)。
输出
每个测试用例应该有一个输出行,包含YES或NO,这取决于六边形是否可以被给定的三角形类型完全分割。
Sample Input
3
5 2 2 3
7 2 3 2
13 2 2 3
Sample Output
NO
NO
YES

代码:
# include <stdio.h>
# include <stdlib.h>
# include <stdbool.h>
bool map[52][52];
int num,n,list[11];
void printmap()
{
int i,j;
for(i=1;i<=2*n;i++)
{
for(j=1;j<4*n;j++) printf("%d ",map[i][j]);
printf("\n");
}
printf("\n\n");
}
bool canput(int r,int c,int len)
{
int i,j;
if(r+len-1>2*n||c+len-1>4*n) return 0;
if(c%2==0)
{
for(i=r;i<r+len;i++)
for(j=c+2*(i-r);j<c+2*(i-r)+2*len-1-2*(i-r);j++)
if(map[i][j]) return 0;
}
else
{
for(i=r;i<r+len;i++)
for(j=c;j<c+2*(i-r+1)-1;j++)
if(map[i][j]) return 0;
}
return 1;
}
void put(int r,int c,int len)
{
int i,j;
if(c%2==0)
{
for(i=r;i<r+len;i++)
for(j=c+2*(i-r);j<c+2*(i-r)+2*len-1-2*(i-r);j++)
map[i][j]=1;
}
else
{
for(i=r;i<r+len;i++)
for(j=c;j<c+2*(i-r+1)-1;j++)
map[i][j]=1;
}
}
void deput(int r,int c,int len)
{
int i,j;
if(c%2==0)
{
for(i=r;i<r+len;i++)
for(j=c+2*(i-r);j<c+2*(i-r)+2*len-1-2*(i-r);j++)
map[i][j]=0;
}
else
{
for(i=r;i<r+len;i++)
for(j=c;j<c+2*(i-r+1)-1;j++)
map[i][j]=0;
}
}
bool detect(int r,int c)
{
if(r>2*n) return 1;
else if(c>4*n) return detect(r+1,1);
else if(map[r][c])
{
int i;
for(i=c;i<=4*n;i++)
if(!map[r][i]) break;
return detect(r,i);
}
else
{
int i;
for(i=1;i<=num;i++)
{
if(canput(r,c,list[i]))
{
put(r,c,list[i]);
if(detect(r,c+1)) return 1;
deput(r,c,list[i]);
}
else break;
}
return 0;
}
}
int cmp(const void *a,const void *b)
{
return *(int *)a-*(int *)b;
}
int main()
{
int test,i,k;
scanf("%d",&test);
for(i=1;i<=test;i++)
{
int j;
bool flag=0;
scanf("%d",&n);
scanf("%d",&num);
for(j=1;j<=num;j++) scanf("%d",&list[j]);
qsort(list+1,num,sizeof(int),cmp);
for(j=1;j<=num;j++)/*优化*/
{
if(n%list[j]==0)
{
printf("YES\n");
flag=1;
break;
}
if(list[j]>n)
{
num=j-1;
break;
}
}
if(flag) continue;
for(j=1;j<=num;j++)
for(k=1;k<j;k++)
{
if(list[j]%list[k]==0)
{
int l;
for(l=j;l<num;l++) list[l]=list[l+1];
j--;
num--;
break;
}
}
/*---------------------------------------------*/
memset(map,1,sizeof(map));
for(j=1;j<=n;j++)
for(k=1;k<=2*n+1+(j-1)*2;k++)
map[j][k]=0;
for(j=n+1;j<=2*n;j++)
for(k=(j-n)*2;k<=4*n;k++)
map[j][k]=0;
if(detect(1,1)) printf("YES\n");
else printf("NO\n");
}
return 0;
}
