我们应该搞清楚分支预测
分支预测的英文名字是「Branch Prediction」
大家可以在Google上搜索这个关键字,可以看到关于分支预测的很多内容,不过要搞清楚分支预测如何工作的,才是问题的关键。

分支预测对程序的影响
我们来看看下面的两段代码
代码1
#include
#include
#include
int main()
{
// Generate data
const unsigned arraySize = 32768;
int data[arraySize];
for (unsigned c = 0; c < arraySize; ++c)
data[c] = std::rand() % 256;
// !!! With this, the next loop runs faster.
//std::sort(data, data + arraySize);
// Test
clock_t start = clock();
long long sum = 0;
for (unsigned i = 0; i < 100000; ++i) {
for (unsigned c = 0; c < arraySize; ++c) { // Primary loop
if (data[c] >= 128) sum += data[c];
}
}
double elapsedTime = static_cast<double>(clock()-start) / CLOCKS_PER_SEC;
std::cout << elapsedTime << '\n';
std::cout << "sum = " << sum << '\n';
}执行结果
@ubuntu:/data/study$ g++ fenzhi.cpp && ./a.out
21.6046
sum = 314931600000代码2
#include
#include
#include
int main()
{
// Generate data
const unsigned arraySize = 32768;
int data[arraySize];
for (unsigned c = 0; c < arraySize; ++c)
data[c] = std::rand() % 256;
// !!! With this, the next loop runs faster.
std::sort(data, data + arraySize);
// Test
clock_t start = clock();
long long sum = 0;
for (unsigned i = 0; i < 100000; ++i) {
for (unsigned c = 0; c < arraySize; ++c) { // Primary loop
if (data[c] >= 128) sum += data[c];
}
}
double elapsedTime = static_cast<double>(clock()-start) / CLOCKS_PER_SEC;
std::cout << elapsedTime << '\n';
std::cout << "sum = " << sum << '\n';
}执行结果:
@ubuntu:/data/study$ g++ fenzhi.cpp && ./a.out
8.52157
sum = 314931600000第一段代码生成随机数组后,没有进行排序,第二段代码对随机的数组进行排序,执行的时间上发生了非常大的差异。

所以,他们发生了什么事情呢?
导致他们结果不同的原因,就是分支预测,分支预测是CPU处理器对程序的一种预测,和CPU架构有关系,现在的很多处理器都有分支预测的功能。
CPU在执行这段代码的时候
if (data[c] >= 128) sum += data[c];CPU会有一个提前预测机制,比如前面的执行结果都是true,那么下一次在判断if的时候,就会默认认为是true来处理,让下面的几条指令提前进入预装。
当然,这个判断不会影响实际的结果输出,这个判断只是为了让CPU并行执行代码。
CPU执行一条指令分为几个阶段

既然是分阶段执行,也就是我们正常说的pipeline(流水线执行)。
流水线的工人只要完成自己负责的内容就好了,没有必要去关心其他的人处理。
那如果我有一段代码,如下:
int a = 0;
a += 1;
a += 2;
a += 3;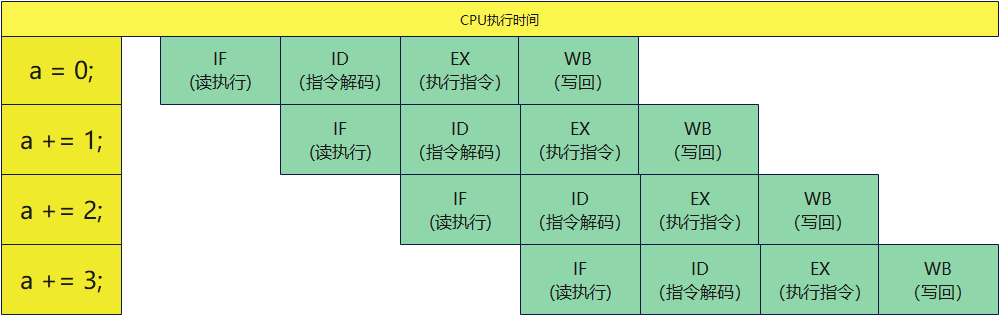
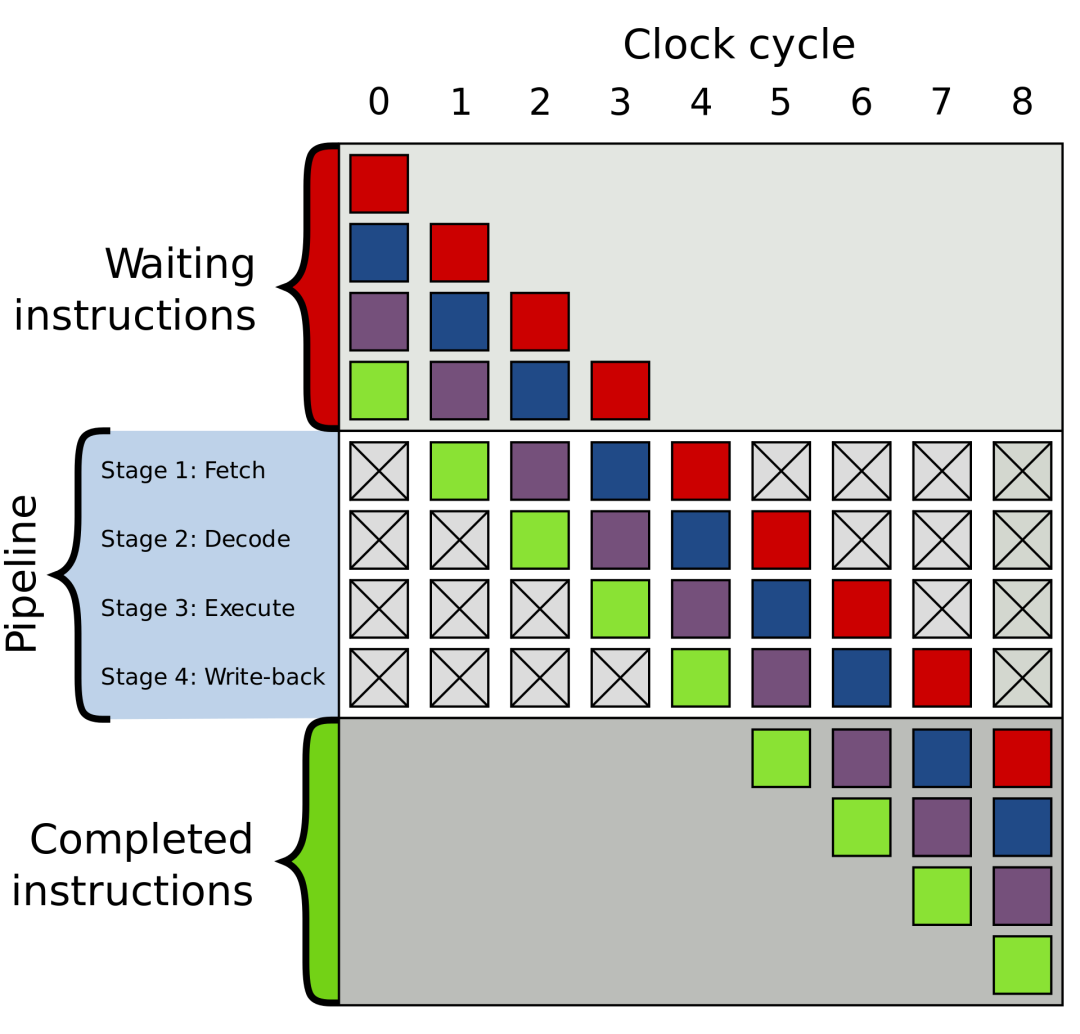
从这个图上我们可以看到,我们认为是在执行 a = 0结束后,才会执行a+=1。
但是实际CPU是在执行a=0的第一条执行后,马上就去执行a+=1的第一条指令了。
也就因为这样,执行速度上得到了大幅度的提升。
但是对于if() 语言,在没有分支预测的时候,我们需要等待if()执行出现结果后才能继续执行下一个代码。

如果存在分支预测的情况

通过比较我们可以发现,如果存在分支预测的时候,就让执行速度变快了。

那如果预测失败,会不会就影响了执行的时间,答案是肯定的。
在前面的例子中,没有对数组排序的情况下,分支预测大部分都会是失败的,这个时候就会在执行结束后重新取指令执行,会严重影响执行效率。
而在排序后的例子中,分支预测一直处于成功的状态,CPU的执行速率得到大幅度的提升。

如果解决分支预测引起的性能下降
分支预测一定会存在一定的能性下降,想让性能提升的方法就是不要使用这个该死的if语句。
比如,上面的代码,我们可以修改成这样
#include
#include
#include
int main()
{
// Generate data
const unsigned arraySize = 32768;
int data[arraySize];
for (unsigned c = 0; c < arraySize; ++c)
data[c] = std::rand() % 256;
// !!! With this, the next loop runs faster.
//std::sort(data, data + arraySize);
// Test
clock_t start = clock();
long long sum = 0;
for (unsigned i = 0; i < 100000; ++i) {
for (unsigned c = 0; c < arraySize; ++c) { // Primary loop
int t = (data[c] - 128) >> 31;
sum += ~t & data[c];
}
}
double elapsedTime = static_cast<double>(clock()-start) / CLOCKS_PER_SEC;
std::cout << elapsedTime << '\n';
std::cout << "sum = " << sum << '\n';
}比如,我们看到的绝对值代码,里面也用了这样的思想
/**
* abs - return absolute value of an argument
* @x: the value. If it is unsigned type, it is converted to signed type first.
* char is treated as if it was signed (regardless of whether it really is)
* but the macro's return type is preserved as char.
*
* Return: an absolute value of x.
*/
#define abs(x) __abs_choose_expr(x, long long, \
__abs_choose_expr(x, long, \
__abs_choose_expr(x, int, \
__abs_choose_expr(x, short, \
__abs_choose_expr(x, char, \
__builtin_choose_expr( \
__builtin_types_compatible_p(typeof(x), char), \
(char)({ signed char __x = (x); __x<0?-__x:__x; }), \
((void)0)))))))
#define __abs_choose_expr(x, type, other) __builtin_choose_expr( \
__builtin_types_compatible_p(typeof(x), signed type) || \
__builtin_types_compatible_p(typeof(x), unsigned type), \
({ signed type __x = (x); __x < 0 ? -__x : __x; }), other)当然,你也可以这样写
int abs(int i){
if(i<0)
return ~(--i);
return i;
}所以说,计算机的尽头是数学
参考:
https://stackoverflow.com/questions/11227809/why-is-processing-a-sorted-array-faster-than-processing-an-unsorted-array/11227902#11227902
https://blog.csdn.net/loongshawn/article/details/118339009
https://blog.csdn.net/DBC_121/article/details/105360658
