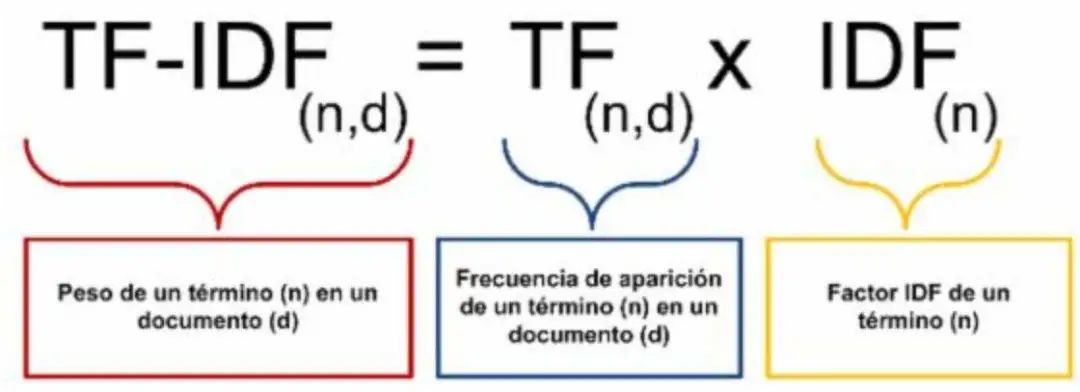
万万没想到,TF-IDF是这么计算的!
一、了解tf-idf
对于文本处理,tf-idf的使用已经非常普遍,在sklearn等知名的机器学习开源库中都提供了直接的调用,然而很多人并没有搞清楚TF-IDF是怎么算出来的,也就无法对这种计算方法进行针对性的改进了。我之前也是稀里糊涂的,在各种开源库随手可得的Python年代“调包需谨慎”,不能让自己成为只会调包的人,我们内功还是需要修炼的,计算之前,我们先了解下tf-idf的基本定义。
tf(term frequency:指的是某一个给定的词语在该文件中出现的次数,这个数字通常会被归一化(一般是词频除以该文件总词数),以防止它偏向长的文件。
idf (inverse document frequency):反应了一个词在所有文本(整个文档)中出现的频率,如果一个词在很多的文本中出现,那么它的idf值应该低,而反过来如果一个词在比较少的文本中出现,那么它的idf值应该高。
一个词语的重要性随着它在文件中出现的次数成正比增加,但同时会随着它在语料库中出现的频率成反比下降。
下面我们看看大多数情况下,tf-idf 的定义:
TF的计算公式如下:
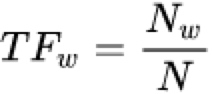
其中![]() 是在某一文本中词条w出现的次数,
是在某一文本中词条w出现的次数,![]() 是该文本总词条数。
是该文本总词条数。
IDF的计算公式:
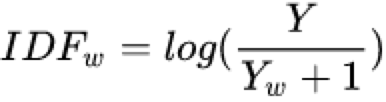
其中Y是语料库的文档总数,Yw是包含词条w的文档数,分母加一是为了避免![]() 未出现在任何文档中从而导致分母为
未出现在任何文档中从而导致分母为![]() 的情况。
的情况。
TF-IDF的就是将TF和IDF相乘
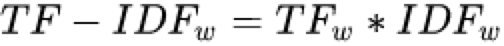
从以上计算公式便可以看出,某一特定文件内的高词语频率,以及该词语在整个文件集合中的低文件频率,可以产生出高权重的TF-IDF。因此,TF-IDF倾向于过滤掉常见的词语,保留重要的词语。
二、手算tf-idf
现在我们来看看,tf-idf到底怎么计算的,和我们手算的能不能对上。
在sklearn中,tf与上述定义一致,我们看看idf在sklearn中的定义,可以看到,分子分母都加了1,做了更多的平滑处理
smooth_idf=False
idf(t) = log [ n / df(t) ] + 1
smooth_idf=True
idf(t) = log [ (1 + n) / (1 + df(t)) ] + 1
下面我们手把手的计算出TF-IDF的值,使用的是sklearn官方的案例:
corpus = ['This is the first document.','This document is the second document.','And this is the third one.','Is this the first document?']#初始化vector = TfidfVectorizer()#tf-idf计算tfidf = vector.fit_transform(corpus)#直接打印,得到的是一个稀疏矩阵,第1位表示文档编号,第二位代表词的编号print(tfidf)(0, 1) 0.46979138557992045(0, 2) 0.5802858236844359(0, 6) 0.38408524091481483(0, 3) 0.38408524091481483(0, 8) 0.38408524091481483(1, 5) 0.5386476208856763(1, 1) 0.6876235979836938(1, 6) 0.281088674033753(1, 3) 0.281088674033753(1, 8) 0.281088674033753(2, 4) 0.511848512707169(2, 7) 0.511848512707169(2, 0) 0.511848512707169(2, 6) 0.267103787642168(2, 3) 0.267103787642168(2, 8) 0.267103787642168(3, 1) 0.46979138557992045(3, 2) 0.5802858236844359(3, 6) 0.38408524091481483(3, 3) 0.38408524091481483(3, 8) 0.38408524091481483
通过vocabulary_属性,可以查看每个词对应的数字编号,就可以与上面的矩阵对应起来了
vector.vocabulary_{'this': 8, 'is': 3, 'the': 6, 'first': 2, 'document': 1,'second': 5, 'and': 0, 'third': 7, 'one': 4}
通过上面的字典和矩阵可以知道,第一个文档'This is the first document'的tf-idf 值如下
(0, 1) 0.46979138557992045 document(0, 2) 0.58028582368443590 first(0, 6) 0.38408524091481483 the(0, 3) 0.38408524091481483 is(0, 8) 0.38408524091481483 this
document first the is this
0.46979 0.58028 0.384085 0.38408 0.384085
我们手动计算来验证下:
tf 计算
对于第一个文档,有5个不同的词,每个词的词频为:tf= 1/5
idf计算
document:log((1+N)/(1+N(document)))+1= log((1+4)/(1+3))+1 = 1.2231435first :log((1+N)/(1+N(first)))+1 = log((1+4)/(1+2))+1 = 1.5108256the :log((1+N)/(1+N(the )))+1 = log((1+4)/(1+4))+1 = 1.0is :log((1+N)/(1+N(is )))+1 = log((1+4)/(1+4))+1 = 1.0this :log((1+N)/(1+N(this)))+1 = log((1+4)/(1+4))+1 = 1.0

tf-idf计算
1.2231435*1/5 = 0.244628691.5108256*1/5 = 0.302165121.0*1/5 = 0.21.0*1/5 = 0.21.0*1/5 = 0.2
得到我们手工计算的tf-idf值

和我们sklearn计算的
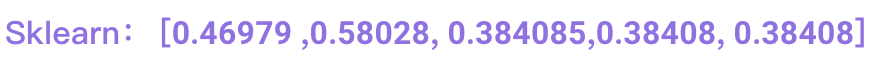
答案并不对,哪里出了问题呢?我们仔细看看原来的代码,因为sklearn做了归一化,我们按同样的方法进行归一化计算如下:
计算每个tf-idf 的平方根
(0.24462869**2 + 0.30216512**2 + 0.2**2 + 0.2**2 + 0.2**2)**0.5= 0.5207177313
对每个值除以平方根
0.24462869/0.5207177313244965 = 0.46979135774340350.30216512/0.5207177313244965 = 0.58028582823829230.20000000/0.5207177313244965 = 0.38408524997080550.20000000/0.5207177313244965 = 0.38408524997080550.20000000/0.5207177313244965 = 0.3840852499708055
这样一看,就和我们的sklearn计算的一致了,到此,我们也算是学会了计算tf-idf值了,加深了对该方法的理解,以便于后期的算法调用,心里有货,才不惧未知。