用香蕉驱动一个随机数生成器,靠谱吗?

来源:大数据文摘 本文约3500字,建议阅读7分钟
香蕉的用途又增加了!

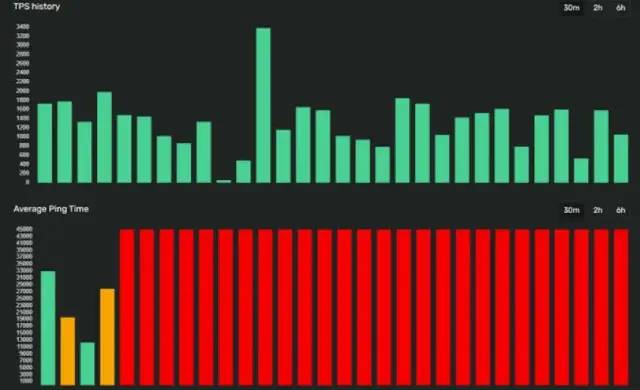
每个数字出现在列表中的概率必须与其他每个数字相同(取一个参考区间),也即均匀分布。 数字的序列必须是事先无法预测的。


#include <stdio.h>#include <assert.h>#include <stdlib.h>#include <stdint.h>int main(int argc, char const *argv[]) {FILE * lettura = fopen("textsample.txt", "r");assert(lettura != NULL);FILE * scrittura = fopen("sample.txt", "wb");assert(scrittura != NULL);uint16_t N = 0; //N is 16 byteschar bytes[2];char buffer[6]; // 5 char + terminatordo{fscanf(lettura,"%s",buffer); // put one line in the bufferN = atoi(buffer); // from char array to integerbytes[0] = (N >> 8); // take the 8 msbbytes[1] = (N & 0xFF); // take the 8 lsbfwrite(bytes, 1, sizeof(bytes), scrittura); // output raw msb and lsb}while (!feof(lettura));fclose(lettura);fclose(scrittura);return 0;}
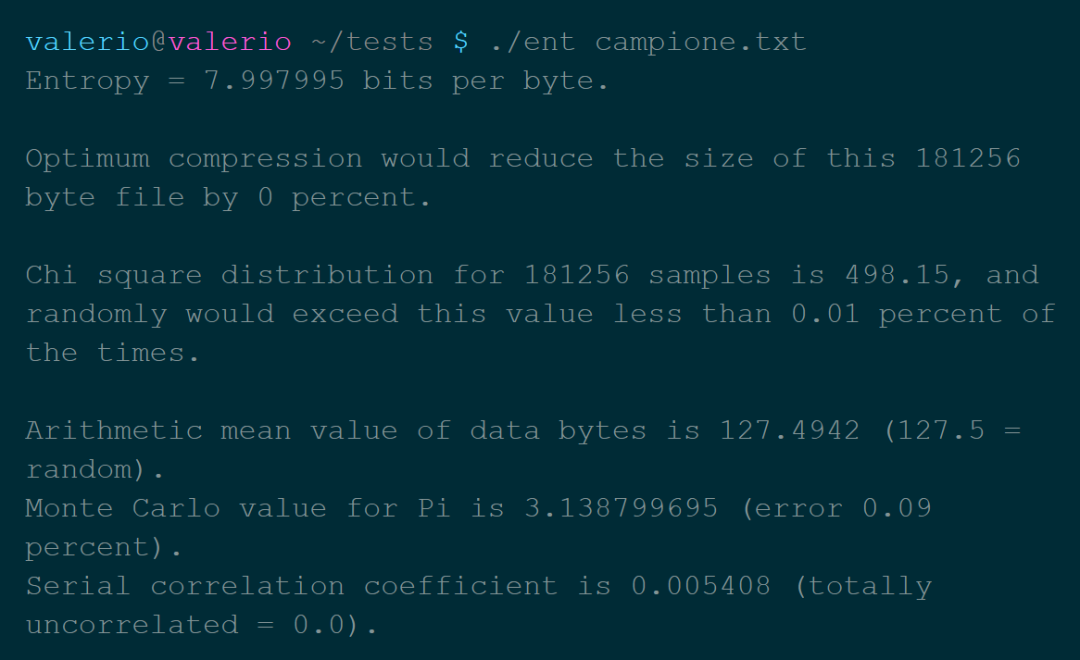
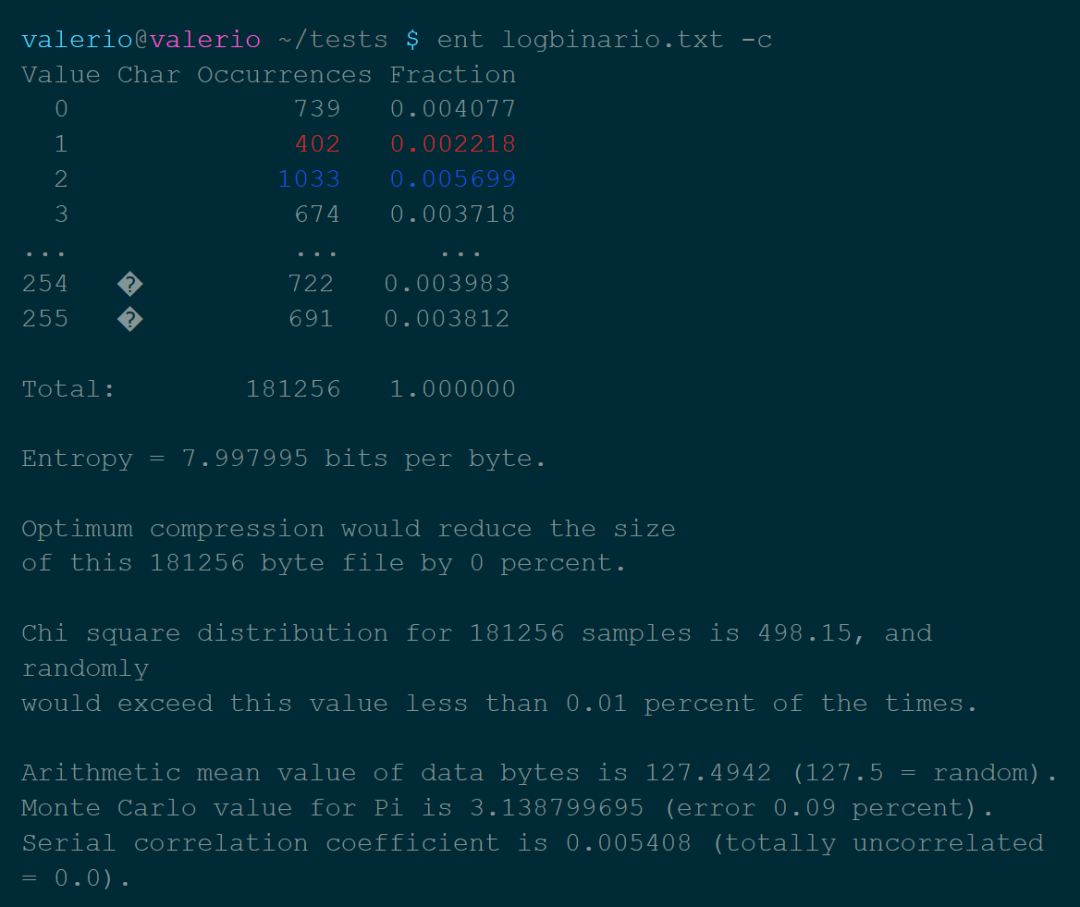
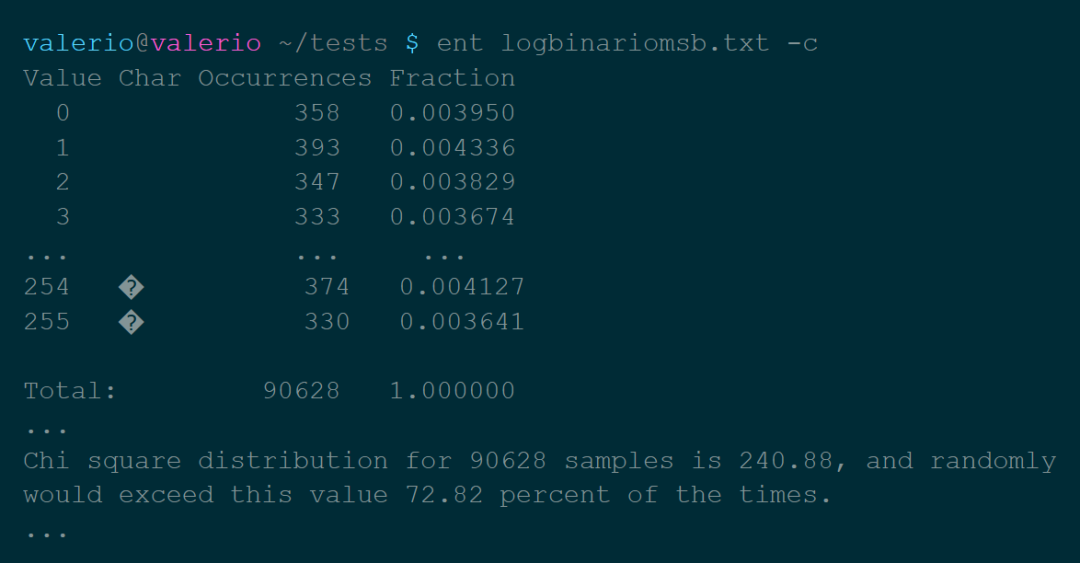
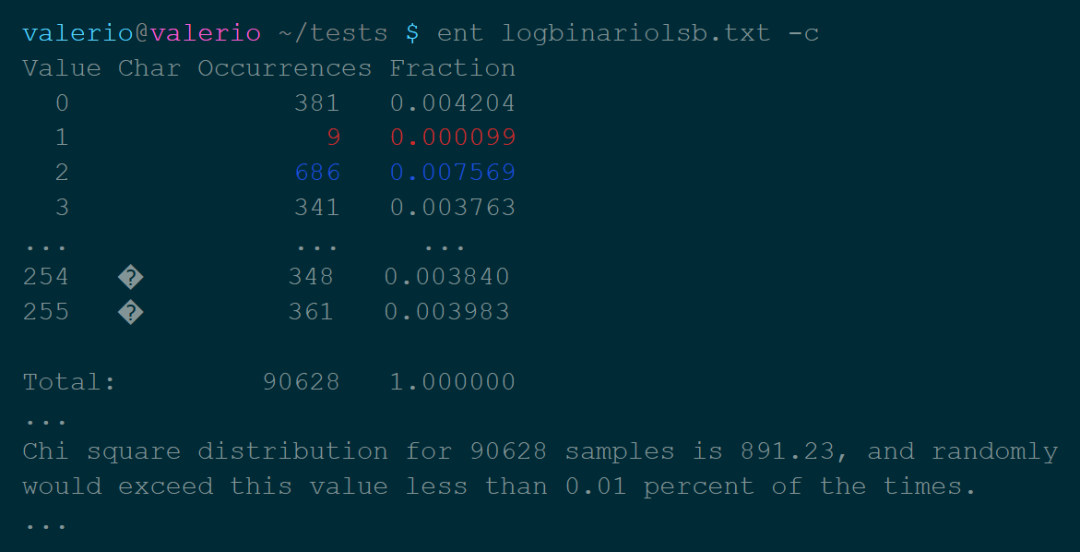
熵:熵是一部分信息中包含的“随机性”的数量。信息理论告诉我们,理论上可以通过压缩而不损失信息的最小尺寸,由熵值表示。 卡方分布:这个测试是用来了解我们的数值分布对理论分布的遵守程度。从ent手册来看,这个值应该尽可能地接近256,百分比值在10-90%之间。 算术平均值:比特的简单算术平均值。由于数值在0到255之间,所以它应该大约等于127。 用蒙特卡洛方法计算π的值:在这里更多的是一个漂亮的数据,而不是一个有用的方法。 自相关:表示系列值之间的依赖性,在最佳情况下必须等于零。
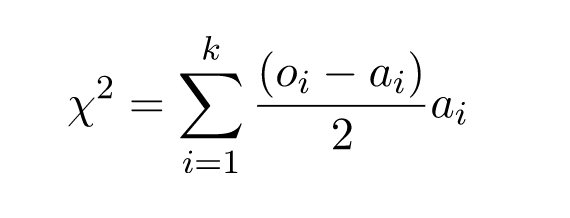
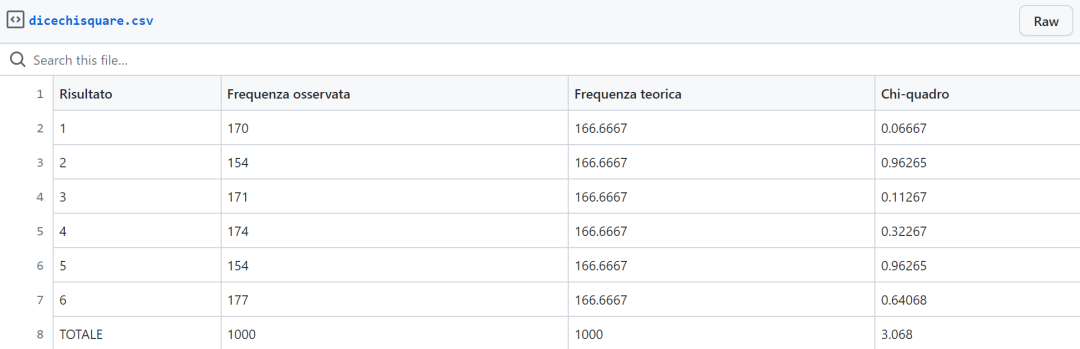
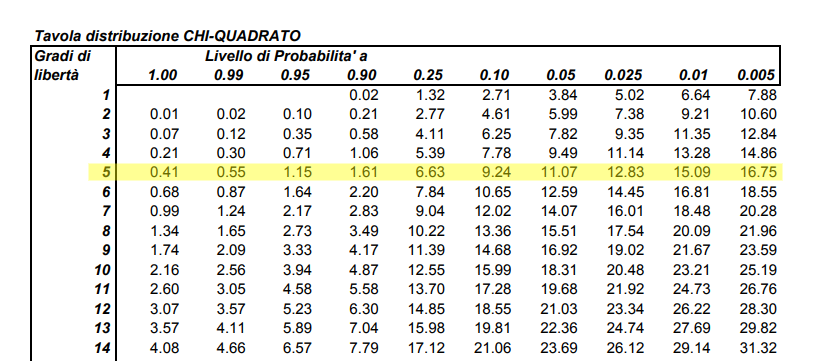
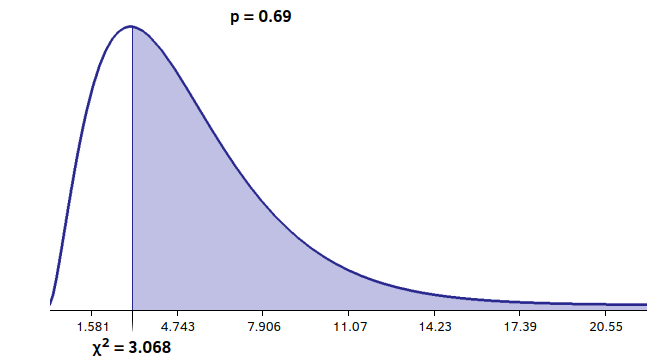
表中的行代表系统的自由度,在模具案例中,有5个自由度。列代表计算值大于表格中的值的概率水平。也有一些表格表示计算值小于的概率,这些表格被称为左尾表,上面显示的表格是右尾表。这是因为在一种情况下考虑的是图形的右边,而在另一种情况下考虑的是左边。案例中chi^2=3.068,这介于90%和25%的情况之间。这足以说明,从我们可以归类为随机的行为来看,没有过度的变化。


https://www.valerionappi.it/brng-en/
编辑:于腾凯
校对:林亦霖
评论
