引言

本着“凡我不能创造的，我就不能理解”的思想，本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架，该框架类似PyTorch能实现自动求导。

要深入理解深度学习，从零开始创建的经验非常重要，从自己可以理解的角度出发，尽量不适用外部完备的框架前提下，实现我们想要的模型。本系列文章的宗旨就是通过这样的过程，让大家切实掌握深度学习底层实现，而不是仅做一个调包侠。

逻辑回归只能处理二分类问题，但是很多时候我们遇到的是多分类问题。此时就需要用到多元逻辑回归(multinomial logistic regression)，也称为softmax回归。本文就来了解下softmax回归。

多元逻辑回归

在softmax回归中，我们希望为每个样本从个类别中标记一个类别，假设只有一个类别是正确的。

我们使用下面的表示：每个输入对应的输出是一个长度为的向量。如果类是正确的类别，我们设，然后设置向量中所有其他元素为。即同时，这种叫作独热向量(ont-hot vector)。分类器需要输出一个估计向量。对于每个类，的值就是分类器对于概率的估计。

Softmax回归中使用Sigmoid函数的推广版——Softmax函数，来计算。

输入一个向量，其中元素可以是任意值，映射它为一个概率分布，即每个元素的值被映射到之间，同时所有映射值总和为。

对于维度为的向量，softmax定义为：

输入向量经过softmax后得到向量：

该向量内所有元素总和为，分母用于将所有的值标准化成概率。

应用Softmax

类似逻辑回归，输入是一个权重向量和一个输入向量之间的点积，加上偏差。但不同的是，这里我们要为每个类提供独立的权重向量和偏差。这样，我们的每个输出类的概率可以计算为：

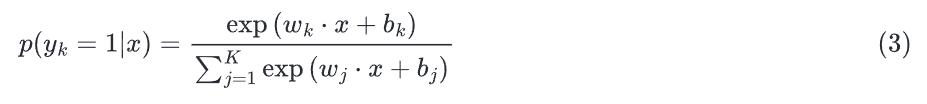
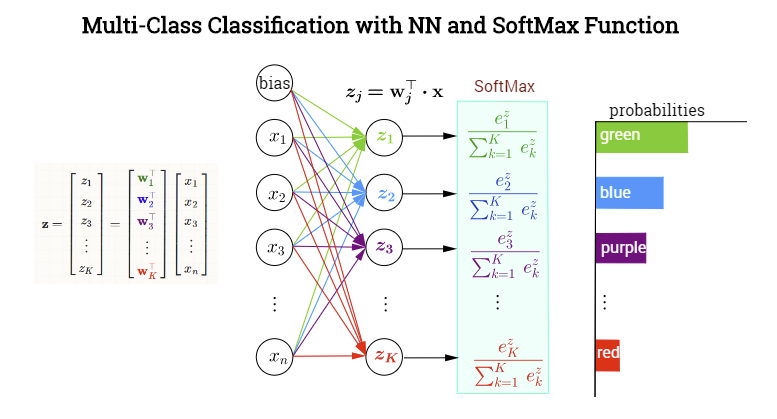
上图是公式的可视化，Softmax有个权重和偏差(上图没有体现出来)。

公式形式看起来似乎会分别计算每个输出。相反，更常见的做法是通过向量化利用GPU来更有效地计算。我们将通过将个权向量的集合表示为权矩阵和偏差向量。的第行对应于的权重向量。因此，有形状，是输出类的数量，是输入特征的数量。偏差向量对每个输出类都有一个值。如果我们用这种方式表示权值，我们可以通过一个优雅的方程来计算，一次计算个类的输出概率：

多元逻辑回归的损失函数

多元逻辑回归的损失函数是将逻辑回归的损失函数从类推广到类。回顾一下，逻辑回归的交叉熵是：

多元逻辑回归的损失函数推广了上式中的这两项(当时的和时的)。对于多元逻辑回归，和会被表示成向量。真实标签是一个带有个元素的向量，每个元素都对应一个类，假设正确的类是，则，的所有其他元素都是。模型也将生成一个带有个元素的估计向量，其中每个元素代表估计概率。

对于单个样本的损失函数，从逻辑回归推广，是个输出的对数和，每个乘上对应的，见下。这正好变成了正确类别的负对数概率：

从到是怎么转换的呢？因为只有一个类，假设记为，是正确类别，向量只有其对应的元素为，比如同时。这意味着中的求和项都是，除了正确类对应的那项。就变成了。因此交叉熵损失简单的变成了正确类别的输出概率的对数，因此称为负对数似然损失。

多元逻辑回归的梯度

当然，对于梯度下降，我们不需要损失，我们需要它的梯度。单个样本的梯度与我们在前文中看到的逻辑回归的梯度非常相似。让我们考虑一下梯度的一部分，即单个权重的导数。对于每个类，输入的第个元素的权重是，假设共有个特征。与有关的损失的偏导数是多少？因为被占用了，因此我们用新的符号。

由于分母中包含，因此我们推导如下：

其中去掉偏导符号的等式拿出来展开，第一项：

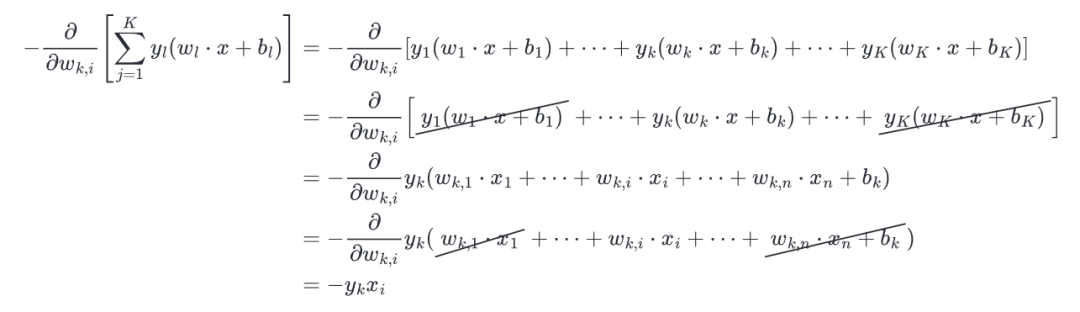
因为只有项与有关，其他的偏导数都是，所以上面进行了简化。

同理，第二项：

到是因为 与无关，因此可以提到求和符号左边。而，因此变成了。

联立公式就得到了最后的公式。

事实证明，这个导数只是类的真实值（即1或0）和类分类器输出的概率之间的差额。

多元逻辑回归与逻辑回归的关系

逻辑回归处理二分类问题，而多元逻辑回归可以处理多分类问题。那么它们之间有什么关系呢？

多元逻辑回归具有参数冗余的特点，即参数中有些是没有用的，比如从参数向量()中减去某个向量，为了方便描述，我们将偏置项增广到中，变成：

可以看到，从参数向量中减去对预测结果没有任何影响，即在模型中存在多组最优解。

假设一个样本只属于一个类别，使用多元逻辑回归来进行分类：

当类别数为2时，

利用参数冗余的特点，我们将参数减去，变成了

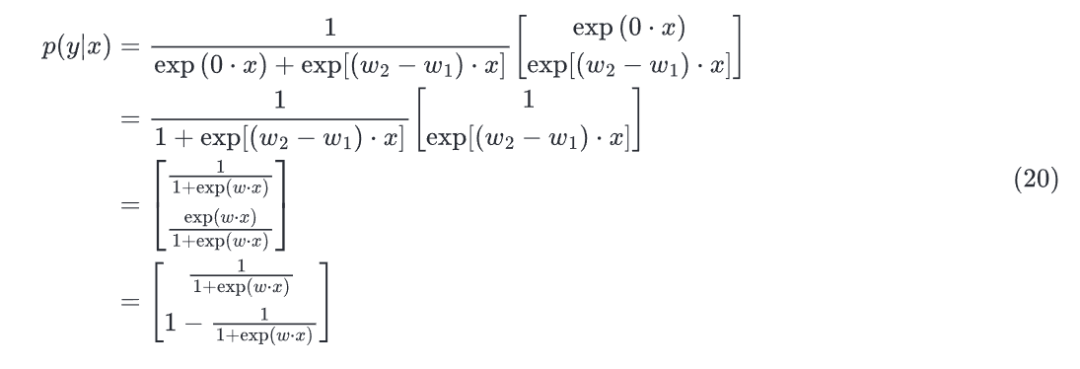
又令，得上式，整理后的式子与逻辑回归一致。

因此，多元逻辑回归实际上是逻辑回归在多分类下的一种推广。