TypeScript 4.3 新功能的实践应用
本文通过解决在实际工作中遇到的问题,层层剖析解法,带你了解 TS4.3 的高级特性,一起来看看吧。
已经成为前端标配的 TypeScript 在 5 月底发布 4.3 版本。作为一个小版本迭代,粗看并没有什么令人惊艳的新功能。但如果你真的有在持续关注 TypeScript,那么其中的一项更新值得重点关注:
Template String Type Improvements
为什么值得注意呢?看一下 TS 4.0 以来的三条更新记录:
4.0 版本新增 Variadic Tuple Types
4.1 版本新增 Template Literal Types
4.3 版本完善 Template Literal Types
然后我现在告诉你,Tuple Types 和 Template Literal Types 其实是一对关系密切的好哥们。所以,聪明的你是不是已经猜到,既然 TS 在 Tuple Types 和 Template Literal Types 持续发力,那很大概率,现在应该可以用它们来完成一些以前不太可能完成的事情。
而我呢,早在 4 月份的时候就发现了 TS 4.3 将要发布的这个新功能,并且已经在预览版中亲身体验,解决了一个非常有趣的小问题:如何将对象类型的所有可能的合法路径静态类型化。
下面就让我带你看看 4.3 增强之后的 Template Literal Types 可以解决一个什么样的真实问题吧。
还原问题现场
我们团队现在的项目中使用 FinalForm 管理表单状态,但这不是重点,重点是其中一个和 lodash set 方法几乎一模一样的 change 方法,做不到完全的类型安全。这导致我们在写相关的 TS 代码时,只能用稍显丑陋的 as any 逃生。具体示例看 👇 的代码:
type NestedForm = {
name: ['赵' | '钱' | '孙' | '李', string];
age: number;
articles: {
title: string;
sections: string[];
date: number;
likes: {
name: [string, string];
age: number;
}[];
}[];
}
// FinalForm 中的一个常用 API,语义和 lodash 中的 set 几乎一样
interface FormApi<FormValues = Record<string, any>> {
change: <F extends keyof FormValues>(name: F, value?: Partial<FormValues[F]>) => void
}
const form: FormApi<NestedForm> = // 假装有了一个 form 实例
// 基本使用
form.change('age', '20') // 这样是类型安全的
// 可大量的真实使用场景其实类型不安全,但又完全合情合理,所以只能使用 as any 逃生
form.change('name.0', '刘')
form.change('articles.0.title', 'some string')
form.change('articles.0.sections.2', 'some string')
// 项目中逃生代码
<Select
placeholder="请选择类型"
onChange={Kind => {
// 清空其他字段, 只保留 Kind
form.change(`${field}.Env.${i}` as any, { Kind });
}}
>
所以问题就是:我们能让类似的方法完全的类型安全吗?
答案我也不藏着掖着了:解决此类问题需要 4.3 增强之后的 Template Literal Types 和 4.0 版本新增 Variadic Tuple Types,再加上一些其它早就有的高级特性。
看到这些新增和高级字眼,妥妥的一道高阶 TS 面试题 👀 有木有。而我确实也能向你保证,如果接下来的内容,你能做到既知其然,又知其所以然,TS 这关你稳过。
解决方案拆解,由浅入深
第一步:核心技术支撑
很多时候,解决方案往往已经藏在问题中
name.0name.1articles.0.likes.0.agenameagearticleschange 方法类型安全的部分是对象最外层的 key:
类型不安全的部分是对象其它的嵌套路径:
我们的目标其实很清晰了:得到对象的全部可能路径。也许这依然有些模糊,但如果如果我换个说法,你或许就明白了:给你一颗二叉树,问题是从根节点出发,所有可能的路径。
但是这些和 Template Literal Types 有什么关系吗?!当然有,而且非常有。我们都知道 articles.0.likes.0.age 是字符串,但是它更是 template string type。也正是它,可以让我们在类型层面表示出一个对象的全部嵌套子路径。
第二步:Template Literal Types 搭配 Variadic Tuple Types 显奇效
这一步不要求你能全部看懂,先有个大致的概念和感觉,先让你知道,Template Literal Types 搭配 Variadic Tuple Types,再用上一些泛型技巧,可以稳稳的拿到对象的全部嵌套子路径。后面会详细介绍如何用泛型求解对象的全部嵌套子路径。
核心操作
['articles', number] => articles.${number}join
split
articles.${number}=> '['articles', number]详细操作
{ name: { firstName: string, secondName: string }, hobby: string[] }
每一个路径都是一个 tuple,所有路径就是所有 tuple 的联合 👇
['name'] | [hobby] | ['name', 'firstName'] | ['name', 'secondName'] | ['hobby', number]
tuple 可以轻松转为 template string type 👇
name|hobby|name.firstName|name. secondName|hobby.${number}然后就是如何根据 path 得到 path 对应的 value 的类型 👇
给定 name.firstName可以知道对应的 value 类型是 string给定 hobby.${number}可以知道对应的 value 类型是 string结论:template string type 与 tuple type 可以等价转换
第三步:你可能不了解的 TS 高级特性
在具体详解泛型函数之前,本节想要先介绍一些你可能不了解 TS 高级特性,如果你非常有自信,可以略过此节,直接去看后面的泛型函数,如果发现看不懂,回头再看此节也不迟。
1. 你可能不了解的 TS 类型系统
我们知道 TS 最核心的功能就是一套静态类型系统,但你真的懂 TS 类型系统吗?让我问你一个问题测试一下:TS 的类型是值的集合吗?
这是一个非常有趣的问题,正确答案是:编程语言中的类型,除了一个特例之外,确实都是值的集合。但因为特例的存在,我们就不能将编程语言中的类型视为值的集合。这个特例在 TS 中叫 never,并无对应的值,用于表示代码会崩溃退出或陷入死循环。并且,never 是所有类型的子类型,这意味着你写的任何看似被静态类型保护着的安全无忧的函数,实际运行时也都有可能崩溃或死循环。很无奈,这种没人喜欢的可能性是静态类型系统允许的合法行为。所以,静态类型也不是万能的。
2. Conditional types
At the heart of most useful programs, we have to make decisions based on input.
Conditional types help describe the relation between the types of inputs and outputs.
条件类型的引入,是 TS 泛型开始发光发热的基础。我们都知道,编程不可能离开用条件分支做决定,任何实际编程项目中,都随处可见 if else。
TS 泛型中最普通的条件分支是这个样子的:
SomeType extends OtherType ? TrueType : FalseType;
我们可以基于条件分支做一些有用事情。比如判断一个类型是不是数组类型,如果是,就返回数组的元素类型。
type Flatten<T> = T extends unknown[] ? T[number] : T;
// Extracts out the element type.
type Str = Flatten<string[]>;
// string
// Leaves the type alone.
type Num = Flatten<number>;
// number
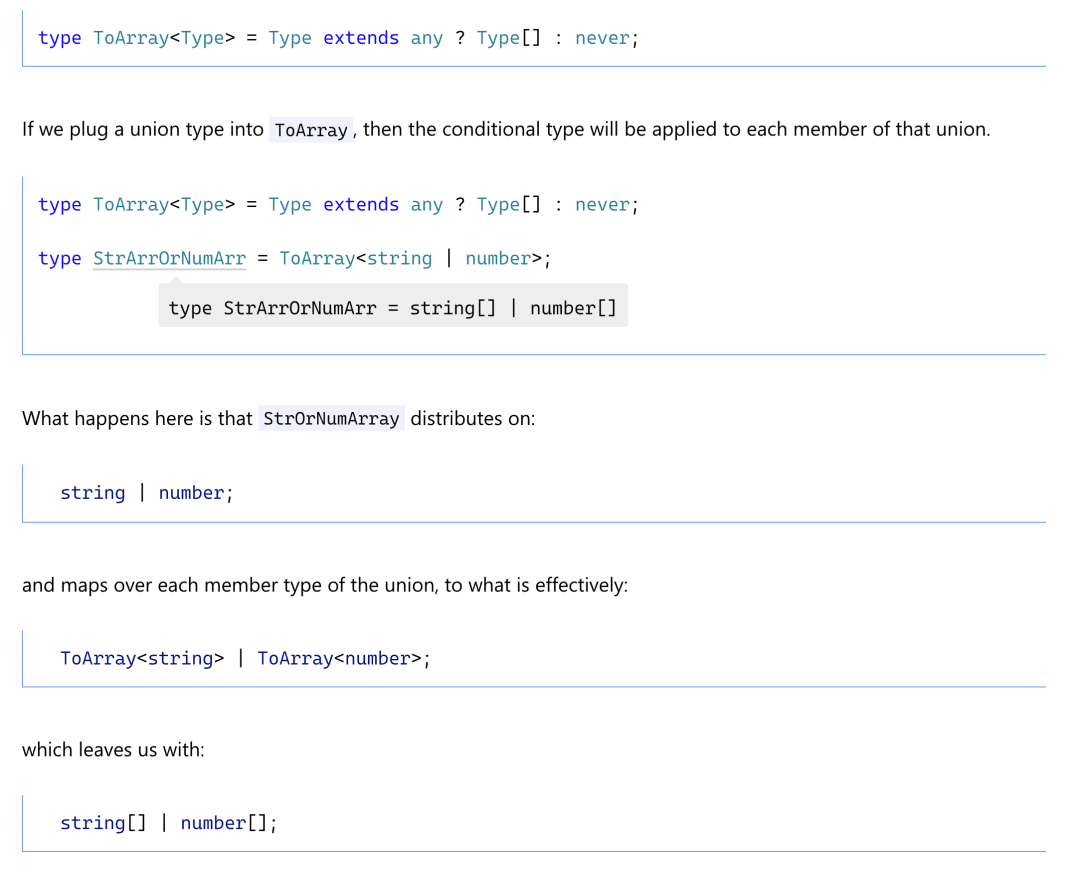
Distributive Conditional Types
When conditional types act on a generic type, they become distributive when given a union type.
编程除了用分支做决定外,还离不开循环,毕竟一个个手写是完全不现实的,TS 泛型函数并没有常规意义上的 for 或 while 循环,但却有 Distributive Conditional Types,其作用非常类似数组的 map 方法,只不过是作用对象是 union 类型而已。具体表现可以直接看下面的图示:
3. Inferring Within Conditional Types
关于条件类型还有一个不可缺失的高阶特性:infer 推断。TS 的 infer 能力可以让我们使用声明式的编程方法从一个复杂复合类型中精准提取出我们感兴趣的那部分。
Here, we used the
inferkeyword to declaratively introduce a new generic type variable namedIteminstead of specifying how to retrieve the element type ofTwithin the true branch.
例如上面提取数组元素类型的泛型可以用 infer 实现如下,看上去是不是更简洁省劲一些呢?
type Flatten<Type> = Type extends Array<infer Item> ? Item : Type;
4. 元组 tuple 和模版字符串类型 template string type 的递归操作
这一小节之前的内容都只算热身,这一小节的递归泛型是本文核心。解决方案拆解的第一步已经指出核心技术支撑是 Variadic Tuple Types 和 Template Literal Types。这一小节将在条件泛型和 infer 的基础上引入 tuple 和 template string 的递归操作。
Tuple 就是 length 固定,每一个元素类型也固定的 Array,如下面代码所示,Test1 是一个 tuple,length 固定为 4,每一个元素类型也固定。JoinTupleToTemplateStringType 是一个泛型函数,可以将一个 Tuple 转换为 Template Literal Types,作用到 Test1 上得到的结果是 names.${number}.firstName.lastName。具体到 JoinTupleToTemplateStringType 的实现,除了条件类型和 infer 的使用,我们还使用了一个威力巨大的 TS 泛型特性:递归。如果对算法略有了解,会知道任何算法操作的核心是分支和循环,而循环又何递归完全等价,意思是任何用循环实现的算法,理论上都可以用递归实现,反之亦然。在目前主流编程语言中,绝大部分都是以循环为主,甚至很多人可能听过一些「不要写递归」之类的说法。但在 TS 泛型层面,我们只能使用递归和条件来实现一些有趣的泛型函数。下面的代码我加了详细的注释,顺着慢慢看,别害怕,就一定能看懂。因为递归有一个特点,写起来可能不容易,但阅读的时候往往要容易很多(前提是单个逻辑完整且不存在嵌套的递归)。
type Test1 = ['names', number, 'firstName', 'lastName'];
// 假设需要处理的 Tuple 元素类型只会是字符串或 number
// 做这个假设的原因是,对象 object 的 key 一般来说,只会是 string 或 number
type JoinTupleToTemplateStringType<T> = T extends [infer Single] // 此处是递归基,用于判断 T 是否已经是最简单的只有一个元素的 Tuple
? Single extends string | number // 如果是递归基,则提取出 Single 的具体类型
? `${Single}`
: never
// 如果还未到递归基,则继续递归
: T extends [infer First, ...infer RestTuple] // 完全类似 JS 数组解构
? First extends string | number
? `${First}.${JoinTupleToTemplateStringType<RestTuple>}` // 递归操作
: never
: never;
type TestJoinTupleToTemplateStringType = JoinTupleToTemplateStringType<Test1>;
在上面的递归操作里,是把 Tuple 转换成 Template Literal Type,下面这个递归泛型相反,是把一个 Template Literal Type 转换成 Tuple。代码也加了详细注释,别害怕,只要慢慢看,就一定能看懂。
type Test2 = `names.${number}.firstName.lastName.${number}`;
type SplitTemplateStringTypeToTuple<T> =
T extends `${infer First}.${infer Rest}`
// 此分支表示需要继续递归
? First extends `${number}`
? [number, ...SplitTemplateStringTypeToTuple<Rest>] // 完全类似 JS 数组构造
: [First, ...SplitTemplateStringTypeToTuple<Rest>]
// 此分支表示抵达递归基,递归基不是 nubmer 就是 string
: T extends `${number}`
? [number]
: [T];
type TestSplitTemplateStringTypeToTuple = SplitTemplateStringTypeToTuple<Test2>;
最后一步:求解对象全部嵌套子路径的递归泛型
终于到了最后一步,真正的解决方案,一个求解对象全部嵌套子路径的递归泛型 AllPathsOf。AllPathsOf 并不复杂,由两个嵌套泛型构成,这两个嵌套泛型分别只有七八行,加起来十五行,是不是还行?所以问题最关键的一步是想到先求出 TuplePaths,再铺平。其中铺平这一步我们之前已经展示过,就是用一个递归泛型把一个 Tuple 转换成 Template Literal Type。所以问题只剩下一个:如何把对象的所有子路径提取并表示为 Tuple Union。RecursivelyTuplePaths 本身也不复杂,下面代码中有详细注释,别害怕,慢慢看,一定能看懂。
剩下就是的 ValueMatchingPath,看代码好像比 AllPathsOf 还复杂一点,但由于只是附加功能,此处不详细介绍,感兴趣的可以看代码,相信经过前面几轮递归泛型的洗礼,这个稍微长一点的也不成问题。
//
// 支持的环境:TS 4.3+
//
/** 获取嵌套对象的全部子路径 */
type AllPathsOf<NestedObj> = object extends NestedObj
? never
// 先把全部子路径组织成 tuple union,再把每一个 tuple 展平为 Template Literal Type
: FlattenPathTuples<RecursivelyTuplePaths<NestedObj>>;
/** 给定子路径和嵌套对象,获取子路径对应的 value 类型 */
export type ValueMatchingPath<NestedObj, Path extends AllPathsOf<NestedObj>> =
string extends Path
? any
: object extends NestedObj
? any
: NestedObj extends readonly (infer SingleValue)[] // Array 情况
? Path extends `${string}.${infer NextPath}`
? NextPath extends AllPathsOf<NestedObj[number]> // Path 有嵌套情况,继续递归
? ValueMatchingPath<NestedObj[number], NextPath>
: never
: SingleValue // Path 无嵌套情况,数组的 item 类型就是目标结果
: Path extends keyof NestedObj // Record 情况
? NestedObj[Path] // Path 是 Record 的 key 之一,则可直接返回目标结果
: Path extends `${infer Key}.${infer NextPath}` // 否则继续递归
? Key extends keyof NestedObj
? NextPath extends AllPathsOf<NestedObj[Key]> // 通过两层判断进入递归
? ValueMatchingPath<NestedObj[Key], NextPath>
: never
: never
: never;
/**
* Recursively convert objects to tuples, like
* `{ name: { first: string } }` -> `['name'] | ['name', 'first']`
*/
type RecursivelyTuplePaths<NestedObj> = NestedObj extends (infer ItemValue)[] // Array 情况
// Array 情况需要返回一个 number,然后继续递归
? [number] | [number, ...RecursivelyTuplePaths<ItemValue>] // 完全类似 JS 数组构造方法
: NestedObj extends Record<string, any> // Record 情况
?
// record 情况需要返回 record 最外层的 key,然后继续递归
| [keyof NestedObj]
| {
[Key in keyof NestedObj]: [Key, ...RecursivelyTuplePaths<NestedObj[Key]>];
}[Extract<keyof NestedObj, string>]
// 此处稍微有些复杂,但做的事其实就是构造一个对象,value 是我们想要的 tuple
// 最后再将 value 提取出来
// 既不是数组又不是 record 时,表示遇到了基本类型,递归结束,返回空 tuple。
: [];
/**
* Flatten tuples created by RecursivelyTupleKeys into a union of paths, like:
* `['name'] | ['name', 'first' ] -> 'name' | 'name.first'`
*/
type FlattenPathTuples<PathTuple extends unknown[]> = PathTuple extends []
? never
: PathTuple extends [infer SinglePath] // 注意,[string] 是 Tuple
? SinglePath extends string | number // 通过条件判断提取 Path 类型
? `${SinglePath}`
: never
: PathTuple extends [infer PrefixPath, ...infer RestTuple] // 是不是和数组解构的语法很像?
? PrefixPath extends string | number // 通过条件判断继续递归
? `${PrefixPath}.${FlattenPathTuples<Extract<RestTuple, (string | number)[]>>}`
: never
: string;
/**
* 借助 TS 4.3 的新能力(template string type 增强)改造 FormApi interface 中的 change 方法,可用性几乎完美
* */
interface FormApi<FormValues = Record<string, any>> {
change: <Path extends AllPathsOf<FormValues>>(
name: Path,
value?: Partial<ValueMatchingPath<FormValues, Path>>
) => void;
}
// 演示用的嵌套 Form 类型
interface NestedForm {
name: ['赵' | '钱' | '孙' | '李', string];
age: number;
articles: {
title: string;
sections: string[];
date: number;
likes: {
name: [string, string];
age: number;
}[];
}[];
}
// 假装有了一个 NestedForm 类型表单实例的 change 方法
const change: FormApi<NestedForm>['change'] = (name, value) => {
console.log(name, value);
};
// 👇 尽情尝试
let index = 0;
change(`articles.0.likes.${index}.age`, 10);
change(`name.${index}`, '刘'); // 其实此处依然不够安全,可以想想怎么更安全 🤔
/** 提取出来的全部子路径,放在这里直观展示一下 */
type AllPathsOfNestedForm =
| keyof NestedForm
| `name.${number}`
| `articles.${number}`
| `articles.${number}.title`
| `articles.${number}.sections`
| `articles.${number}.date`
| `articles.${number}.likes`
| `articles.${number}.sections.${number}`
| `articles.${number}.likes.${number}`
| `articles.${number}.likes.${number}.name.${number}`
| `articles.${number}.likes.${number}.age`
| `articles.${number}.likes.${number}.name`;
最最后一步:使用尾递归技术优化泛型函数的性能
最最后一步是个 bonus,额外的优化。可以看到前面的 AllPathsOf 是个运行复杂度不低的递归。这应该是递归的通病,也有一些朋友因为这个不喜欢递归。但其实递归的这种问题是可以通过技术手段规避掉的。这个技术手段就是尾递归。
下面我们用经典的 fibonacci 数列来切实感受一下递归、尾递归、循环的区别:
// 递归版 fibonacci,性能捉急,简直不可容忍
function fibRecursive(n: number): number {
return n <= 1 ? n : fibRecursive(n - 1) + fibRecursive(n - 2);
}
// 尾递归版 fibonacci,化腐朽为神奇,性能飙升
function fibTailRecursive(n: number) {
function fib(a: number, b: number, n: number): number {
return n === 0 ? a : fib(b, a + b, n - 1);
}
return fib(0, 1, n);
}
// 循环版 fibonacci,好像和尾递归版异曲同工?
function fibLoop(n: number) {
let [a, b] = [0, 1];
for (let i = 0; i < n; i++) {
[a, b] = [b, a + b];
}
return a;
}
是的,尾递归的性能在时间复杂度上和循环一样一样的。
下面看看尾递归如何在 TS 泛型中使用:
type OneLevelPathOf<T> = keyof T & (string | number)
type PathForHint<T> = OneLevelPathOf<T>;
// P 参数是一个状态容器,用于承载每一步的递归结果,并最终帮我们实现尾递归
type PathOf<T, K extends string, P extends string = ''> =
K extends `${infer U}.${infer V}`
? U extends keyof T // Record
? PathOf<T[U], V, `${P}${U}.`>
: T extends unknown[] // Array
? PathOf<T[number], V, `${P}${number}.`>
: `${P}${PathForHint<T>}` // 走到此分支,表示参数有误,提示用户正确的参数
: K extends keyof T
? `${P}${K}`
: T extends unknown[]
? `${P}${number}`
: `${P}${PathForHint<T>}`; // 走到此分支,表示参数有误,提示用户正确的参数
/**
* 使用尾递归泛型改造 FormApi interface 中的 change 方法,提升性能
* */
interface FormApi<FormValues = Record<string, any>> {
change: <Path extends string>(
// 此处按需判断给定的 name 参数是否是 FormValues 的子路径
// 编译性能会有明显提升
name: PathOf<FormValues, Path>,
value?: Partial<ValueMatchingPath<FormValues, Path>>
) => void;
}
结语
TS 4.3 Template Literal Types 实践到这里就结束了。这些略有复杂但逻辑清晰的递归泛型理解起来肯定有一些难度,如果实在看不懂,也没关系。后面可以慢慢来。但想要真正掌握 TS,这个程度的递归泛型是必须要掌握的,所以本文的确还是有一些价值的 👀 😊。
参考链接
https://github.com/microsoft/TypeScript/issues/20423
